Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 20

Зависимость электропроводности полупроводника от температуры определяется не только через μ(T), но благодаря зависимости п(Т), имеющей для собственного полупроводника вид  где ε_g— ширина запрещенной зоны. Следовательно, получаем

                                     (3.100)

Поскольку ε_g>>kT то при умеренных температурах множитель Т^3/(2+νν) меняется сущестпепно медленнее, чем ехр(—ε_g /k_BT). k образом, можно приближенно записать

                                                           (3.101)

На рис.  3.6 приведены   схематические   зависимости   n=n(1/T)

Рис. 3.

Сплошная кривая  относится  к собственной  проводимости штриховая—к  примесной,    а  область   штрихпунктирная - «выморажинапию» проводимости [6].

Дрейфовые и диффузионные токи.  Соотношение Эйнштейна

Рассмотрим   теперь неоднородные   полупроводники,   концентрации носителей   в которых   меняются   в   пространстве, т. е. п () и р(). В этом случае будет происходить процесс выравнивания концентраций (диффузия носителей), причем диффузионные потоки электронов и дырок есть

(3.102)

(3.103)

где  D_p— соответственно коэффициенты диффузии электронов и дырок. Диффузионный ток , возникший из-за градиента концентраций носителей, приведет к пространственному разделению заряда, поскольку, согласно

(3.102) и (3.103), и направлены в разные стороны. Разделение зарядов приведет к появлению электрического поля, которое заставит дрейфовать носители. Вычислим полную плотность тока в неоднородном полупроводнике. Дрейфовые составляющие тока при наличии электрического поля Е имеют вид

(3.104)

Складывая дрейфовые составляющие с диффузионными, получим

+=e(n+p)+e (n -p)                             (3.105)

Выражение  (3.105)  представляет собой полный ток в полупроводнике.

Существует интересное соотношение между и , D_pи . Пусть =0, тогда

=e+eDn=0

Поскольку =    (ф — электрический потенциал), то

=                                                                 (3.106)

Концентрация электронов в потенциальном .поле ф есть

n = exp 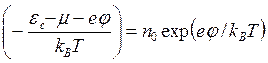                                               (3.107)

Отсюда имеем

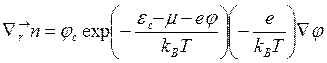                                                    (3.107)

Тогда получаем

-= -D

Следовательно, имеет место соотношение

D=                                                                                    (3.109)

Аналогично будем иметь для дырок   D=

Выражения эти связывают коэффициенты диффузии и подвижности носителей. Если теперь вспомнить раздел о диффузионном приближении в кинетике, то нетрудно увидеть, что там были получены аналогичные соотношения, носящие название соотношений Эйнштейна. Фактически полученные ранее выражения содержат, как частный случай, и пример полупроводников. Вместе с тем, в полупроводниках соотношения играют важное значение, позволяя оценивать, например, подвижность, измеряя коэффициент диффузии и т. д,

Приведем оценку D. При T=3ООК величина kT/e~ ~25,9-10^-3 В, поэтому при ≈10³ см²/(В·с) имеем D~ 25,9 см²/(В·с)

Пусть теперь полный ток равен нулю 0, тогда из (3.105) получим выражение для амбиполярного поля

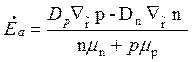(3.110)

Подставляя (3.110) в выражения для  и  и принимая, что , получаем

(3.111)

где D =— коэффициент амбшюлярной диффузии. Интересно отметить, что в примесных полупроводниках (где пр) при n>>р (полупроводник n-типа) имеем D~D_n, а в полупроводниках р-типа (р>>л) получаем D~D_n. Таким образом, Dпо порядку величины совпадает всегда с коэффициентом диффузии неосновных носителей. Рассмотренные свойства неоднородных полупроводников играют значительную роль в ряде важных физических явлений (в частности, в транзисторном эффекте [12]).

Теплопроводность и число Лоренца

Аналогично определению тока можно записать и выражение для плотности теплового потока      . Естественно, имеются и два коэффициента теплопроводности А„ и следовательные вычисления в случае, например, электронов дают (подробнее см. [6])

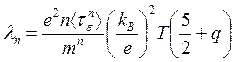                                                      (3.112)

Последнее выражение записано для невырожденных полупроводников. Теперь, воспользовавшись выражением для о„, запишем