Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 25

Теперь  рассмотрим  отдельно  случай  гальваномагнитных эффектов и термомагнитных. В случае  решение уравнения (3.139) можно искать в ви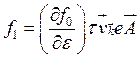де , где— неизвестный вектор,  подлежащий  определению. Можно показать, что вычисления этого вектора [5, 6] дают

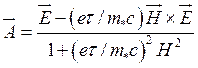             (3.142)

Отсюда нетрудно определить выражение для плотности тока носителей

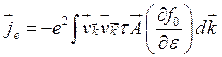     (3.143)

где вычисляется по (3.141). Из выражения (3.142) можно получить обобщенный закон Ома

        (3.144)

Здесь  — тензор электропроводности в магнитном поле; 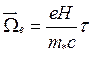 —параметр Холла . В случае наличия в образце температурного градиента уравнение (3.143) обобщается и принимает вид [6]

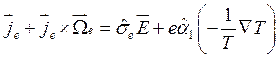     (3.145)

где α₁ — тензор, выражаемый через дифференциальную термо-ЭДС и другие параметры [6, 111. Аналогичное (3.142) соотношение можно получить и для потока тепла

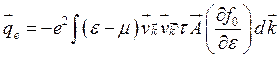     (3.146)

Тогда для потока тепла имеем

       (3.147)

где — тензор теплопроводности; — тензор, определяемый в [6]. Заметим, что при наличии магнитного поля соотношения (3.77) можно обобщить и они примут ;вид

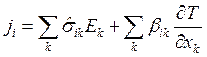          (3.148)

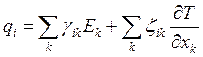
Заметим, что величины о«, р_л, y_ikи g_ift становятся теперь тензорными, однако между ними можно установить определенную связь, аналогичную связи между величинами а„ р_е, у, и g_e в (3.77) [11]. Сделаем еще несколько замечаний относительно (3.147). Из принципа симметрии кинетических коэффициентов   (принцип Онзагера   [11])  следует, что . Из этого же принципа можно найти связи вида .и т. д. [11]. Кроме того, как можно показать [11], между компонентами тензоров электропроводности и теплопроводности имеет место соотношение 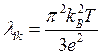, т.  е.   выполняется   закон    Видемана — Франца (заметим, что это, естественно, справедливо лишь для упругих столкновений) . К сожалению, мы здесь не имеем возможности обсудить ряд важных физических эффектов, следующих из (3.147) (см. [6, 11, 14]).

4.3. Гальваномагнитные явления

В присутствие магнитного поля, 'как мы видели, движение зарядов происходит по-разному в различных направлениях. Это приводит к тому, что в магнитном поле появляется специфическая анизотропия свойств твердых тел. Эффекты, появляющиеся при этом в случае , как отмечено выше, носят название гальваномагнитных. Важнейшими среди них являются эффект Холла и изменение сопротивления в магнитном поле, магнетосопротивление. На двух последних эффектах остановимся подробнее. Что касается термомагнитных явлений, то их изложение можно найти в [13, 6].

Слабые магнитные поля

Сначала рассмотрим случай слабых магнитных полей. Здесь полученные результаты аналогичны соответствующим результатам для свободных носителей (например, в газовой плазме). Далее будут исследованы вопросы о Влиянии на эффект Холла и магнетосопротивление геометрии электронных траекторий (замкнутого они или открытого типа) и соотношения между концентрацией носителей различного типа.

Эффект Холла состоит в появлении в твердом теле, помещенном в магнитное поле, компоненты электрического поля, не совпадающего по направлению с приложенным. Дадим простую физическую картину этого явления (рис. 4.2). Если

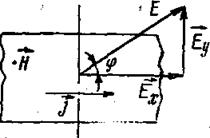
Рис. 4.2

плотность тока направлена вдоль оси х, а магнитное поле вдоль оси z, то в отсутствие магнитного поля электрическое по направлению совпадает с направлением . При включении поля появляется составляющая электрического поля вдоль оси у (это и есть поле Холла), если вдоль у ток протекать не может. Появление поля Холла указывает на изменение характера движения зарядов в магнитном поле, прячем, как показывает опыт, поле Холла есть

             (3.149)

где величина R—коэффициент пропорциональности, носящий название постоянной Холла. Угол, определяемый соотношением , называется углом Холла (см. рис. 4.2), и его знак, как нетрудно убедиться, зависит от знака заряда носителей тока. Так, для положительных носителей (например, дырок), условились считать ф>0, а для отрицательных (электроны) <р<0. Важно отметить, что Rи ф могут быть выражены через компоненты тензора электропроводности о,*. Для случая, изображенного на рис. 4.2, можно записать

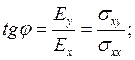
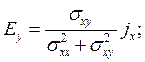
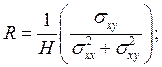      (3.150)