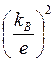Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 21

T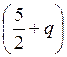=LT                                                          (3.113)

Таким образом, для невырожденных полупроводников число Лоренца Lесть функция q (см. табл. I). В случае вырожденного электронного газа, как видели выше, число Лоренца есть L=, поэтому получаем

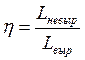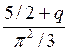=                                                                  (3.114)

При рассеянии, например, _На акустических фононак (см. табл. 1) q=—1/2, откуда η= 6/π². Таким образом, и в невырожденном полупроводнике имеет место закон Видемана—Франца, но число Лоренца зависит от механизма рассеяния.

Приведем некоторые числовые данные. Значение λ_e для Si есть 1,4 Вт/(см·К). Для сравнения укажем, что для Ag λ_e ≈ 4,33 Вт/(см·К). На рис. 3.7 представлены зависимости А,, для полупроводников. Здесь же нанесена зависимость λ_e для Сu.

Термоэлектрические явления

Найдем величину дифференциальной термо-ЭДС в полупроводниках. Для случая смешенной проводимости и-меет место формула [6]

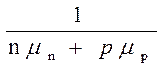
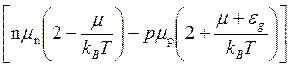                 (3.115)

В случае собственного полупроводника   (3.115)   упрощается:

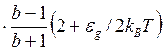                                                 (3.116)

где b = μ_n/μ_p. Для невырожденного полупроводника n-типа имеем

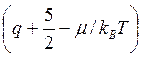-                                                             (3.117)

Сравним это выражение с формулой для металлов  (см. выше):

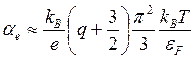                                                             (3.118)

Сравнение (3.117) и (3.118) показывает, что α>>α_e, поскольку в полупроводниках ε_g/k_BT>>1, μ>>k_BT в металлах k_BT<< ε_F. Действительно, реальные значения α_e для металлов составляют (1—10)·10^-6 В/К, а для полупроводников α≈10^-3 В/К. Тем самым термоэлектрические эффекты в полупроводниках выражены значительно Сильнее, чем в металлах. Это обстоятельство позволяет использовать полупроводники в качестве эффективных преобразователей тепловой энергии в электрическую.

3.6. Поглощение звука (электроны)

Ранее были рассмотрены механизмы поглощения звука f диэлектриках (см. главу 2), В случае металлов ситуация усложняется — основной вклад в механизм поглощения звука дают электроны. В данном разделе остановимся кратко на поглощении звука в металлах.

Поглощение звука в металлах, как показывает строгай анализ, существенно зависит от величин двух безразмерных параметров: ωτ_е и ql_e, где ω — частота звуковой волны; τ_е— время релаксация для электронов; q— волновой вектор звуковой волны (q= ω/s); l_е— длина свободного пробега для электронов. При этом важно отметить, что в силу неравенства v_F>s, ql = v/s>>, разделение звука на низкочастотный и высокочастотный требует аккуратности, поскольку, как при ωτ_е <<1, так и при ql_e <<1 возможны случаи ql_e<<1 и ql_e>>1. Рассмотрим это подробнее.

1. Низкочастотный звук (ωτ_е <<1). Для низкочастотного звука (ωτ_е <<1) возможна ситуация, когда ql_e<<1 т. е. несмотря на то, что частота звука мала по сравнению с частотой релаксации электронов, длина звуковой волны велика по сравнению с длиной свободного пробега в электронной подсистеме. В этом случае механизм поглощения звука электронами связан с изменением спектра электронов в поле волны деформации решетки (в звуковой волне). При этом электроны релаксируют в состояние равновесия, забирая часть энергии у звуковой волны. Изменение энергии звуковой волны равно в этом случае энергии, диссипируемой в электронной подсистеме. Последнюю можно записать в вид

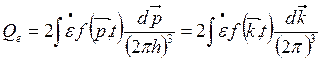(3.119)

Коэффициент затухания звука, как показано ранее, есть \=ЁЦ, где величина потока энергии в звуковой волне есть 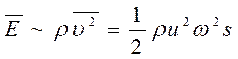. Вычисления для рассматриваемого случая (ωτ_е <<1, ql_e <<1) дают

                                           (3.120)

Отсюда получаем (I=Es)

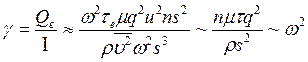(3.121)