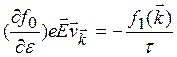Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 13

                                (3.15)

Отсюда находим  

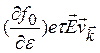= -                                   (3.16)

Плотность электрического тока, по определению, есть

                                   (3.17)

где —средняя концентрация электронов проводимости в элементе d, которая выражается через функцию распределения следующим образом:

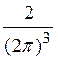
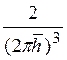
d= =                     (3.18)

Отсюда получаем

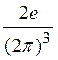
 =                                  (3.19)

Используя (3.16), находим выражение для :

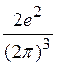
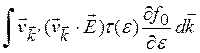 =                               (3.20)

Для вычисления .интеграла в (3.20)   можно  перейти от интегрирования по к интегрированию по dε. Такой переход осуществляется с помощью следующего приема   (подробнее см. [8, 12]). Рассмотрим закон дисперсии ε = ε(). В пространстве   выделим   поверхность,   соответствующую   условию

ε() = ε = const. Тогда вычисление   интеграла   по    будет соответствовать    интегрированию     вдоль  поверхности    S_ε:

ε() = const и интегрированию  в направлении,  перпендикулярном этой поверхности (см. рис. 3.1), т. е. будем иметь

                                   (3.21)

оде — основание элементарного цилиндра на поверхности S_ε;— изменение волнового вектора вдоль нормали к поверхностям ε() и ε() + dε() (см. рис. 3.1). Градиент функции ε() в k-пространстве также направлен вдоль нормали к поверхности ε() = const. Таким образом, можно записать, что dε = || (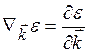) . Отсюда получаем =dS_εdε/||. Поскольку по определению, ||=|| — групповая скорость, a ε = ω, то =. Следовательно,  получаем следующее полезное соотношение:

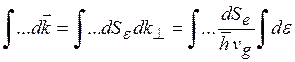                                                                        (3.22)

Величина   ν(ε) =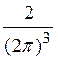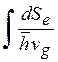-носит   название   плотности электронных состояний. Покажем, что она совпадает с величинойν(ε) введенной в первой части пособия другим способом

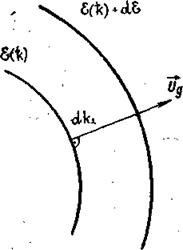
Рис. 3.1

Действительно, принимая изотропный закон дисперсии ε()==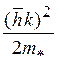, имеем

ν(ε) =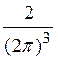 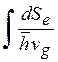=  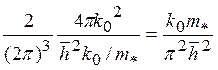                                                                                                                        (3.23)

Здесь использовано, что для изотропного закона дисперсии интегрирование по поверхности ε() = const дает ее площадь 4πk₀² (поверхность ε=const в этом случае является сферой, причем v_g=k₀/m_*). Нетрудно видеть, что (3.23) совпадает с полученным ранее (см. первую часть пособия) соотношением  ν_*(ε)=.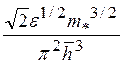

Используя (3.22), запишем (3.20) в едде

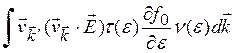 = -                                    (3.24)

Рассмотрим для конкретности случай металлов или вырожденных полупроводников, для которых возможно явное вычисление (3.24). Для равновесной функции распределения  в этом случае, как показано в первой части пособия, возможно приближенное равенство = 8(ε-μ), где 8(х) —дельта-функция. Следовательно, из (3.24) получаем закон Ома:

 = -                                    (3.25)

Таким образом, в не очень сильных полях для указанных твердых тел всегда имеет место линейная связь тока с полем (3.25). Можно записать (3.25) в виде

j_i^(e)=σ_ikE_k,(3.26)

где σ_ik носит название тензора электропроводности. Отметим, что в изотропных твердых телах, а также в кубических кристаллах величина σ_ik становится скаляром. Кроме того, если, то =v²/3, откуда находим

 = E = 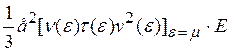                            (3.27)

Отсюда величина есть

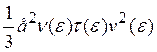                                  =                                                                                                                                                                                      (3.28)

Ниже будут проведены оценки величины электропроводности для различных механизмов рассеяния.

Теперь перейдем к рассмотрению вклада электронов в теплопроводность. В этом случае необходимо считать твердое тело неоднородно нагретым, поэтому имеем из (3,5)

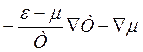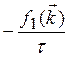() =                                                                    (3.29)

Отметим, что здесь необходимо оставить член, пропорциональный , поскольку химический потенциал μ(Т) зависит от температуры и при наличии  имеется и . Из (3.29) получаем для функции  

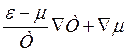 = τ(ε)()                                     (3.30)

Общее выражение для потока тепла электронов есть