Другие предметы \ Военная подготовка

Основы построения радиолокационных станций радиотехнических войск, страница 8

Понятие телесный угол вводится по аналогии с понятием угол на плоскости. Из курса геометрии известно, что угол на плоскос­ти определяется соотношением

                                                                                      (2.6)

где    — длина дуги, вырезаемая углом  на окружности с радиусом . По аналогии с выражением (2.6)

                                                                                   (2.7)

где    — площадь  участка   поверхности   сферы   с   радиусом ,

вырезаемого телесным углом .


В  соответствии с определением телесного угла  элементарный телесный угол, входящий в (2.5):

                                                                                                 (2.8)

где    — площадь  элементарной    площадки    на   поверхности

сферы с радиусом,  равным . Значение находят,   ис­пользуя рис. 2.1:

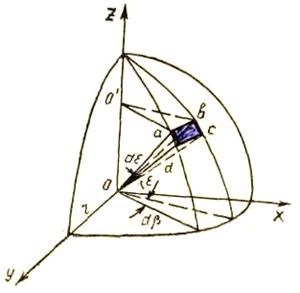
                                         (2.9)

С учетом (2.8) и (2.9)

                                          (2.10)

После подстановки в соотноше­ние (2.5) значения подынтегральной функции, найденного из (2.3), по­лучим

(2.11)      

Из (2.11) следует

Рис. 2.1. К определению  понятия пространственного угла

               (2.12)                                                                           (2.12)


Уравнение (2.12) определяет максимальную дальность дейст­вия РЛСобнаружения в режиме обзора при произвольных спо­собе обзора и форме зоны обнаружения. Из него следует, что максимальная дальность действия РЛС при заданных значениях энергии, излучаемой в зону за время однократного обзора, и эф­фективной площади приемной антенны зависит от формы, зоны обзора    (функция в  сферической   системе   координат  с точностью до постоянного коэффициента определяет граничную поверхность зоны обзора) испособа просмотра зоны обзора при­емной антенной РЛС(вид функциональной зависимости  определяется способом обзора зоны).

Энергию, излучаемую в зону обзора, можно выразить через среднюю мощность излучения и время облучения цели

(2.13)


где    —средняя   мощность,   излучаемая   передающей

антенной РЛС в телесный угол диаграммы;

 —           длительность зондирующего импульса;

 —          число импульсов в пачке.

Из выражения (2.13) следует, что перераспределение энергии, излучаемой в зону обзора, возможно путем:

изменения средней мощности в процессе обзора;

изменения времени облучения целей;

выбора формы диаграммы направленности передающейан­тенны.

Конкретизируем запись уравнения (2.12) для нескольких част­ных случаев, представляющих практический интерес.

2.1.2.  Изодальностная зона обнаружения

Будем полагать, что в процессе обзора зоны антенный луч при­емной  антенны  не  изменяет своей   ширины  = 1   при . Примером РЛС, в которой выполняется это условие, является радиолокационный высотомер с механическим качанием антенны в вертикальной плоскости.

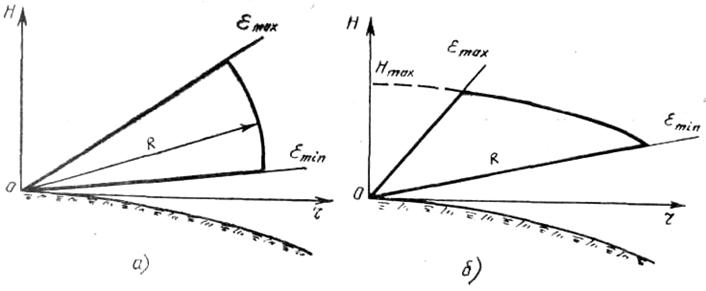
Рис.  2. 2.   Зона обнаружения:  а — изодальностная; б — изовысотная

В случае изодальностной зоны (рис. 2.2а)


( здесь — угловой  размер  зоны  обзора   в  азимутальной плоскости). Поэтому интеграл в знаменателе уравнения  (2.12)


Выразим телесный угол изодальностной зоны обнаружения  через угловые размеры зоны в азимутальной и угломестной плос­костях. Учтем для этого соотношение (2.10)

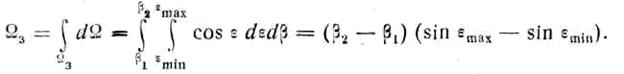
Подставляя  значениев  исходное уравнение   (2.12),  полу­чаем


2.1.3. Изовысотная зона обнаружения

Дальность до точек граничной поверхности в случае изовысотной  зоны обнаружения   (рис.  2.2б)   определяется  выражением

             (2.15)

Рассмотрим два способа формирования зоны.

1)  В процессе обзора зоны антенный луч приемной антенны не изменяет своей ширины, т. е. = 1  в пределах угловых размеров зоны. Требуемая форма зоны обнаружения в этом слу­чае может формироваться за счет изменения в угломестной плос­кости величины излучаемой средней мощности или коэффициента усиления передающей антенны по закону

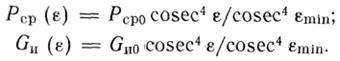
С учетом выражения (2.15)



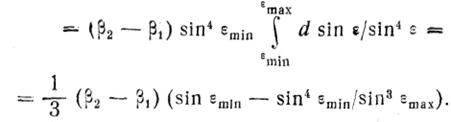
При записи формулы (2.16) учтено, что


(2.16)



Подставляя (2.16) в исходное уравнение (2.12), получаем

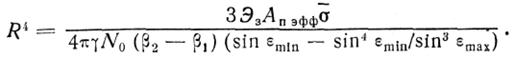 (2.17)

2) В процессе обзора зоны эффективная площадь приемной антенны изменяется в угломестной плоскости по косеканс-квад­ратному закону

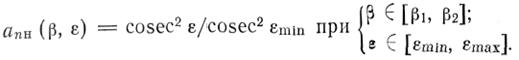               (2.18)

По такому же закону изменяется и коэффициент усиления пере­дающей антенны.

Подобное изменение эффективной площади приемной антенны и коэффициента усиления может быть обеспечено, например, за счет соответствующего выбора конфигурации зеркала антенны в вертикальной плоскости или за счет использования нескольких облучателей (приемлемое приближение к косеканс-квадратной диаграмме направленности можно получить с помощью всего лишь двух облучателей [5]).

Интеграл в уравнении (2.12) для рассматриваемого случая с учетом соотношений (2.15) и (2.18)

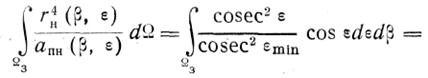
                (2.19)

и уравнение можно представить в виде

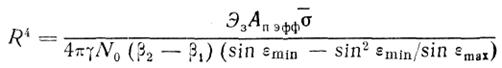 '   (2.20)

Сравним между собой рассмотренные варианты формирования изовысотной зоны по величине энергии, излучаемой в зону за вре­мя однократного обзора. При этом будем полагать, что все про­чие параметры РЛС в обоих случаях одинаковы.

Из сопоставления уравнений   (2.17)   и  (2.20)   следует

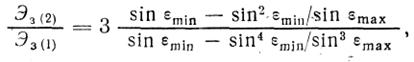
  где   — энергия, излучаемая   в зону   при   вариантах  обзора 2 и 1 соответственно.

При (на  практике это условие,  как правило,  выполняется)   записанное  выше соотношение можно  упростить:

Полученный  результатсвидетельствует,  что  с  энергетической очки  зрения  вариант   1формирования   изовысотной  зоны   пред-


Скачать файл