Другие предметы \ Военная подготовка

Основы построения радиолокационных станций радиотехнических войск, страница 12

                                    (2.50),

где

 — разность хода прямой и отраженной волн от антен­ны РЛС до цели.

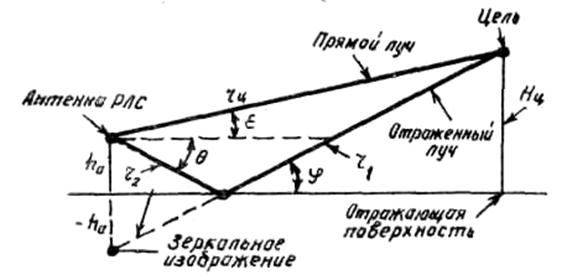
Рис.   2.4. Геометрия  отражений  от  плоской   зем­ной поверхности

В теории радиолокации маловысотными принято называть це­ли, для которых выполняется условие

поэтому с учетом выражений (2.49) и (2.50)

                                                                             (2.51)


Разность хода для плоской земной поверхности можно най­ти, пользуясь рис. 2.4:

Учитывая, что последнее выражение можно упростить:

Из рис. 2.4 видно, что

поэтому

                                          (2.52)

Для нахождения разности хода волн с учетом кривизны зем­ной поверхности требуется решить кубическое уравнение. В рабо­те [6] рассмотрен метод, упрощающий вычисления. Он предусмат­ривает использование в формуле (2.52) поправочного коэффици­ента , определяемого параметрами и :

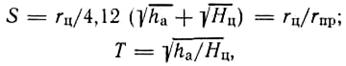
  где       —дальность до цели, км;

 — высота подъема фазового центра антенны РЛС от­
носительно  участка  земной   поверхности,   принимающего
участие в формировании отраженной волны, м;

 — высота полета цели, м;

 —            дальность прямой видимости, км.

В зависимости от величины параметров и по семейству графиков (рис. 2.5) находится поправочный коэффициент и раз­ность хода прямой и отраженной волн определяется как

                                                                         (2.53)

С учетом (2.51) и (2.53) можно записать уравнение, определя­ющее дальность обнаружения МВЦ:

                                                               (2.54)

Уравнение (2.54) является трансцендентным и его можно ре­шить либо графическим, либо итерационным методом. В случае обнаружения цели в условиях мешающих отражений от подстила­ющей поверхности, в (2.54) вместо нужно подставлять , найденное из уравнения (2.44).

Как следует из соотношения (2.54), зависимость дальности об­наружения МВЦ от технических параметров РЛС гораздо слабее, чем зависимость дальности обнаружения целей в свободном про-


странстве. Наиболее целесообразными способами увеличения даль­ности обнаружения МВЦ являются увеличение высоты подъема фа­зового центра антенны и переход на более короткие волны при одно­временном увеличении коэффициента подавленияпассивных помех.

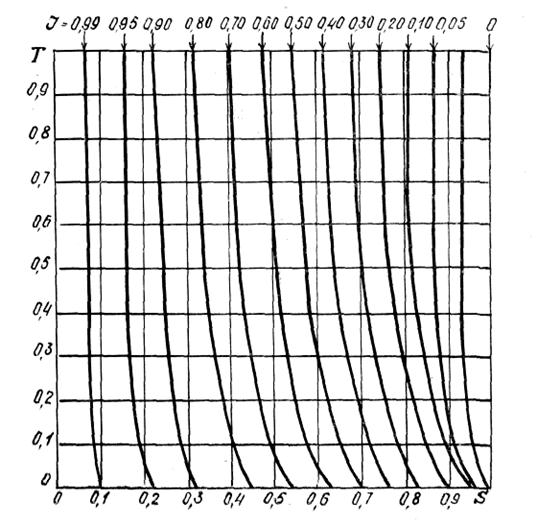
Рис. 2.5. Зависимость поправочного коэффициента от параметров и

Условия, на основании которых было получено соотношение (2.54), на практике часто не выполняются. Поэтому реальные возможности РЛС по обнаружению МВЦ должны уточняться пу­тем ее облета на малых высотах.

2.6. УПРОЩЕННЫЕ   ФОРМЫ   ЗАПИСИ   УРАВНЕНИЯ   РАДИОЛОКАЦИИ

Если дальность до цели выразить в километрах, а эффектив­ную площадь приемной антенны и эффективную поверхность це­ли — в квадратных метрах, объединить числовые значения посто­янных коэффициентов (имеются в виду коэффициенты1,38•1023 Дж/К, = 290 К, входящие в , и ), то уравне­ние радиолокации в режиме обзора будет иметь вид


где  1,99 ·10 =  — (коэффициент   1012   учитывает переход от дальности в метрах к дальности в километ­рах).

Дальнейшее упрощение предусматривает приведение уравнения к логарифмической форме и представление величин всех, парамет­ров в децибелах относительно единиц измерения, оговоренных выше

  

В каждом случае величина параметров в децибелах вычисляется как 10 значения соответствующего параметра и обозначается тем же символом, что и раньше, но заключенным в круглые скобки. Основное достоинство логарифмической формы записи уравнения радиолокации состоит в том, что она позволяет получить ответ в кратчайшие сроки при минимальной вероятности возникновения ошибок в процессе арифметических расчетов.


Глава 3.    ОСНОВНЫЕ  ХАРАКТЕРИСТИКИ             РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ

3.1. ОБЩИЕ СВЕДЕНИЯ

В активной радиолокации с пассивным ответом основными ха­рактеристиками целей являются:

среднее значение эффективной поверхности цели  (ЭПЦ)  плотность распределения вероятности ЭПЦ или плотность распределения амплитуды отраженного сигнала ;

энергетический    спектр     флюктуации    отраженного    сигнала ;

скорость движения цели и ее составляющие   (радиальная скорость , тангенциальная скорость );

линейные размеры цели ;

априорное распределение целей в пространстве.

Все перечисленные характеристики в общем случае являются статистическими [30].Без знания этих характеристик целей не­возможно решить целый ряд практически важных задач, на­пример, оценить расчетным путем боевые возможности РЛС в конкретной воздушно-помеховой обстановке или предъявить тре­бования к параметрам ее трактов и систем с достаточной точностью.

3.2. СТАТИСТИЧЕСКИЕ МОДЕЛИ ЦЕЛЕЙ

Статистические характеристики   цели и могут

быть определены по экспериментально снятой диаграмме обратно­го вторичного излучения цели. Однако подобный путь связан с большими практическими трудностями. Поэтому при определении  и в большинстве случаев реальные цели заменяют моделями, статистические, характеристики которых близки к соот­ветствующим характеристикам целей. Для уменьшения многооб­разия все цели при анализе и  синтезе РЛС  разбивают на пять видов (моделей).

Цели 1-го вида. К целям 1-го вида относятся цели без блестя­щей точки (без доминирующего отражателя) с медленными флюктуациями отраженных сигналов.

Под медленными понимают такие флюктуации, ширина спек­тра которых удовлетворяет условию

                                                                           (3.1)

  где        — время однократного обзора зоны;

  — частота повторения зондирующих импульсов.


Физическая модель — совокупность большого числа произвольно расположенных в ограниченном объеме равноценных независимых вторичных излучателей, относительная скорость перемещения ко­торых обеспечивает выполнение условия (3.1).

Плотность распределения вероятности эффективной поверхнос­ти цели  1-го вида описывается экспоненциальным  законом

Скачать файл