Рассчитаем r = 2 + 2 = 4 Ом
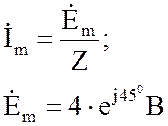 2. Запишем закон Ома в комплексной
форме, определим комплексную амплитуду э.д.с.
2. Запишем закон Ома в комплексной
форме, определим комплексную амплитуду э.д.с.
3. Рассчитаем индуктивное сопротивление
![]() Ом
Ом
4. Рассчитаем емкостное сопротивление
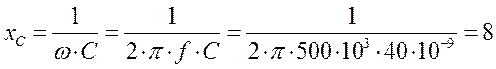 Ом
Ом
5. Рассчитаем полное комплексное сопротивление
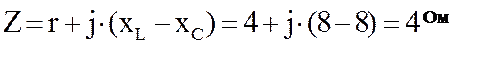
6. Рассчитаем ток в цепи
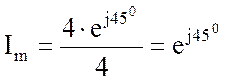 А
А
![]() А,
А,
амплитуда тока Im - 1А
7. Рассчитаем падение напряжения на сопротивлении
![]() В,
В,
![]() В.
В.
|
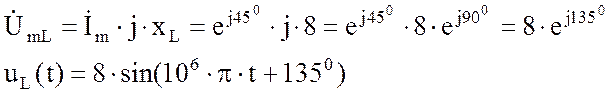 8. Рассчитаем падение напряжения на
индуктивности
8. Рассчитаем падение напряжения на
индуктивности
|
9. Рассчитаем падение напряжения на емкости
|
|
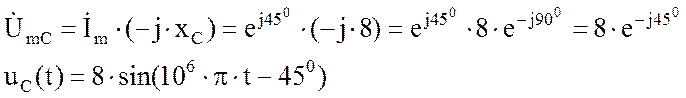
10. Определим сдвиг фаз между падением напряжения на индуктивности и падением напряжения на емкости.
![]()
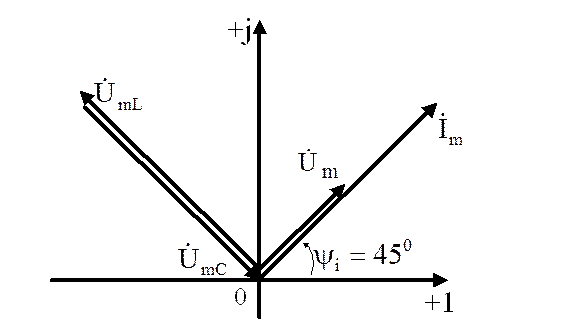 Найдем отношение амплитуды напряжения
на реактивном элементе к амплитуде э.д.с. источника
Найдем отношение амплитуды напряжения
на реактивном элементе к амплитуде э.д.с. источника
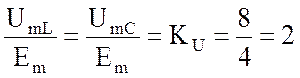 |
11.Построим векторную диаграмму
![]()
|
Определив, какой характер будет иметь r,L,C- цепь на частотах:
|
|
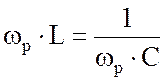 Так как на резонансной
частоте имеет место равенство
Так как на резонансной
частоте имеет место равенство
 |
и если частоту ![]() уменьшить относительно
уменьшить относительно ![]() , то при
этом
, то при
этом
 цепь будет носить активно-емкостный характер, и, наоборот,
если частоту
цепь будет носить активно-емкостный характер, и, наоборот,
если частоту ![]() увеличить относительно
увеличить относительно ![]() , то , при этом
цепь будет носить активно-индуктивный характер.
, то , при этом
цепь будет носить активно-индуктивный характер.
Подробнее этот вопрос будет рассмотрен в теме 4 "колебательные контуры”.
ПРИМЕР l.9. Для схемы изображенной на рис.1.54 определить ток в цепи, если к цепи приложено напряжение Um , построить векторную диаграмму, определить величины результирующей индуктивности и емкости.
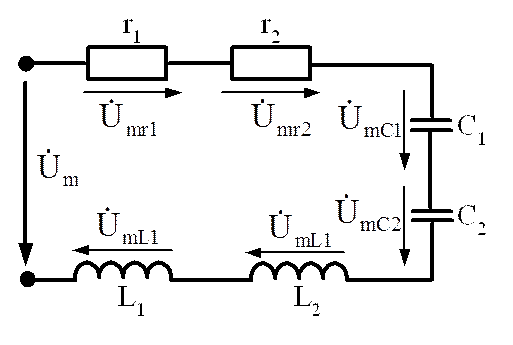
|
Решение:
Согласно второму закона Кирхгофа можно записать
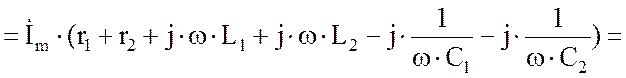
![]()
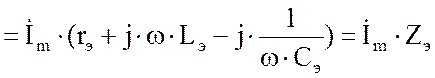 |
|||
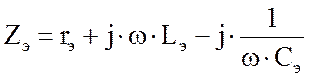 |
|||
где
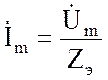 |
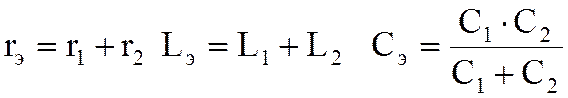 |
Причем,
Согласно этих выражений вычисляют результирующие значения элементов r , L и С при их последовательном соединении.
Выражение для С получено следующим образом
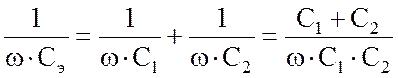
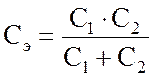 сокращая
сокращая ![]() и, вычисляя
обратные величины в левой и правой части уравнения,
получим (1.46)
и, вычисляя
обратные величины в левой и правой части уравнения,
получим (1.46)
Векторную диаграмму построим в предположении, что уже известен ток, протекающей в цепи, условно примем его начальную фазу равной нулю, тогда векторная диаграмма будет иметь вид, изображенный на рис.1.55.
Данная векторная диаграмма является условной, т.к. направление вектора
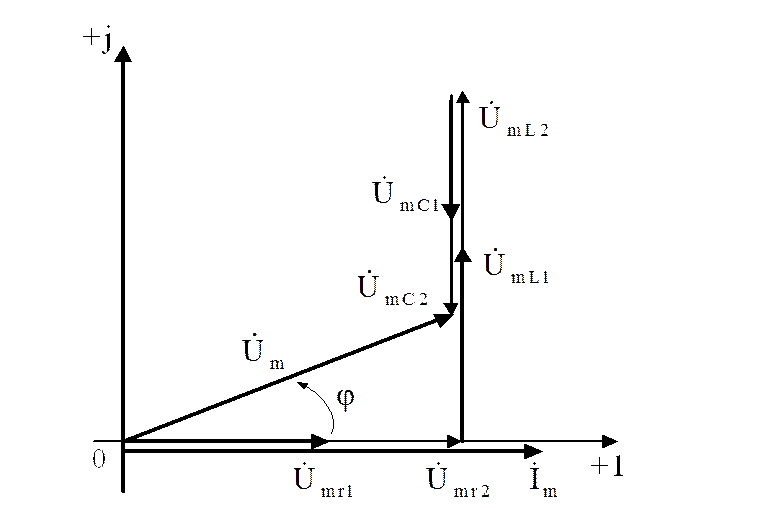
![]() , полученного в результате построения диаграммы может не совпадать с
действительным направлением этого вектора, потому что начальную фазу тока мы
условно приняли равной нулю.
, полученного в результате построения диаграммы может не совпадать с
действительным направлением этого вектора, потому что начальную фазу тока мы
условно приняли равной нулю.
Чтобы привести полученную векторную
диаграмму в соответствие с действитель
ной, следует осуществить поворот постро-
енной условной векторной диаграммы та-
![]() ким образом, чтобы вектор занял задан-
ким образом, чтобы вектор занял задан-
ное по условию задачи положение.
|
ПРИМЕЧАНИЕ:
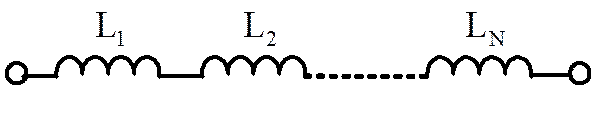 Индуктивность
цепи, изображенной на pиc.1.56, определяют согласно выражения
Индуктивность
цепи, изображенной на pиc.1.56, определяют согласно выражения
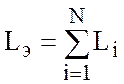
|
|
Емкость цепи, изображенную на рис. 1.57, определяют следующим образом
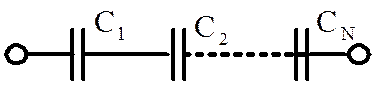 |
|||
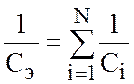 |
|||
|
ВОПРОСЫ:
1. Что называется электрической цепью?
2. В чем заключается расчет электрической цепи?
3. Сформулируйте I и II Законы Кирхгофа.
4. Что такое «резонанс напряжений»?
5. Сформулируйте признаки резонанса?
1.6.2. Цепь синусоидального тока с параллельным соединением элементов
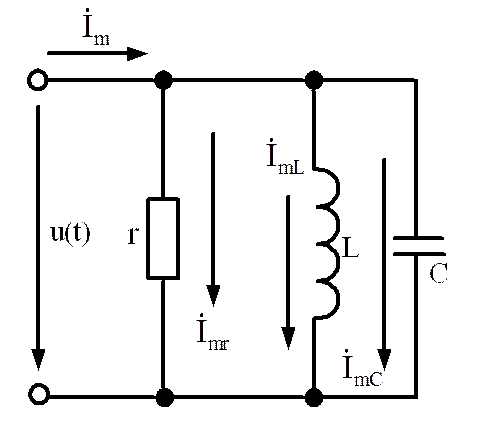 |
Если к цепи, изображенной на рис.1.58, приложить синусоидальное напряжение
![]()
|
напряжением, ток в ветви с
индуктивностью ![]() отстает по фазе от приложенного напряжения на
отстает по фазе от приложенного напряжения на ![]() а ток в ветви с емкостью
а ток в ветви с емкостью ![]() опережает по фазе приложенное
напряжение на
опережает по фазе приложенное
напряжение на ![]() , на основании первого закона
, на основании первого закона
Кирхгофа для мгновенных значений токов можно записать
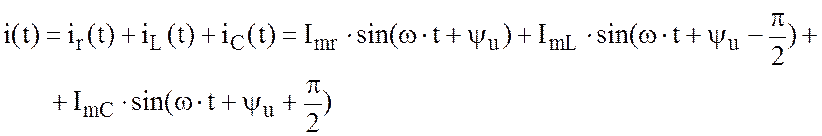 |
или в комплексной форме
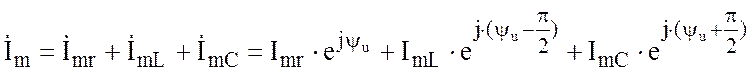 |
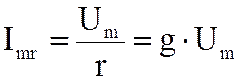 где
где
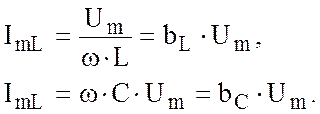 |
|
Выражение (1.49) можно записать в виде
![]()
![]()
|
Величина |
 |
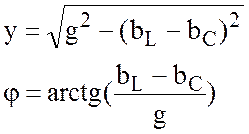
|
- аргумент комплексной проводимости.
Величина, обратная комплексной проводимости является комплексным сопротивлением
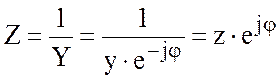 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.