Это значение тока иногда называют средневыпрямленным.
1.4.2. Формы представления синусоидальных величин
Представление синусоидальных величин проекциями вращающегося вектора
Синусоидальные величины, имеющие угловую частоту ω, можно изображать векторами, вращающимися с угловой скоростью ω, причем длина вектора в соответствующем масштабе определяется амплитудой тока (э.д.с, напряжения). В отличие от механики эти векторы не означают направления действия величины!
Для представления тока построим из начала координат радиус вектор, модуль которого равен амплитуде тока, под углом к горизонтальной оси X. Будем обозначать такой вектор Im, Um, Em. (рис.1.36)
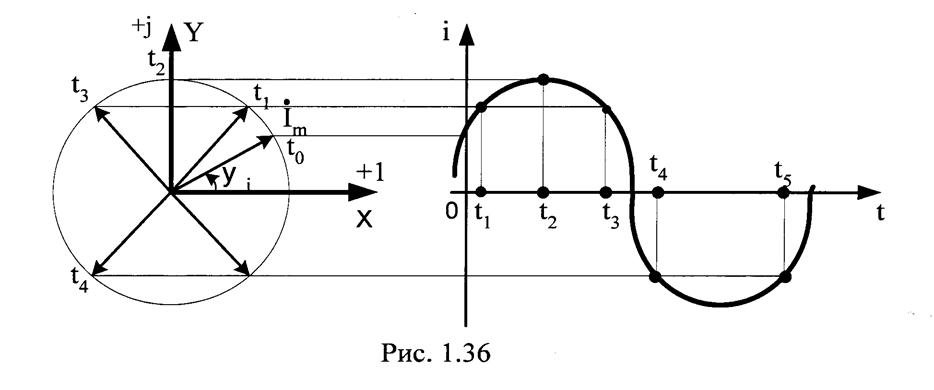 |
Значение проекции вектора на вертикальную ось - Imsinψi - значение тока в момент t = 0.
Приведем вектор во вращение против часовой стрелки с угловой скоростью ω. Полный оборот совершается за время, равное Т.
![]() В этом
случае проекция вращающегося вектора на вертикальную ось равна в избранном
масштабе мгновенному значению тока -
В этом
случае проекция вращающегося вектора на вертикальную ось равна в избранном
масштабе мгновенному значению тока -
Рядом с окружностью, описываемой концом вектора можно построить развернутую диаграмму (рис. 1.36).
Использование векторов особенно наглядно, если необходимо изобразить несколько синусоидальных величин с разными начальными фазами. Если все величины имеют одинаковую частоту ω, то важны только амплитуды и сдвиг фаз между величинами. Вращение радиусов векторов можно не изображать.
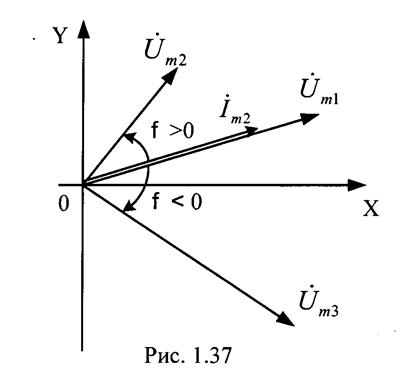 Совокупность неподвижных векторов изображающих
синусоидальные токи, э.д.с, напряжения одной частоты в начальный момент времени
называется векторной диаграммой.
Совокупность неподвижных векторов изображающих
синусоидальные токи, э.д.с, напряжения одной частоты в начальный момент времени
называется векторной диаграммой.
Сдвиг фаз между током и напряжением φ=ψu – ψi
Если φ >0, то напряжение опережает по фазе ток (ток отстает от напряжения).
Если φ <0, то напряжение отстает по фазе от тока (ток опережает напряжение).
Если φ = 0, то напряжение и ток совпадают по фазе.
Если φ = π, то напряжение и ток противоположны по фазе.
Достоинством такого представления синусоидальных величин является удобство выполнения операции сложения и вычитания.
Представление синусоидальных величин с помощью комплексных чисел
Введем на рис.1.36 комплексную плоскость. Тогда мгновенное значение синусоидальной величины можно находить, проектируя вектор тока, вращающийся с постоянной угловой скоростью ω против часовой стрелки на мнимую ось комплексной плоскости.
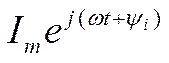 Такой
вращающийся вектор записывается в виде
Такой
вращающийся вектор записывается в виде
Таким образом, синусоидальная функция времени (ее называют оригинал) изображается комплексным числом (изображение),
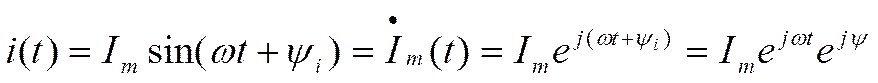 |
![]() Множитель
называется оператор вращения
Множитель
называется оператор вращения
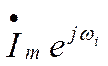 При
заданной частоте ω синусоидальная величина характеризуется двумя
вещественными числами - амплитудой Im (Um, Em) начальной фазой
yi (yu, ye), которые могло объединить в одно число
При
заданной частоте ω синусоидальная величина характеризуется двумя
вещественными числами - амплитудой Im (Um, Em) начальной фазой
yi (yu, ye), которые могло объединить в одно число
(1.29)
Комплексное число, у которого модуль соответствует амплитуде синусоидальной величины, а аргумент – начальной фазе, называется комплексной амплитудой.
![]() Так
частота синусоидальной величины обычно известна и интересуются амплитудами: и
сдвигами фаз, то множитель обычно опускают и изображают
синусоидальную величину комплексной амплитудой,
Так
частота синусоидальной величины обычно известна и интересуются амплитудами: и
сдвигами фаз, то множитель обычно опускают и изображают
синусоидальную величину комплексной амплитудой,
 |
Метод, основанный на символическом изображении действительных синусоидальных величин (функции) времени комплексными числами получил название комплексного или символического.
Расчет процессов в цепях переменного тока связан с действиями над тригонометрическими функциями, эти операций громоздки и трудоемки. С применением, символического метода достигается существенное упрощение расчетов. За счет их алгебраизации ясно, что действия над, числами проще, чем действия над функциями.
При использовании комплексного метода возникает полная аналогия записи уравнении по законам Ома и Кирхгофа и методов расчета цепей переменного тока с цепями постоянного тока.
Таким образом можно сделать вывод, что основными формами представления синусоидальных величин являются:
1. Аналитическое выражение
2. Развернутая диаграмма
3. векторная диаграмма
4. Комплексная амплитуда
5. Спектральная диаграмма (спектр).
Наиболее широкое применение на практике находит изображение синусоидальных величин комплексной амплитудой.
Для сокращения времени расчетов на занятии перевод комплексных чисел из алгебраической формы в показательную и обратно производится с помощью производится для преобразования формы комплексных чисел. (ТЭРЦ.Справочные материалы,ч.1.).
1.4.3. Некоторые сведения о действиях с комплексными числами и векторами. Справочные формулы.
Комплексные числа могут быть представлены в трех формах:
1. показательной;
2. тригонометрической;
3. алгебраической.
Связь между ними описывается выражениями:
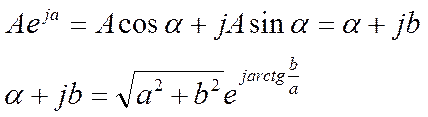 (1.30)
(1.30)
(1.31)
С комплексными числами удобно проводить следующие действия:
а) в алгебраической форме – сложение, вычитание, умножение:
(a + jb) + (c + jd) = (a + c) + j(b +d);
(a + jb) - (c + jd) = (a + c) + j(b - d);
(a + jb) · (c + jd) = a · c + jbc + jad – bd = (ac - bd) + j(bc + ad)
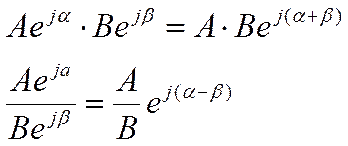 б) в показательной форме – умножение и деление:
б) в показательной форме – умножение и деление:
Другие действия с комплексными числами при проведении расчетов встречаются реже, поэтому мы их не рассматриваем.
При необходимости для проведения расчетов следует переходить от одной формы записи к другой при помощи выражении (1.30) и (1.31).
С векторами можно производить следующие действия:
а) сложение а + b = с (рис .1.38).
Рис. 1.38
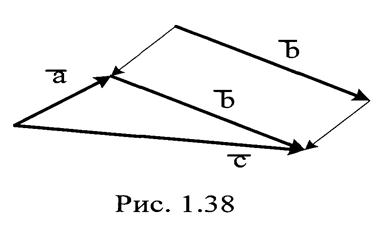 Чтобы к вектору "а", прибавить вектор "b"
необходимо переместить вектор параллельно самому себе так, чтобы начало
вектора "b" поместить в конец вектора "a".
При этом суммарный вектор будет направлен из начала вектора "а" в конец
вектора "b"
Чтобы к вектору "а", прибавить вектор "b"
необходимо переместить вектор параллельно самому себе так, чтобы начало
вектора "b" поместить в конец вектора "a".
При этом суммарный вектор будет направлен из начала вектора "а" в конец
вектора "b"
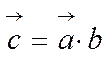 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.