Электротехника \ Радиотехнические цепи и сигналы

Линейные цепи в установившемся режиме: Курс лекций, страница 10


где  z - модуль комплексного сопротивления,

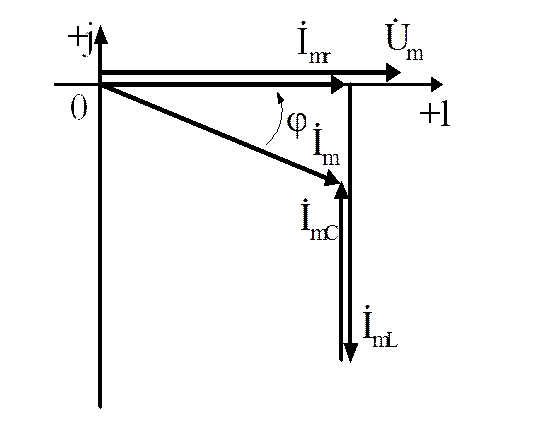
     - аргумент комплексного сопротивления цепи.

Характер цепи зависит от величины индуктивной 

 и емкостной   проводимости.   Если

а)

Рис.1.59
 
то векторная диаграмма будет иметь вид (рис. 1.59.а). Ток в неразвет-вленной части цепи отстает от прило-женного напряжения на угол, таким образом, характер цепи будет активно-индуктивным.

При  векторная диаграмма будет иметь вид,  изображенный на

(рис. 1.59б). Ток в неразветвленной части цепи будет опережать

                                            приложенное напряжение на угол    . Таким 

                                            образом характер цепи будет активно-емкост-

                                                     ным.

б)

Рис.1.59
 
 


      в)

Рис.1.59
 
Если           , то векторная диаграмма будет иметь вид (Рис.1.59.в). В этом случае ток в неразветвленной части цепи совпадает по фазе с приложенным напряжением, характер цепи является чисто активным. Рассматриваемое явление,  при котором ток в неразветвленной части цепи совпадает по фазе с приложенным напряжением, а проводимость и сопротивление цепи является чисто активной, называют резонансом токов. При таком резонансе тoки в ветвях с индуктивностью L и емкостью С могут во много раз превышать амплитуду тока в неразветвленной части цепи. Отсюда название - "резонанс токов".

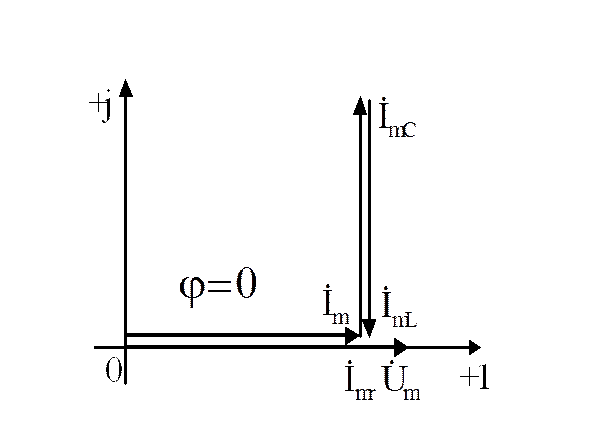
   Сравним принцип построения векторных диаграмм для схем, изображенных на pиc.l.51 и рис.1.58.

В первом случае для последовательного соединения элементов   r , L , С общей величиной для всех элементов является ток Im , протекающий через эти элементы. Поэтому под углом 0° условно откладываем вектор тока (рис.1.52).

Во втором случае для параллельного соединения элементов r , L , С общей величиной для всех элементов является напряжение         , приложенное ко всем элементам. Поэтому под углом 0° условно откладываем вектор напряжения      (рис. 1.59).

Векторные диаграммы,  изображенные на рис.1.59 являются условными,  т.к. направление вектора полученного тока может не  совпадать  с действительным его направлением и для получения истинной векторной диаграммы необходимо условную векторную диаграмму повернуть вокруг точки начала координат до совпадения полученного вектора     с истинным направлением.

 


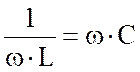Проводимости                    и                    при изменении  частоты будут изменяться,  при этом  на некоторой частоте будет иметь место равенство


в этом случае легко определить резонансную частоту

 


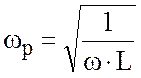(1.50)

ПРИМЕР  1.10.    Определить какой характер будет иметь параллельная r,L,C - цепь на частотах:


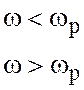а)
б)

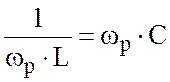Решение:

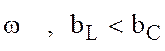
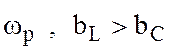Так как на резонансной частоте                            ,то при уменьшении         относительно                          ,  т.е. цепь будет иметь активно-индуктивный характер, а при увеличениях                          ,т.е. цепь будет иметь активно-емкостный характер.

ПРИМЕР  1.11.    Определить комплексную проводимость цепи, изображенную на рис.1.60 и построить один из вариантов векторной диаграммы.


Решение:

Определим комплексную проводимость цепи

где

 


                              


 


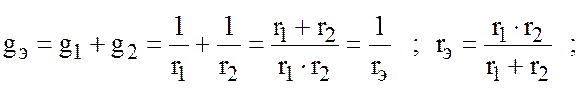(1.51)

*
 


**
 

(1.52)
 

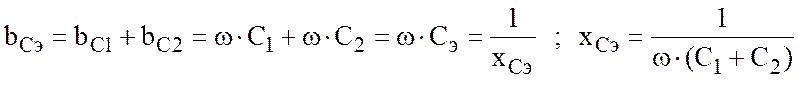Выражения,  отмеченные (*) и (**), позволяют определить эквивалентные индуктивность и емкость при параллельном соединении двух индуктивностей или емкостей.

(рис.1.59).

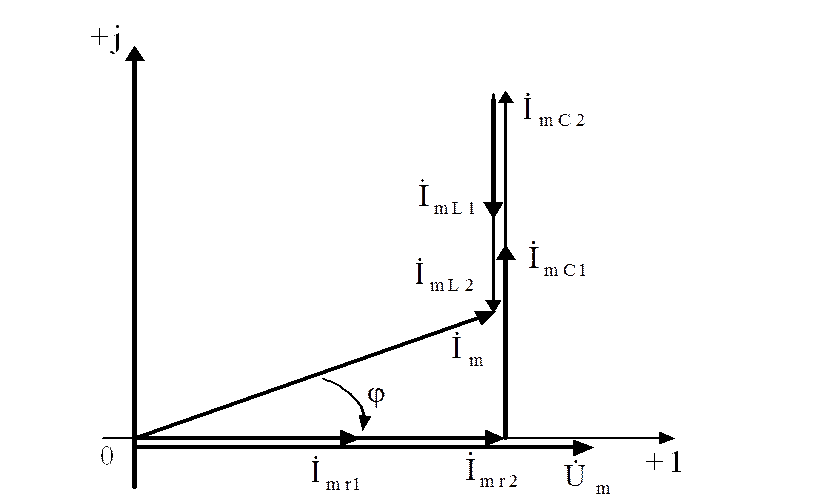
Построим векторную диаграмму для случая

Рис.1.61
 


ПРИМЕЧАНИЕ: для схемы, изображенной на рис.1.62 эквивалентная индуктивность может быть определена по формуле


(1.53)
 


Рис.1.62
 



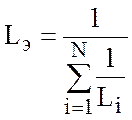для схемы, изображенной на рис.1.63   эквивалентная емкость может быть определена по формуле:

Рис.1.63
 

(1.54)
 

 


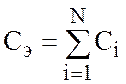Выводы :

Характер комплексного сопротивления цепи зависит от соотношения между ХL и ХС :

1. Если ХL> XС ,  то           при этой  ток будет отставать по фазе от приложенного напряжения, цепь носит активно-индуктивный характер.

2. Если ХL<ХС,  то              при этом ток будет опережать по фазе приложенное напряжение. Цепь носит активно-емкостный характер.

3. При Х=ХС сдвиг фаз     , при этом ток в цепи совпадает по фазе  с приложенным напряжением, цепь носит характер чисто активного сопротивления.

Явление в цепи синусоидального тока с последовательным соединением r, L, С,  при котором ток в цепи и приложенное к ней напряжение совпадают по фазе,  а сопротивление является чисто активным, называют резонансом напряжений.

В параллельной r, L, C цепи величина, обратная комплексной проводимости, называется комплексным сопротивлением.

Характер цепи зависит от величины индуктивной  и емкостной     

проводимости. Если , то ток в неразветвленной части цепи отстает от приложенного напряжения на угол, таким образом, характер цепи будет активно-индуктивным. При  и ток в неразветвленной части цепи будет опережать приложенное напряжение на угол, характер цепи будет активно-емкостным.

      в)

Рис.1.59
 
 Если , то в этом случае ток в неразветвленной части цепи совпадает по фазе с приложенным напряжением, характер цепи является чисто активным.

Скачать файл