 f1=5
B f2=45
B
f1=5
B f2=45
B
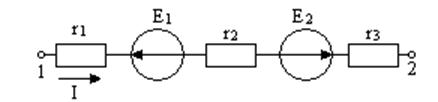
E1=5 B E2=15 B
r1=r2=r3=10 Ом
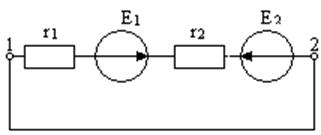
1. Выбираем УПНТ от т.1 к т.2.
2. Записываем формулу для рассматриваемого участка
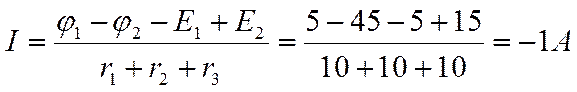 |
Знак (-) говорит о том, что ДНТ противоположно УПНТ, необходимо направление тока на схеме изменить на противоположное.
3. для направления тока от точки 2 к точке 1 формула имеет вид:
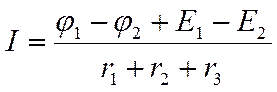 |
Закон Ома для участка цепи с пассивными элементами
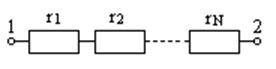 Рассмотрим участок цели с
пассивными элементами (рис.1.20).
Рассмотрим участок цели с
пассивными элементами (рис.1.20).
|
|||
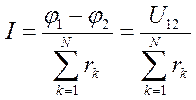 |
|||
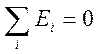 Полагаяи из(1.6)
получим (1.7)
Полагаяи из(1.6)
получим (1.7)
СЛЕДСТВИЕ. Из (1.7) следует, что эквивалентное сопротивление произвольного числа последовательно соединенных сопротивлений равно сумме этих сопротивлении.
Закон Ома для замкнутой цепи
Соединим точки 1 и 2 на схеме (рис.1.18), получим замкнутую цепь (контур). Полагая, что φ1 - φ 2 = 0 (1.6) получим:
 |
|||
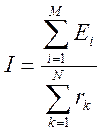 |
|||
(1.8)
|
1.3.2. Потенциальная диаграмма
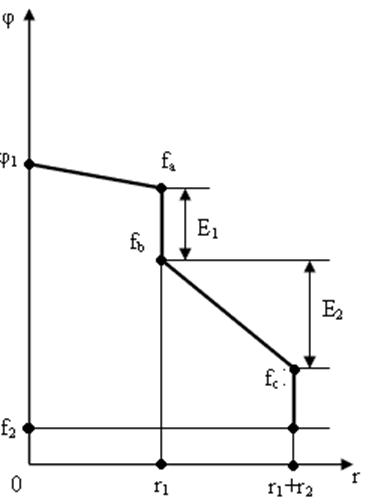
Графическое изображение распределения потенциалов вдоль электрической цепи называют потенциальной диаграммой. При построении потенциальной диаграммы по горизонтальной оси откладывают величины сопротивлении, а по вертикальной – потенциалы. При переходе через источник Э.Д.С. по направлению, совпадающего с направлением Э.Д.С., потенциал скачком возрастает на величину Э.Д.С, в противоположном случае – скачком уменьшается. При переходе через сопротивление, совпадающем с направлением тока, потенциал линейно убывает на величину падения напряжения, в противоположном случае – линейно возрастает. На рис.1.22 в качестве примера приведены потенциальные диаграммы электрических цепей, схемы которых изображены на рис.1.18 и 1.19 соответственно.
 |
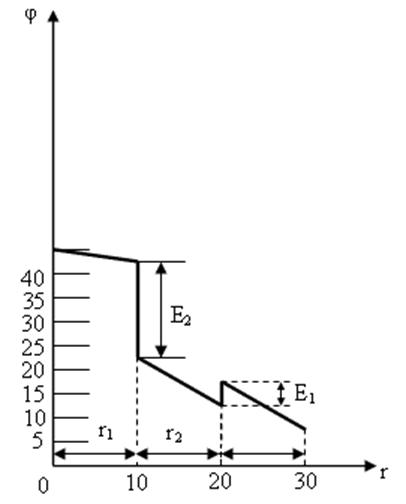 |
Рис.1.22
Иногда, при построении потенциальных диаграмм, потенциал одной из точек (f1 или f2) условно принимают равным нулю. Это значит, что график потенциальной диаграммы должен быть смещен параллельно самому себе до совпадения этой точки с горизонтальной осью.
Следует отметить, что наклон отрезков прямых, изображающих падения напряжения на сопротивлениях в одних и тех же ветвях, одинаков.
ПРИМЕР 1.2. В технических описаниях радиоэлектронной аппаратуры, выпускаемой промышленностью, приводят упрощенные потенциальные диаграммы, помещая информацию о распределении потенциалов в различных точках непосредственно на принципиальной схеме, как это показано на рис.1.23.
Потенциалы контрольных точек могут быть легко рассчитаны, если известны величины сопротивлений схемы и значения протекающих по ним токов.
Пусть, например, для приведенной схемы
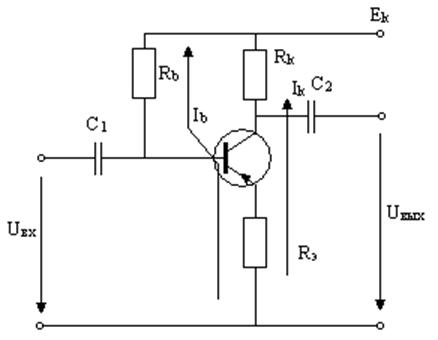
Ek=-12 В
Rк=1 кОм
Rэ=180 Ом
Rb=200 кОм
Ib=0,05 мА
Ik=5 мА
Тогда, потенциал коллектора больше потенциала шины
питания на
величину падения напряжения на сопротивлении Rк :
Потенциал базы больше потенциала шины питания на Величину падения напряжения на сопротивлении RБ:
![]() Потенциал
эмиттера меньше потенциала корпуса на величину падения напряжения на
сопротивлении за счет суммарного тока:
Потенциал
эмиттера меньше потенциала корпуса на величину падения напряжения на
сопротивлении за счет суммарного тока:
При проверке работоспособности схем осуществляют и проверку "режима работы по постоянному току", которая заключается в проверке соответствия фактического распределения потенциалов паспортным данным.
1.3.3. Законы Кирхгофа
Первый закон Кирхгофа
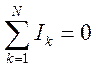 Алгебраическая
сумма токов, сходящихся в узле электрической цепи равна нулю.
Алгебраическая
сумма токов, сходящихся в узле электрической цепи равна нулю.
(1.9)
При этом токи, направленные к узлу, берут со знаков "+", a токи, направленные от узла - со знаком "-".
|
|
|

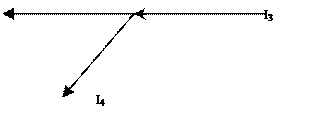 |
|||
Рис.1.24
Первый закон Кирхгофа является следствием из закона сохранения заряда. Заряды в узлах не могут накапливаться, т.к. изменялись бы, потенциалы узлов и токи в ветвях.
Второй закон Кирхгофа
Алгебраическая сумма Э.Д.С. в любом контуре произвольной разветвленной электрической цепи равна алгебраическом сумме падении напряжении на всех сопротивлениях контура.
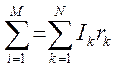 (1.10)
(1.10)
Для составления уравнения электрического равновесия цепи согласно второму закону Кирхгофа необходимо произвольно задать направление обхода контура и УПНТ. При алгебраическом суммировании Э.Д.С, падения напряжения берут со знаком "+", если направление Э.Д.С. и направление тока в элементе совпадают с направлением обхода контура, со знаком "-" - если противоположно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.