Рассмотрим
эквивалентные схемы фильтров, изображенных на рис.6.11, полагая, что
последовательные и параллельные контуры, входящие в состав фильтров имеют
одинаковые резонансные частоты. Пусть ![]() тогда эквивалентные схемы имеют вид
(рис.6.13).
тогда эквивалентные схемы имеют вид
(рис.6.13).
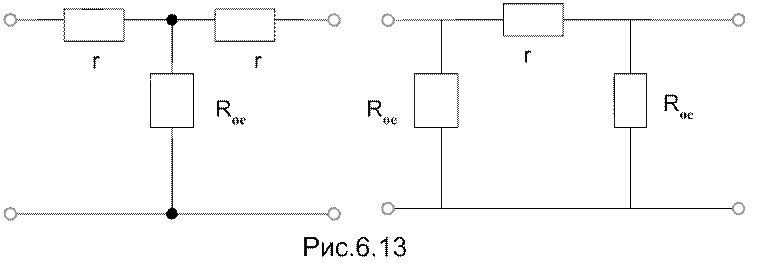
Из приведенных схем
видно, что колебания, частота которых соответствует частотам настройки
последовательных и параллельных контуров, будут проходить через фильтр от
источника в нагрузку без существенных ослабление (т.к. ![]() )
)
На частотах,
отличающихся от ![]() соотношение между
сопротивлениями, входящими в состав последовательных и параллельных плеч
существенно изменятся. Сопротивления последовательных плеч существенно
увеличится, а параллельных - уменьшатся поэтому колебания других частот, как
больших, так и меньших, чем
соотношение между
сопротивлениями, входящими в состав последовательных и параллельных плеч
существенно изменятся. Сопротивления последовательных плеч существенно
увеличится, а параллельных - уменьшатся поэтому колебания других частот, как
больших, так и меньших, чем ![]() будут
претерпевать значительное ослабление.
будут
претерпевать значительное ослабление.
Графики
частотных зависимостей ![]() и
и ![]() приведены
на рис.6.14
приведены
на рис.6.14 ![]()
|
|
|
|
|
|
|
|
|
|
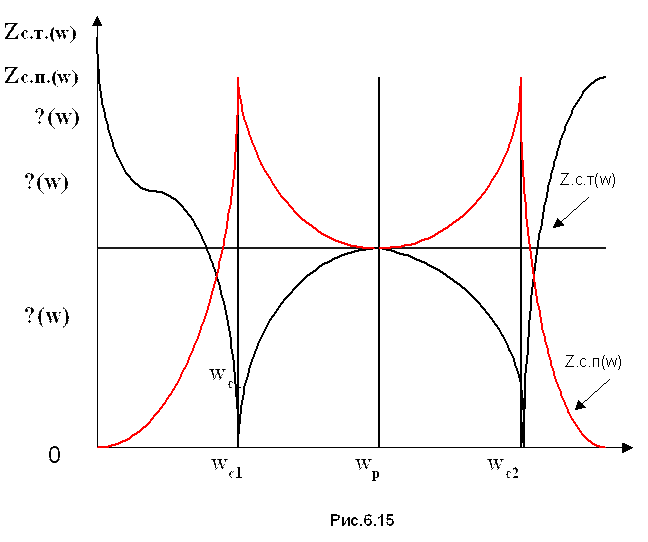
Графики частотных зависимостей и приведены на рис.6.15
|
||
|
Из приведенных графиков
видно, что полосовой фильтр обеспечивает практически беспрепятственное
пропускание колебаний в полосе частот от ![]() до
до
![]() в случае, когда фильтр работает в
согласованном режиме. Согласованный режим работы приблизительно можно
обеспечить, если сопротивление нагрузки и внутреннее сопротивление источника
выбрать равными:
в случае, когда фильтр работает в
согласованном режиме. Согласованный режим работы приблизительно можно
обеспечить, если сопротивление нагрузки и внутреннее сопротивление источника
выбрать равными:
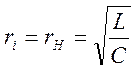
Полосовые фильтры нашли широкое применение в РЭТ.
6.7. ЗАГРАЖДАЮЩИЕ ФИЛЬТРЫ, ИХ ПАРАМЕТРЫ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
В заграждающих фильтрах /ЗФ/ последовательные плечи Т-образной .и П-образной схем содержат параллельные контуры, а параллельные плечи- последовательные контуры (рис.6.16)
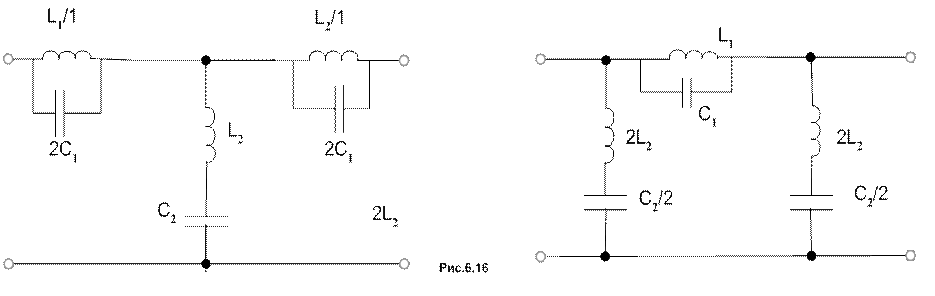
Рассмотрим эквивалентные схемы
фильтров, полагая, что в состав схем входят контуры, настроенные на одинаковую
частоту. Учитывая закон изменения сопротивлении контуров в зависимости от
частоты /рис.6.12/, на частоте ![]() получим
(рис.6.17)
получим
(рис.6.17)
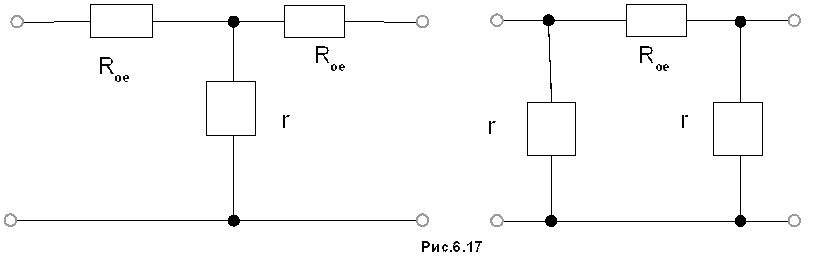
Из приведенных схем видно, что колебания, частота которых равна резонансной частоте контуров будут проходить через фильтр с большим ослаблением амплитуды.
|
|||
|
|||
|

|
|||
|
|||
|
На других частотах соотношение между сопротивлениями последовательных и параллельных плеч будет противоположным, в результате чего колебания остальных частот будут проходить на выход без ослабления.
Графики частотных зависимостей приведены на рис.6.18
![]()
Графики частотных зависимостей характеристических сопротивлений Zc.t Zсn приведены на рис.6.19
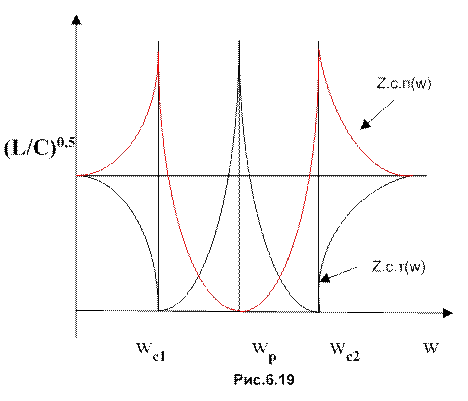
ВЫВОДЫ. Из
приведенных графиков видно, что заграждающий фильтр, работающий в согласованном
режиме, беспрепятственно пропускает от источника в нагрузку колебания
всех частот, за исключением колебаний, частота которых соответствует условию![]() колебания существенно уменьшаются
по амплитуде.
колебания существенно уменьшаются
по амплитуде.
6.8. ДРУГИЕ ТИПЫ ФИЛЬТРОВ, ПРИМЕНЯЕМЫЕ В PЭT
А. Сложные фильтры (типа_____ )
Рассмотрим ФНЧ отличающиеся тем, что часть индуктивности из последовательного плеча перенесена в параллельное (рис.6.20)
 В результате такого
переноса, как показывает анализ, выясняется, что полоса прозрачности не
изменяется. Кроме того, контур имеет резонансную частоту в полосе непрозрачности,
что позволяет получить значительно большее затухание в полосе непрозрачности, а
на частоте резонанса контура L2C2затухание будет очень большим.
В результате такого
переноса, как показывает анализ, выясняется, что полоса прозрачности не
изменяется. Кроме того, контур имеет резонансную частоту в полосе непрозрачности,
что позволяет получить значительно большее затухание в полосе непрозрачности, а
на частоте резонанса контура L2C2затухание будет очень большим.
Б. фильтры сосредоточенной селекции (ФСС)
На рис.6.21 подъедена схема ФСС, состоящего из нескольких параллельных контуров в параллельных плечах и емкостей в последовательных плечах.
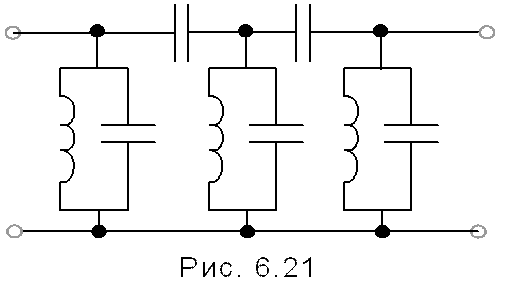

Семейство амплитудно-частотных характеристик ФСС приведено на рис.6.22
Из графика видно, что увеличивая число звеньев ФСС, можно добиться высокой избирательности.
В. RC- фильтры
В ряде случаев, с целью уменьшения габаритов фильтров вместо индуктивностей в состав фильтров включают сопротивления. Примеры таких фильтров показаны на рис.6.23

- однозвенный ФНЧ
- однозвенный ФВЧ

- полосовой фильтр
- заграждающий фильтр
6.9. РАСЧЕТ ФИЛЬТРОВ
А. Расчет ФНЧ и ФВЧ
Дано:![]()
Определить: L,C для ФНЧ

|
Дано: ![]()
Определить: L,C для ФВЧ.
|
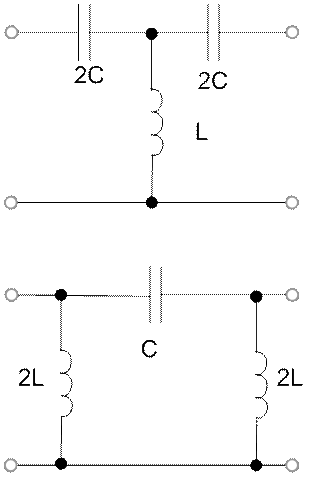
Б. Расчет ПФ
Дано:![]() граничные
частоты полосы пропускания в кГц
граничные
частоты полосы пропускания в кГц
![]()
Определить: L1 L2C1 C2 для ПФ.
|
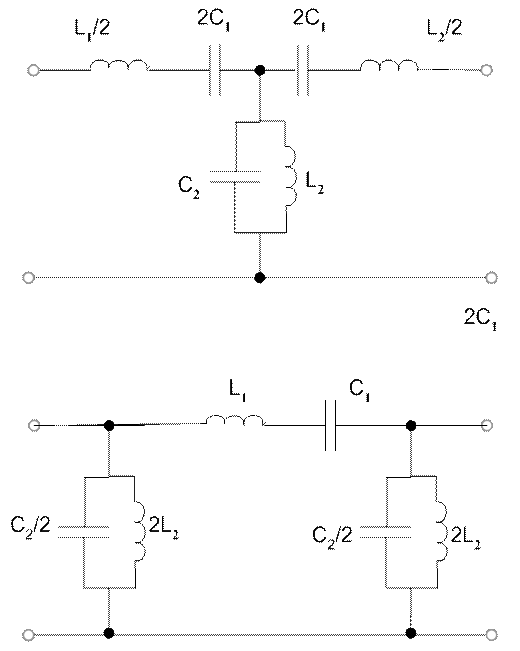
В. Расчет ЗФ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.