Для неразветвленном замкнутом цепи уравнения, составленные согласно закона Ома и второму закону Кирхгофа совпадают.
ПРИМЕР 1.4. Составить уравнение согласно второму закону Кирхгофа для цепи, изображенной на рис.1.25
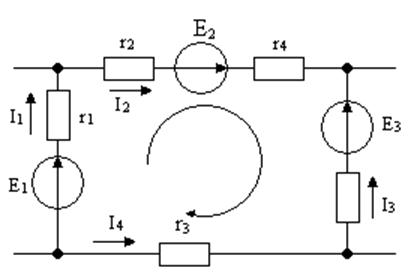 |
E1+E2-E3=I1r1+I2(r2+r4)-I3r5-I4r3
1.3.4.Эквивалентные преобразования сопротивлений
При расчете электрических цепей возникает задача определить общее (эквивалентное) сопротивление при последовательном, параллельном и смешанном соединении сопротивлении, формулы эквивалентных преобразовании выводятся на основании закона Ома.
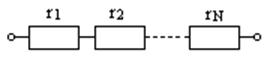
Последовательное соединение сопротивлений (рис.1.27)
 |
 |
||
![]()
Рис.1.27
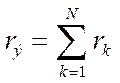 (1.11)
(1.11)
Параллельное соединение сопротивлений (рис. 1.28)
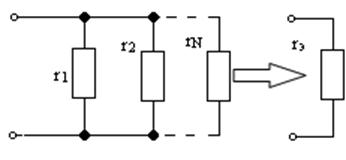 При параллельном соединении складываются проводимости
При параллельном соединении складываются проводимости
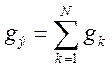
![]()
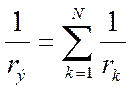
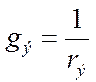
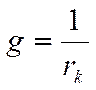
|
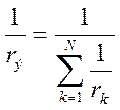 (1.13)
(1.13)
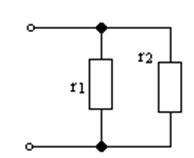
ПРИМЕР 1.5. Определить эквивалентное сопротивление цепи (рис.1.28)
 |
|||
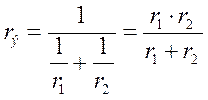 |
|||
Смешанное соединение сопротивлений
При смешанном соединении преобразование сводится к поочередному преобразованию последовательно и параллельно соединенных сопротивлении.
ПРИМЕР 1.6. Определить эквивалентное сопротивление цепи (рис.1.29)
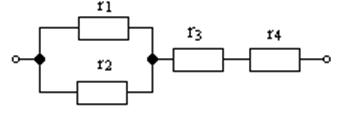 |
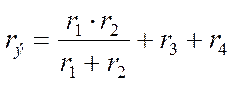
Рис.1.29
Преобразование "треугольника” в "звезду" и "звезды" в "треугольник"
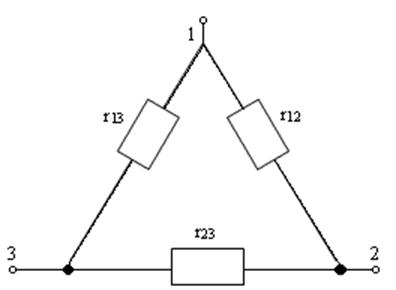 |
|||
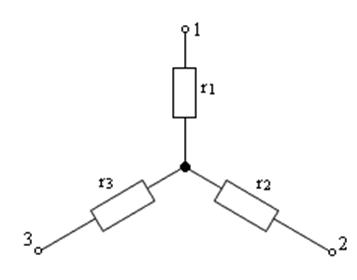 |
|||
Рис.1.30а Рис.1.30б
Считая известными "стороны треугольника", можно рассчитать “лучи звезды”:
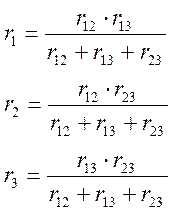 а)
а)
(1.14)
(1.15)
(1.16)
и наоборот, считая известными "лучи звезды", можно рассчитать "стороны треугольника":
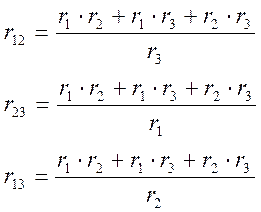 б) (1.17)
б) (1.17)
(1.18)
(1.19)
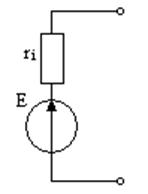
Преобразование схем с источниками Э.Д.С. и тока
 |
 |
||
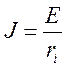
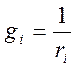 а)
(1.20)
а)
(1.20)
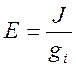
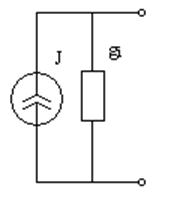
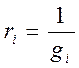 б)
(1.21)
б)
(1.21)
Рис.1.32
Применение метода эквивалентных преобразования будем рассматривать совместно с последующим материалом.
1.4.ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ СИНУСОИДАЛЬНОГО ТОКА
1.4.1. Синусоидальный ток и его основные параметры
Ток (э.д.с., напряжение), значение которого во времени изменяется, называется переменным. В электрорадиотехнике наибольшее практическое значение имеют периодические токи (э.д.с, напряжения), являющиеся синусоидальными функциями времени.
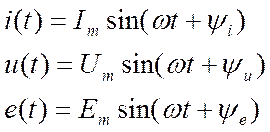 (1.22)
(1.22)
 Величины
i(t), u(t), e(t) называют
мгновенными значениями, а форма представления (1.22) – аналитической.
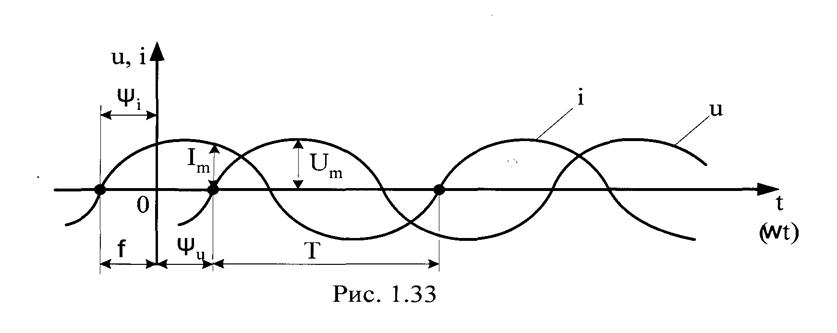
График такой величины (рис.1.ЗЗ) – называется развернутой диаграммой.
Величины
i(t), u(t), e(t) называют
мгновенными значениями, а форма представления (1.22) – аналитической.
График такой величины (рис.1.ЗЗ) – называется развернутой диаграммой.
Основными параметрами синусоидальных величин являются:
1) Амплитуда Im, Um, Em – максимальное значение синусоидальной величины (рис.1.33);
2) Период Т – наименьший интервал времени, по истечении которого значение тока (э.д.с., напряжения) повторяются;
Частота f, F– величина, обратная периоду
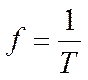 |
(1.23)
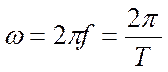 |
Угловая частота ω - (1.24)
3) Момент времени, в который синусоидальная величина равна нулю и переходит от отрицательного значения к положительному, называется началом периода.
Аргумент синуса, отсчитываемый от начала периода называется фазой. Аргумент синуса, отсчитываемый от начала периода до t=0, называется начальной фазой. (Рис.3.33 – ψi, yu)
Положительные начальные фазы откладывают влево от начала координат, отрицательные – вправо.
Алгебраическая величина, равная разности начальных фаз синусоидальных величин называется сдвигом фаз – f= yu-ψi.
Таким, образом, синусоидальная величина может быть однозначно задана тремя параметрами:
1) амплитудой,
2) частотой,
3) начальной фазой.
При известной частоте – двумя параметрами:
1) амплитудой,
2) начальной фазой.
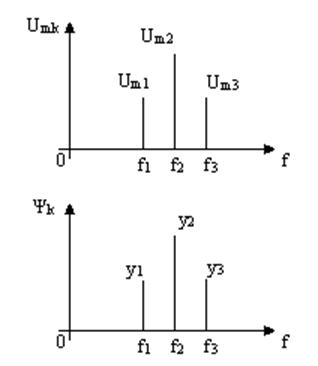 Любую синусоидальную величину можно представить в виде
двух связанных графиков: (рис.1.34) Совокупность таких графиков называется
спектральной диаграммой или спектром.
Любую синусоидальную величину можно представить в виде
двух связанных графиков: (рис.1.34) Совокупность таких графиков называется
спектральной диаграммой или спектром.
Рис.1.34
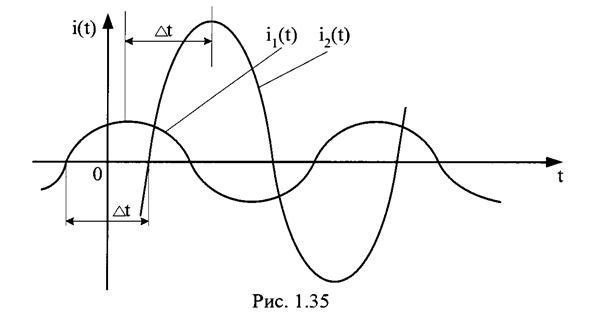
Если имеется несколько синусоидальных величин, изменяющихся с одинаковой "частотой, начальные фазы которых неодинаковы, то говорят, что они сдвинуты одна относительно другой по фазе (рис.1.35).
 ПРИМЕР
1.7. Величина i1(t) опережает
ПРИМЕР
1.7. Величина i1(t) опережает
i2(t) на величину φ=ω·Δt (рис.1.35)
Кроме рассмотренных выше параметров синусоидальный ток характеризуют еще средним и действующим значениями.
Действующим значением синусоидального тока называют его среднее квадратическое значение за период:
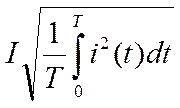 |
(1.25)
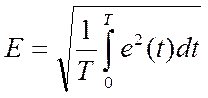
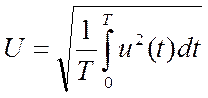 Аналогично, действующими значениями напряжения и
э.д.с. называют величины:
Аналогично, действующими значениями напряжения и
э.д.с. называют величины:
Определим действующее значение синусоидального тока:
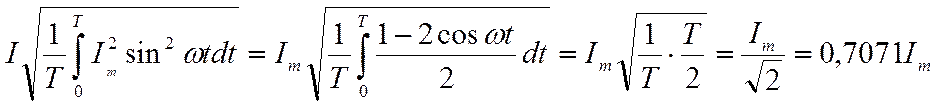 |
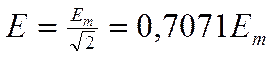
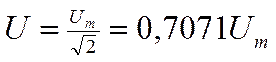 Аналогично:
Аналогично:
Средним значением синусоидального тока называют среднее значение за половину периода, определяемое выражением
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.