Электротехника \ Радиотехнические цепи и сигналы

Линейные цепи в установившемся режиме: Курс лекций, страница 27

В том случае, когда контуры полностью идентичны, т.е. не только L1=L2,  C1=C2,  но и r1=r2,  тогда 

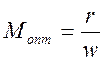
оптимальное сопротивление связи равно         xсв.опт=wMопт=r       и опти­мальный коэухрквдент  связи между контурами равен

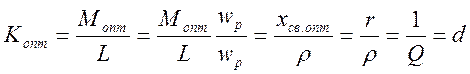                                      (4.60)

ВОПРОСЫ:

1.  Что называется резонансом в системе связанных колебательных контуров?

2.  Что такое первый частные резонанс?

3.  Сформулируйте условие первого частного резонанса?

4.  Что такое второй частный резонанс?

5.  Что такое полный резонанс?

4.4.5. Частотные характеристики и полоса пропускания системы индуктивно-связанных контуров

Избирательные свойства системы индуктивно связанных контуров   оределяются ее комплексной передаточной функцией по напряжению

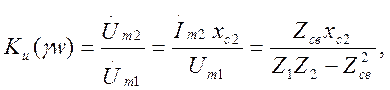                                                            (4,61)

т.к. 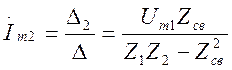                                                                                   (4.62)

Далее будем рассматривать систему из идентичных контуров с высокой добротностью. В этом случае все интересующие нас изменения частотных характеристик будут сосредоточены в узком диапазоне частот, при этом будем считать,

что  ω=ω0 В этом случае выражение АЧХ системы будет равно

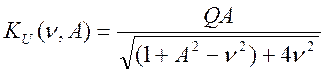                                              (4.63)

 где                              

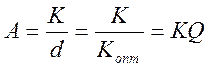
                                                        -фактор связи или нормированные (к своему оптимальному значению) коэффициент связи между контурами,

                                       

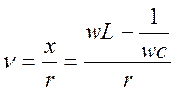
          - обобщенная расстройка.

Вначале рассмотрим как зависит данная функция от величины фак-тора связи на резонансной частоте.

В этом случае

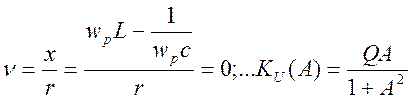                                  (4.46)

График данной функции приведён на рис. 4.40:

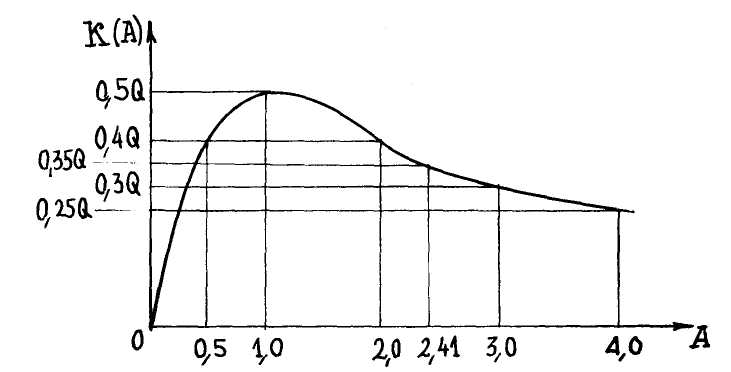
Из приведенного рисунка видно,  что при полном резонансе, т.е.

когда оба контура настроены на рабочую частоту    /υ=0/ и при

оптимальной связи 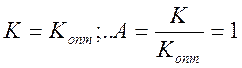   ,  имеет место максимальное значение АЧХ  системы.

Целесообразно рассмотреть поведение пункции 4.63 при некоторых фиксированных значениях величины фактора связи А. Имеет смысл рассмотреть следующие три случая:

-  АЧХ системы при слабом связи между контурами,  когда А < 1;

-  АЧХ системы при оптимальной связи между контурами, когда А=1 ;

-  АЧХ системы при сильной связи между контурами, когда А >1.

АЧХ системы связанных контуров при слабой связи

Пусть фактор связи   А0,3. Рассмотрим аналитическое выраже­ние АЧХ для данного случая.

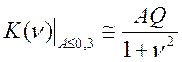                                                      (4.65)

Определим полосу пропускания системы связанных контуров при сла­бой связи. Значения АЧХ на граничных частотах должны быть в  раз меньше максимального значения АЧХ,  которое при нулевой расстройке равно   K(0)=AQ.

 Значения АЧХ на граничных частотах должны быть равны   ( в  раз или в 1.41 раза меньше)

,

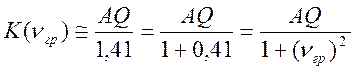отсюда

Сравним граничные значения обобщенной расстройки, полученные для системы контуров с граничными значениями обобщённой, расстройки для одиночного контура (например,  последовательного):

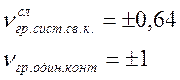
Из приведенных выражений видно, что полоса пропускания системы идентичных контуров при слабой связи ( А  0,3 ) составляет при­мерно 64 % ширины полосы пропускания каждого из контуров входящих в систему. Таким образом, для слабой связи можно считать, что по­лоса пропускания системы контуров равна:


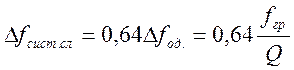                                                (4.66)

а граничные частоты полосы пропускания равны

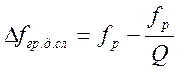                           и 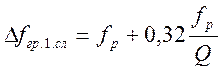                                     (4.67)

Семейство АЧХ системы при слабой. связи приведено на рис.4.41. Приближенно можно считать,  что полоса пропускания системы во всех трех случаях /А-0;1 ; А-0,2; А=0,3/ одинакова.

                            

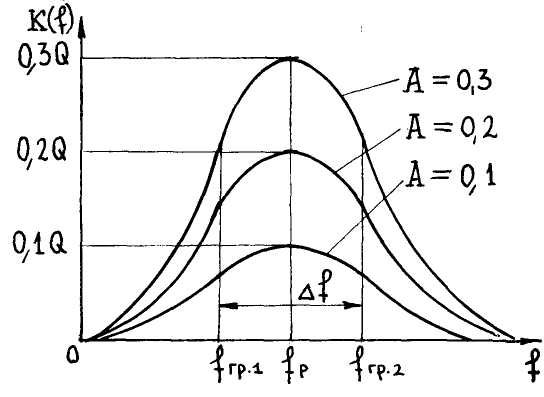
Рис. 4.41

АЧХ системы связанных контуров при оптимальной связи

Пусть фактор связи А=1,  тогда аналитические выражения AЧХ для данного случая будут:

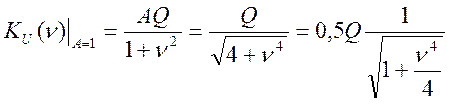                                   (4.68)

Определим полосу пропускания системы связанных контуров при оптимальной связи. Значение АЧХ на резонансной частоте (при υ=0) равно: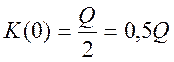                          

Значения АЧХ на граничных частотах должны быть равны (в  раз или 1,41 раза меньше):

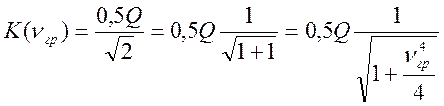
отсюда                         


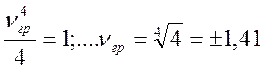
Сравним граничные значения обобщенной расстройки, полученные для системы с оптимальной связью,  с граничными значениями обобщен­ной расстройки одиночного контура: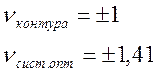

Из приведенных выражений видно, что полоса пропускания системы идентичных контуров при оптимальной связи составляет примерно 141% ширины полосы пропускания каждого из контуров, входящих в систему.

Таким образом, для оптимальной связи можно считать, что полоса пропускания системы равна:

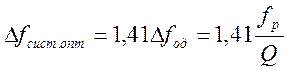                                                (4.69)

а граничные частоты полосы пропускания равны


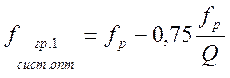
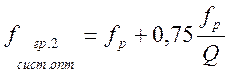                                     (4.70)

Рис. 4.42

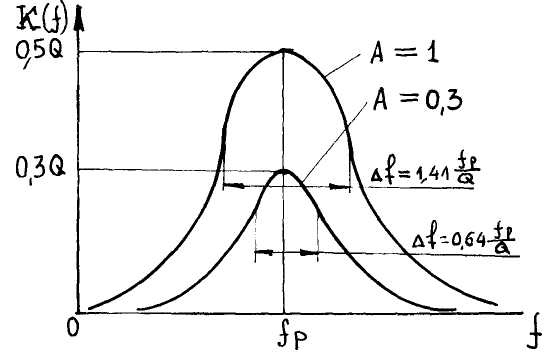
На рис.4.42 приведена АЧХ системы при оптимальной связи   (А=1) в сравнении, с АЧ1 системы при слабой свя­зи    (А=0,3).

АЧХ системы связанных контуров при сильной связи

Для связи между контурами больше оптимальной, аналитическое выражение АЧХ соответствует выражению(4.63). В отличие от двух рассмотренных случаев, график АЧХ при сильной связи являемся дву­горбым (рис.4.43).


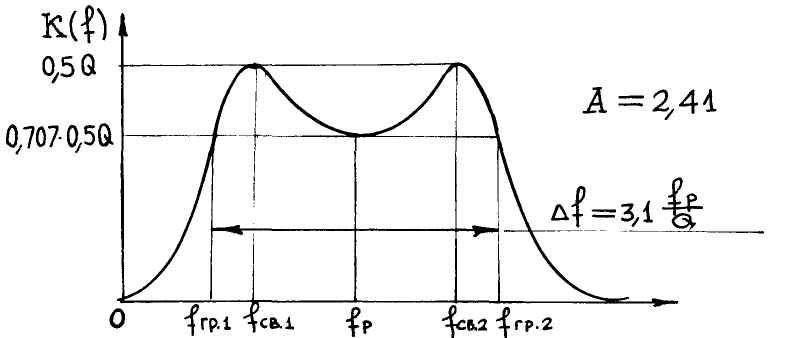
Рис. 4.43

На приведенном рисунке изображен график АЧХ при  А=2,41. При таком значении фактора связи обеспечивается максимально воз­можная ширина полосы пропускания системы контуров:

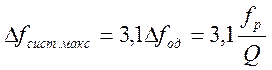                                         (4.71)

граничные частоты полосы пропускания равны:

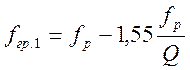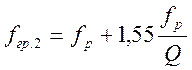;                                (4.72)

Скачать файл