РЕШЕНИЕ.:
1. Значение коэффициента усиления на резонансной частоте вычислено при решении, предыдущего примера и равно:
![]()
2. Значение коэффициента усиления на произвольной частоте равно:
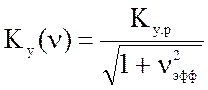 , где
, где 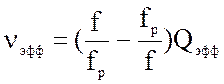
а) для
![]() будем иметь
будем иметь 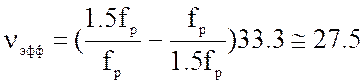
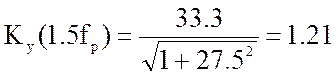
б) для
![]() будем иметь
будем иметь 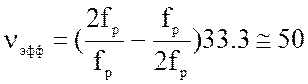
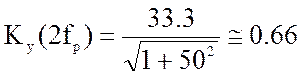
Выводы.
1.
Параллельный контур, как и последовательный, обладает частотно
-
избирательными свойствами.
2. В отличие от последовательных контуров, параллельные контуры не обладают "усилительным" действием, поэтому их применяют в составе усилителей, которые компенсируют ослабление сигналов.
4.4. СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
В современной радиотехнической аппаратуре широко применяются не только одиночные, но и связанные колебательные контуры, это обусловлено тем, что избирательность одиночных контуров во многих случаях является недостаточной. Анализируя выражения 4.9, 4.10, выведенные для последовательного контура, и 4.25 для параллельного контура, можно видеть, что амплитудно-частотные характеристики одиночных контуров описываются выражением:
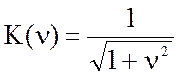 ,
(4.31)
,
(4.31)
где ![]() - обобщенная расстройка.
- обобщенная расстройка.
Сравнивая значения АЧХ для частот, лежащих в полосе пропускания (![]() ) и для частот вне полосы пропускания
(
) и для частот вне полосы пропускания
(![]() ), следует отметить, что даже при (
), следует отметить, что даже при (![]() ), что соответствует расстройке на величину,
равную пяти полосам пропускания, значение АЧХ соответствует 0,1 от своего
максимального значения (см.таблицу), что явно недостаточно для качественной селекции сигналов.
), что соответствует расстройке на величину,
равную пяти полосам пропускания, значение АЧХ соответствует 0,1 от своего
максимального значения (см.таблицу), что явно недостаточно для качественной селекции сигналов.
|
|
0 |
1 |
2 |
5 |
10 |
100 |
|
|
1 |
0,707 |
0,45 |
0,197 |
0,1 |
0,01 |
В связи с тем, что одиночные контуры не обеспечивают высокую селективность, имеющую значительно более высокую избирательность, а также обладающие возможностью регулировки полосы пропускания в широких пределах.
4.4.1. Виды связи между контурами
Связь между отдельными контурами системы осуществляется при помощи элементов связи. Элементами связи могут быть: индуктивность, емкость, сопротивление, взаимоиндуктивность и их комбинации. На рисунки 4.31 приведен ряд схем, иллюстрирующих это положение.
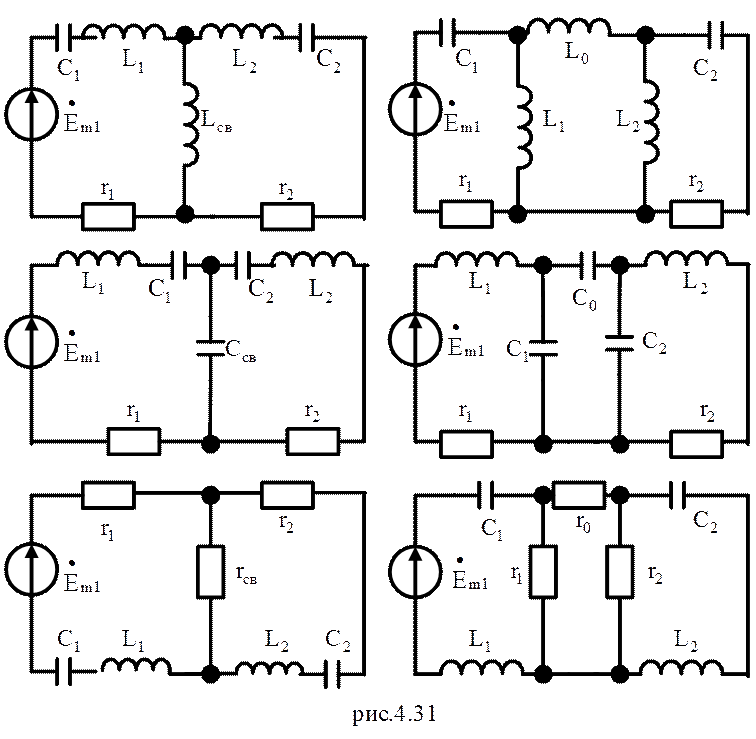
Следует отметить, что в левом столбце на рисунки 4.31 приведены схемы с Т-образной схемой связи, а в правом столбце - с П-образной схемой связи. Кроме того, в первой строке помещены схемы с индуктивной, во второй - с емкостной, и в третьей - с гальванической связью. Часто схемы с Т-образной схемой связи называют схемами с внутренней связью, а схемы с П-образной схемой связи схемами с внешней связью. Такое название эти схемы получили в связи с тем, что в схемах с внутреннем связью элементы связи входят в состав обоих контуров, а в схемах с внешней связью -не входят в состав контуров.
Широкое распространение получили схемы со взаимной индуктивностью (рис.4.32 и 4.33).
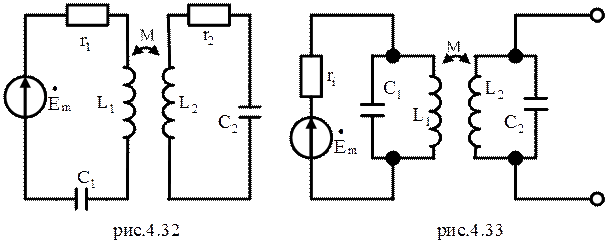
Схема, приведенная на рисунки 4.32, применяется в тех случаях, когда внутреннее сопротивление источника не велико, такая система состоит из 2-х индуктивно-связанных последовательных колебательных контуров. Схема, приведенная на рис.4.33, применяется в тех случаях, когда внутреннее сопротивление источника велико, такая система состоит из 2-х индуктивно-связанных колебательных контуров, причем первичный контур является параллельным, а вторичный контур - последовательным.
4.4.2. Сопротивление связи и коэффициент связи
Связь между контурами характеризуют сопротивлением связи. Сопротивлением связи называют сопротивление, общее для обоих контуров. Эту величину легко найти для Т-образной схемы связи, а для П-образной схемы при слабой связи можно считать, что Zcв=Zo, где Zo - комплексное сопротивление последовательной ветви. Эти величины для схем, приведенных на рис.4.31 соответствуют:
для левого столбца схем: для правого столбца схем при
слабой связи:
![]()
![]()
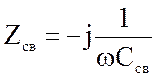
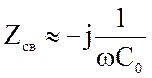 (4.32)
(4.32)
![]()
![]()
для схем со взаимно-индуктивной трансформаторной связью сопротивление связи равно:
![]() (4.33)
(4.33)
Степень влияния связанных контуров друг на друга оценивается коэффициентом связи, для его определения выделяют участок схемы, образованный элементом связи и элементами контуров, одноименными с элементом связи. Такой участок цепи имеет четыре зажима и называется четырехполюсником связи.
Коэффициентом связи называется среднее геометрическое
значение
модулей коэффициентов передачи по напряжению четырехполюсника связи в
прямом и обратном направлениях: ![]() (4.34)
(4.34)
для индуктивное связи получаем:
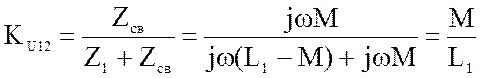 (4.35)
(4.35)
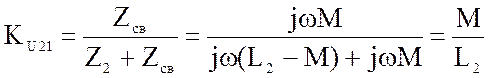 (4.36)
(4.36)
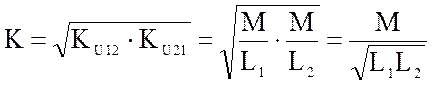 (4.37)
(4.37)
Коэффициент
связи не может быть больше единицы. Его значения находятся в
пределах: ![]() .
.
В общем случае при реактивном сопротивлении связи для коэффициента связи можно записать:
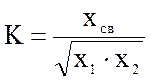 (4.38)
(4.38)
где x1 и x2 - реактивные
сопротивления элементов первого и второго контуров, одноименных с элементами
связи. Так как в радиотехнике наибольший интерес представляет режим резонанса,
когда индуктивное и емкостное сопротивления элементов контуров (![]() ) выражение /
) выражение /
(4.36) можно записать:
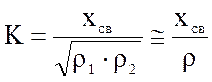 (4.39)
(4.39)
4.4.3. Вносимые сопротивления эквивалентные схемы системы двух индуктивно-связанных контуров
Используя
схему замещения трансформатора, преобразуем схему с трансформаторной
связью в схему с внутренней (Т-образной)
связью
(рис.4.34).
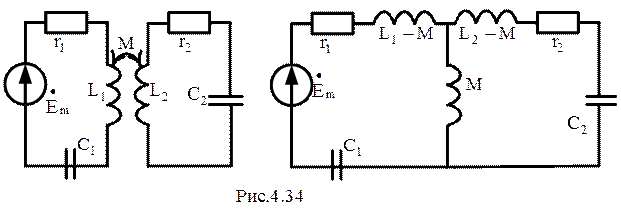
Найдем токи в контурах методом контурных токов. Рассчитаем собственные и взаимные сопротивления контуров, а также контурные э.д.с.:
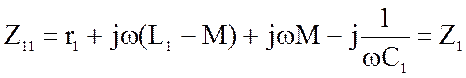 (4.40)
(4.40)
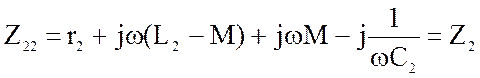 (4.41)
(4.41)
![]() (4.42)
(4.42)
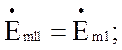
![]() (4.43)
(4.43)
Составим систему уравнений:
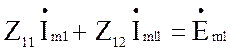
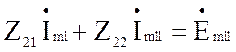 (4.44)
(4.44)
Подставляя в систему уравнений значения собственных и взаимных сопротивлений и контурные э.д.с, получим:
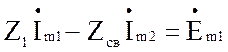
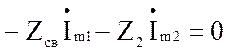 (4.45)
(4.45)
Решая систему уравнений относительно неизвестных токов, получим:
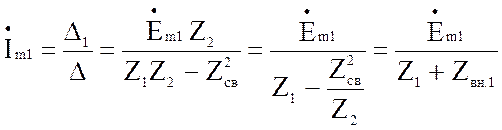 (4.46)
(4.46)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.