ПРИМЕР4.1. Определить значения АЧХ. и ФЧХ последовательного контура с параметрами L = 100мкГн, C= 100пФ, r= 10 Ом на частоте 2МГц,
РЕШЕНИЕ:
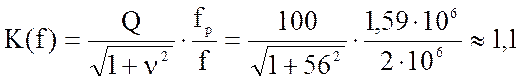 ;
;
![]() ;
;
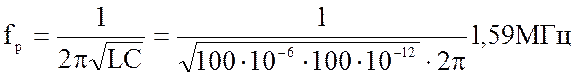 ;
;
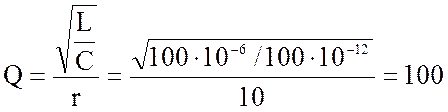 ;
;
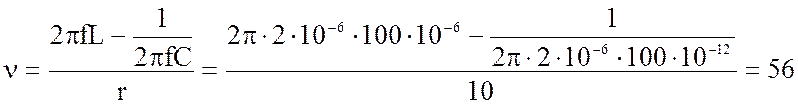 ;
;
4.2.5. Анализ влияния первичных параметров на амплитудно-частотные характеристики контура
На приведенных рисунках (рис.4.10-4.12) приведены графики амплитудно-частотных характеристик контура, отражающие влияние, изменения первичных параметров.

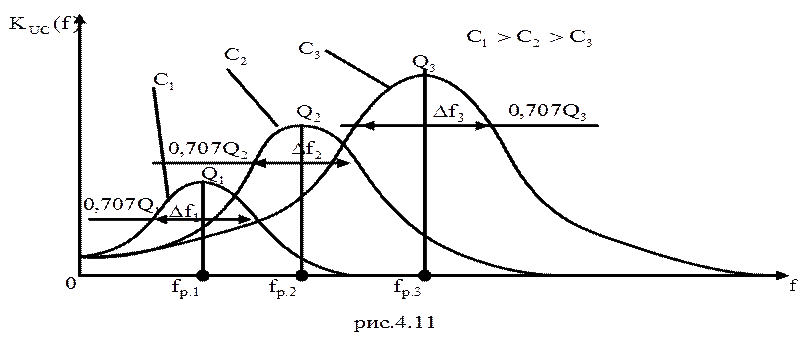

Анализируя графики АЧХ изображенные на рисунки 4.11. можно сделать вывод о том, что изменение емкости контура приводит к соответствующим изменениям резонансной частоты, однако полоса пропускания контура при этом не изменяется.
4.2.6. Зависимость модуля контурного сопротивления от частоты
Комплексное сопротивление последовательного контура равно:
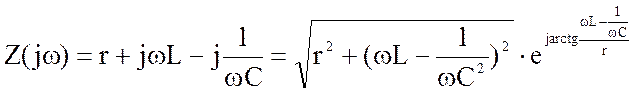 (4.15)
(4.15)
или ![]()
Изобразим на рисунки 4.13 графики зависимостей сопротивлений элементов контура и модуля комплексного сопротивления контура от частоты.
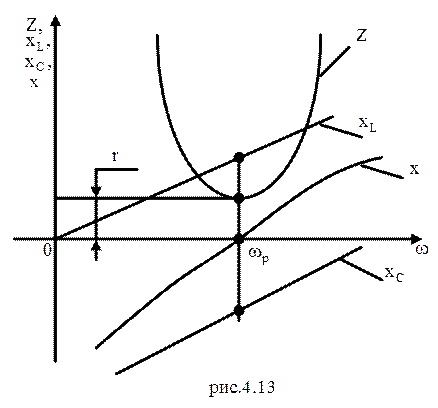
Вывод: Последовательный колебательный контур обладает большим сопротивлением в широком диапазоне частот, за исключением небольшой области частот вблизи резонансной частоты.
4.2.6. Применение последовательных колебательных контуров
Последовательные колебательные контуры широко применяются в радиотехнике.
 На рисунки 4.14 в
качестве примера приведена схема входной цепи радиоприемника. В такой схеме через
катушку будут протекать токи высокой частоты с различными частотами за счет
приема антенной излучений передающих радио станций. Эти токи наводят в катушке L2 совокупность э.д.с
различных частот. Изменением емкости С настраивают колебательный контур на требуемую
частоту. При этом в контуре возникает явление резонанса на данной частоте. Напряжение
на емкости С при этом будет в Q. раз больше, чем э.д.с. данной частоты, наводимая в катушке
L2. На других частотах
явление резонанса отсутствует, поэтому напряжение на емкости контура за счет
других станций будет во много раз меньше. Таким образом, входная цепь
радиоприемника выполняет функции селекции (выделения) и "усиления"
колебаний.
На рисунки 4.14 в
качестве примера приведена схема входной цепи радиоприемника. В такой схеме через
катушку будут протекать токи высокой частоты с различными частотами за счет
приема антенной излучений передающих радио станций. Эти токи наводят в катушке L2 совокупность э.д.с
различных частот. Изменением емкости С настраивают колебательный контур на требуемую
частоту. При этом в контуре возникает явление резонанса на данной частоте. Напряжение
на емкости С при этом будет в Q. раз больше, чем э.д.с. данной частоты, наводимая в катушке
L2. На других частотах
явление резонанса отсутствует, поэтому напряжение на емкости контура за счет
других станций будет во много раз меньше. Таким образом, входная цепь
радиоприемника выполняет функции селекции (выделения) и "усиления"
колебаний.
ПРИМЕР 4.2. Для последовательного колебательного контура на входе усилителя высокой частоты рассчитать и построить график АЧХ
 входной цепи по 5 точкам:
для частот
входной цепи по 5 точкам:
для частот ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() , если С =100пФ L= 100мкГн, r =10 Ом, где r- сопротивление проводов
контура.
, если С =100пФ L= 100мкГн, r =10 Ом, где r- сопротивление проводов
контура.
РЕШЕНИЕ:
1. Вычисление вторичных параметров:
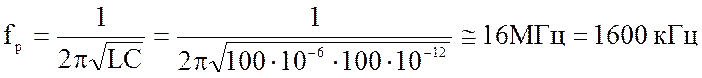
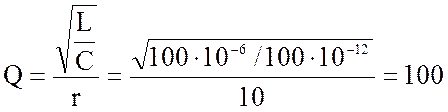
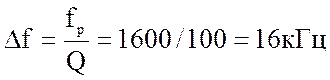
2. Вычисление граничных частот:
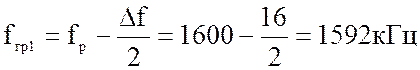
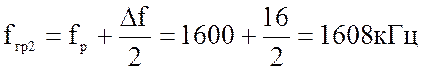
3. Определение значений АЧХ на указанных частотах:
|
|
|
|
|
|
|
|
|
1 |
0.707Q |
Q=100 |
0.707=70.7 |
0 |
Значение АЧХ равно нулю, т.к. отсутствует гальваническая связь между катушками.
4. Построение графика АЧХ осуществляют путем построения примерного графика по 5 точкам, приведенным в таблице.
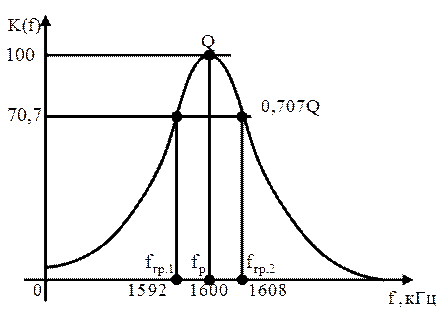
ПРИМЕР 4.3. Для схемы, приведенной в предыдущей задаче известно, что в катушке контура за счет взаимной индукции из антенной цепи наводится полезный сигнал:
![]()
и помеха
![]()
Известно, что fc = fp , а fп = 2fp
Определить отношение сигнал/помеха на входе и на выходе, во сколько раз улучшилось отношение сигнал/помеха.
1. Определить отношение сигнал/помеха на входе контура:
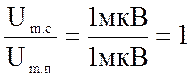
2. Определить значения АЧХ контура на частотах:
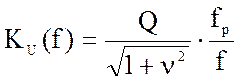
где 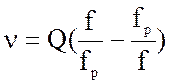
для ![]()
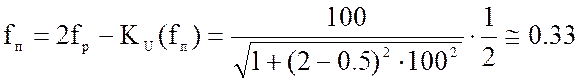
3. Определить амплитуды сигнала и помехи на выходе контура:
Амплитуда сигнала:
![]()
Амплитуда помехи:
![]()
4.Отношение сигнал/помеха на выходе контура равно:
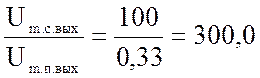
Из
расчетов можно сделать вывод, что контур обладает избирательными свойствами. Он
"усиливает" сигнал на своей резонансной частоте( Um.c. увеличивается
в 100раз) и подавляет помеховый сигнал на частоте ![]()
(Um.п. уменьшается в 3 раза).
4.3. ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
4.3.1.Условие и признаки резонанса токов
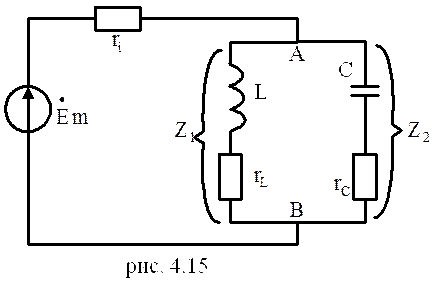 Резонансом токов называют явление при
котором токи через реактивные элементы L и С значительно
превышают ток, потребляемый контуром от источника. Резонанс токов наступает,
когда сопротивление участка цепи. АВ (рис.4.15) является чисто активным.
Резонансом токов называют явление при
котором токи через реактивные элементы L и С значительно
превышают ток, потребляемый контуром от источника. Резонанс токов наступает,
когда сопротивление участка цепи. АВ (рис.4.15) является чисто активным.
Рассмотрим комплексное сопротивление участка цепи АВ:
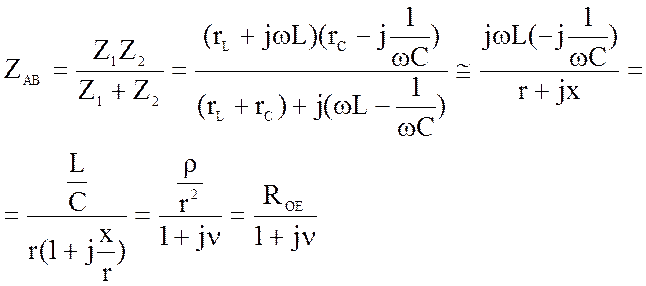 (4.16)
(4.16)
Эта величина является чисто активной в случае, если X= Хс, при этом резонансная частота равна
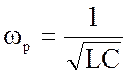 или
или 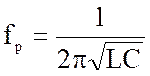 (4.17)
(4.17)
Таким образом, условием резонанса токов является равенство нулю реактивного сопротивления
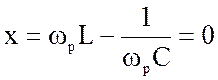 ;
; 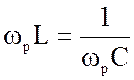 (4.18)
(4.18)
На резонансной частоте сопротивление параллельного контура чисто активное и максимальное
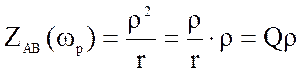 (4.19)
(4.19)
На остальных частотах модуль комплексного сопротивления контура меньше, график зависимости приведен на (рис4.16).
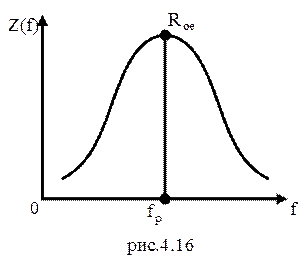
Признаками резонанса токов являются:
1. Ток в общей цепи минимальный и совпадает с э.д.с. по фазе:
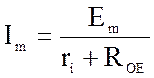 (4.20)
(4.20)
2.Токи в ветвях контура равны по величине, противоположны по фазе и в Q paз превышают ток в неразветвленной (общей) части цепи.
Полагая ![]() ,
имеем
,
имеем
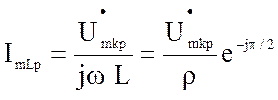 (4.21)
(4.21)
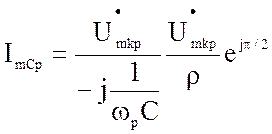 (4.22)
(4.22)
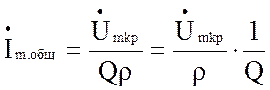 (4.23)
(4.23)
ВОПРОСЫ:
1. Что называют резонансом токов?
2. Сформулируйте условие резонанса токов?
3. Какие существуют признаки резонанса токов?
4.3.2. Основные параметры системы «генератор-параллельный контур-нагрузка»
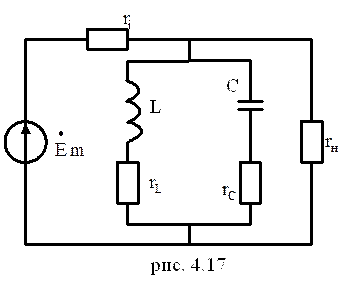 Как правило, параллельный колебательный
контур используется в системе, приведенной на рисунки 4.17. Рассмотрим основные
параметры системы. К первичным параметрам системы
следует отнести первичные параметры r, L, С, значения
внутреннего сопротивления источника и нагрузки riи rн.
Как правило, параллельный колебательный
контур используется в системе, приведенной на рисунки 4.17. Рассмотрим основные
параметры системы. К первичным параметрам системы
следует отнести первичные параметры r, L, С, значения
внутреннего сопротивления источника и нагрузки riи rн.
Вторичные параметры системы таковы:
1.  или
или 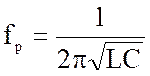 -
резонансная частота
-
резонансная частота
2. 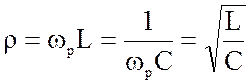 - волновое или характеристическое
сопротивление
- волновое или характеристическое
сопротивление
3. 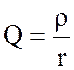 - добротность нешунтированного
контура.
- добротность нешунтированного
контура.
4. 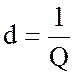 - затухание нешунтированного контура
- затухание нешунтированного контура
5. 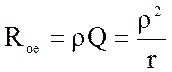 - сопротивление контура на
резонансной частоте
- сопротивление контура на
резонансной частоте
6. 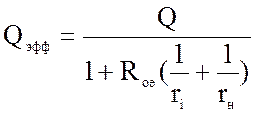 - эффективная добротность системы
«генеретор- контур-нагрузка»
- эффективная добротность системы
«генеретор- контур-нагрузка»
7. 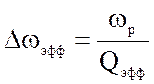 или
или 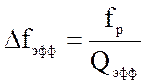 -
полоса пропускания системы «генератор-контур-нагрузка»
-
полоса пропускания системы «генератор-контур-нагрузка»
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.