|
ВЫВОДЫ:
1.
В цепи с индуктивностью напряжение
опережает ток на ![]() .Þ сдвиг по фазе на
.Þ сдвиг по фазе на ![]() .
.
2. Мощность изменяется по синусоидальному закону с двойной частотой. При положительном значении электрическая энергия запасается в магнитном поле катушки. В момент времени, когда она отрицательна, передается источнику электрической энергии.
ЦЕПЬ СИНУСОИДАЛЬНОГО ТОКА С ЕМКОСТЬЮ.
![]() Если к емкости С (рис. 1.48) приложить синусоидальное
напряжение то в цепи потечет ток
Если к емкости С (рис. 1.48) приложить синусоидальное
напряжение то в цепи потечет ток
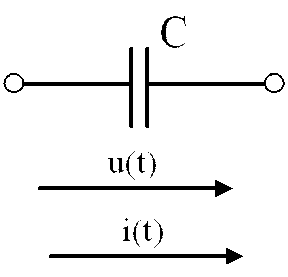
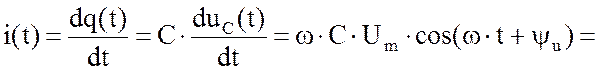
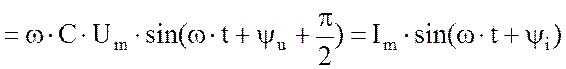
|
![]() где - амплитуда
тока,
где - амплитуда
тока,
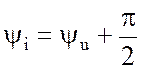
- начальная фаза.
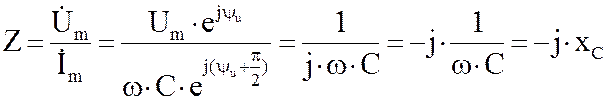 |
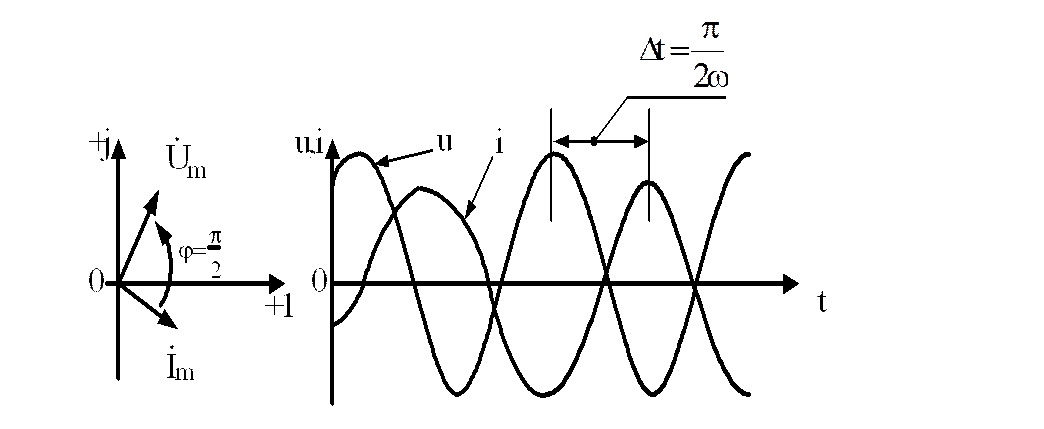

|
ВЫВОДЫ:
1.
Ток, протекающий через емкость,
опережает напряжение на ![]()
2. Мощность является знакопеременной, изменяется с двойной частотой. При положительном значении электрическая энергия накапливается в магнитном поле емкости. В момент времени, когда она отрицательна, передается из емкости в источник электрической энергии.
3. Комплексное сопротивление активного сопротивления является вещественной величиной и от частоты не зависит.
4. Комплексное сопротивление индуктивности является мнимой величиной и прямо пропорционально частоте.
5. Комплексное сопротивление емкости является отрицательной величиной и обратно пропорционально частоте.
6. Сопротивления индуктивности и емкости называют реактивными сопротивлениями.
1.6. ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
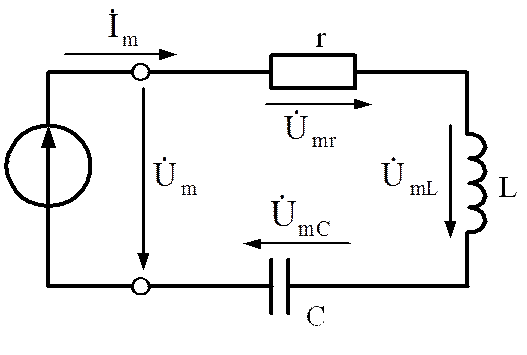
1.6.1. Цепь синусоидального тока с последовательным соединением элементов r, L и С.
то по ней потечет синусоидальный ток .
Так как напряжение на активном сопротивлений совпадает по
фазе с током, на индуктивности опережает по фазе ток на ![]() , а на емкости отстает по фазе от
тока на
, а на емкости отстает по фазе от
тока на ![]() , то на основании второго закона
Кирхгофа для мгновенных значении можно записать:
, то на основании второго закона
Кирхгофа для мгновенных значении можно записать:
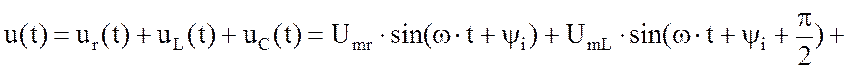
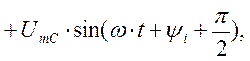 |
|||||
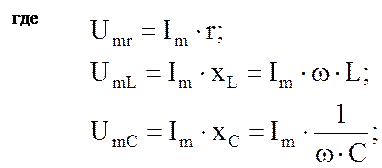 |
|||||
|
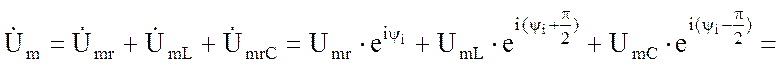 |
|||
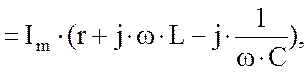 |
|||
(1.43)
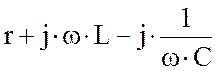 |
- комплексное сопротивление цепи |
где
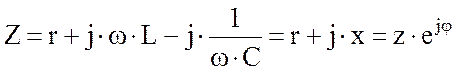 |
- реактивное сопротивление цепи, - аргумент полного сопротивления цепи, - модуль полного сопротивления цепи. |
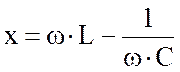 |
||||||
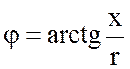 |
||||||
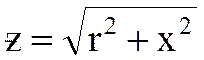 |
||||||
Характер комплексного сопротивления цепи зависит от соотношения между ХL и ХС.
![]() 1. Если
ХL> XС, то при этой ток будет отставать по фазе от
приложенного напряжения, цепь носит активно-индуктивный характер (Рис.1.52а).
1. Если
ХL> XС, то при этой ток будет отставать по фазе от
приложенного напряжения, цепь носит активно-индуктивный характер (Рис.1.52а).
![]() 2. Если
ХL<ХС, то при
этом ток будет опережать по фазе приложенное
2. Если
ХL<ХС, то при
этом ток будет опережать по фазе приложенное
напряжение. Цепь носит активно-емкостный характер (Рис.1.52 б).
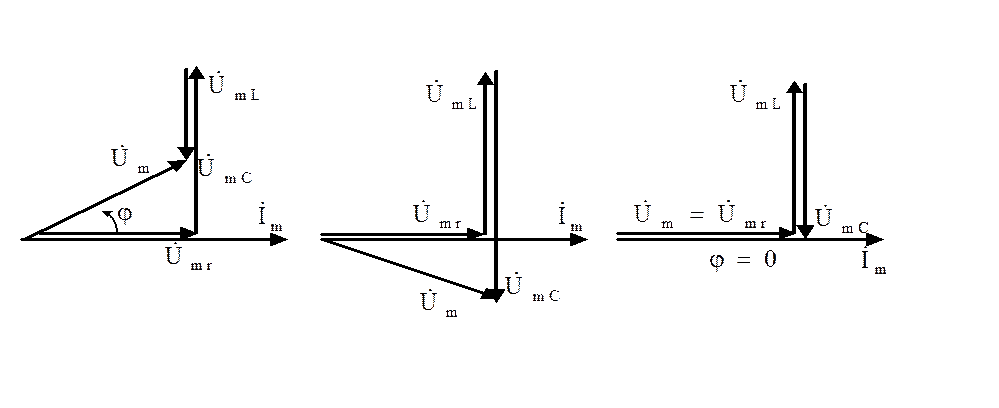
![]() 3. При Х=ХС сдвиг фаз при этом ток
в цепи совпадает по фазе с приложенным напряжением, цепь носит характер чисто
активного сопротивления (Рис. 1.52 в).
3. При Х=ХС сдвиг фаз при этом ток
в цепи совпадает по фазе с приложенным напряжением, цепь носит характер чисто
активного сопротивления (Рис. 1.52 в).
а) б) в)
Рис. 1.52
Рассматриваемое явление в пени синусоидального тока с последовательным соединением r, L, С, при котором ток в цепи и приложенное к ней напряжение совпадают по фазе, а сопротивление является чисто активным, называют резонансом напряжений. При таком резонансе напряжения на реактивных элементах L и С могут во много раз превышать приложенное к контуру напряжение. Отсюда название "резонанс напряжений".
![]()
![]() Следует ответить, что при изменении частоты реактивные
сопротивления ХLи ХС будут изменяться, т.к. они являются
функциями частоты. При этом полное сопротивление цепи и ее характер также будет
изменяться. На одних частотах цепь будет носить активно-индуктивный характер,
на других активно-емкостный, а на некоторой частоте - называемой резонансной
частотой - чисто активный характер.
Следует ответить, что при изменении частоты реактивные
сопротивления ХLи ХС будут изменяться, т.к. они являются
функциями частоты. При этом полное сопротивление цепи и ее характер также будет
изменяться. На одних частотах цепь будет носить активно-индуктивный характер,
на других активно-емкостный, а на некоторой частоте - называемой резонансной
частотой - чисто активный характер.
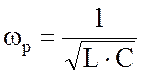
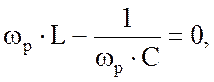 Резонансную
частоту легко определить из условия
Резонансную
частоту легко определить из условия
|
|
|
IIPИМEP l.8. К цепи, состоящей из последовательно соединенных катушки,
![]()
![]() индуктивности и конденсатора,
подключен источник э.д.с.
индуктивности и конденсатора,
подключен источник э.д.с.
В. Индуктивность катушки L - 2,55 мкГн, сопротивление обмотки Ом,
![]() емкость конденсатора С = 40 нФ, сопротивление потерь
конденсатора Ом, частота f - 500 кГц.
емкость конденсатора С = 40 нФ, сопротивление потерь
конденсатора Ом, частота f - 500 кГц.
Определить: 1) ток в цепи;
2) падение напряжения на элементах цепи;
3) построить векторную диаграмму;
Решение:
1. Начертим схему цепи и составим эквивалентную схему (рис. 1.53)
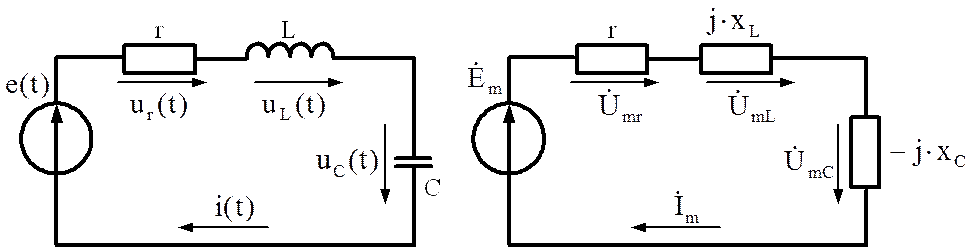 |
![]() Рис.1.53
Рис.1.53
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.