Линейные цепи в установившемся режиме: Курс лекций, страница 26

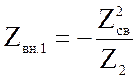где - вносимое сопротивление из второго контура в первый

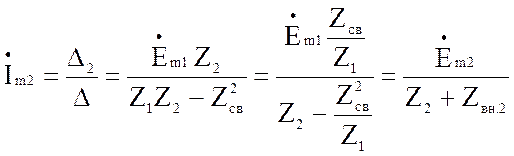  (4.47)

где 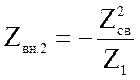- вносимое сопротивление из первого контура во второй

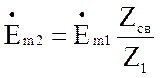 - э.д.с. второго контура, наводимая током первого контура

Эквивалентные схемы контуров, составленны по выражениям. 4.46 и 4.47, изображены на рисунки 4.35.

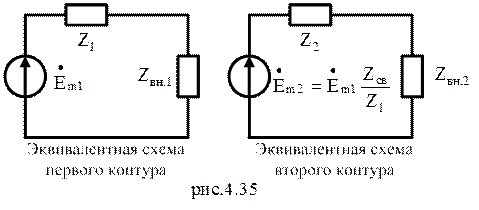
Рассмотрим более подробно вносимые сопротивления:

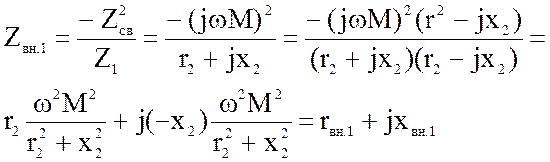  (4.48)

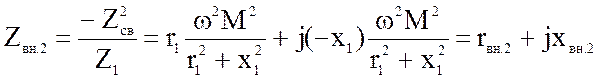 (4.49)

Вносимые сопротивления  учитывают взаимное влияние контуров:

 - учитывает потери энергии в 1-м контуре,  обусловленные
его связью со 2-м контуром,

 - учитывает потери энергии во 2-м контуре,  обусловленные его связью с 1-м контуром.

 и  представляют дополнительные реактивности, вносимые в один контур из другого.

Реактивный характер этих сопротивлении всегда противоположен характеру реактивного сопротивления контура, из которого вносится сопротивление. Эквивалентные схемы могут быть использованы для анализа процессов в контурах.

4.4.4. Частный и полный резонансы, настройка системы связанных контуров

Резонансом в системе связанных колебательных контуров называют явление, при котором имеет места максимум амплитуды тока или напряжения на элементах любого из контуров.

В связанных контурах могут быть следующие три вида резонансов.
1. Первый частный резонанс - при котором амплитуда тока в первом контуре максимальна.  Это возможно, когда суммарное реактивное сопротивление контура равно нулю:

                        (4.50)

При этом амплитуда тока в первом контуре равна:

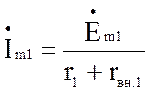
Настройку системы в первый частный резонанс осуществляют путем изменения С₁ или L₁ так, наступило равенство:

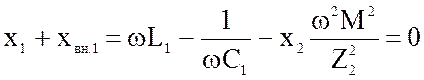        (4.51)

Это равенство является условием первого частного резонанса.

Примером использования первого частного резонанса служит настройка выходного колебательного контура радиопередатчика, индуктивно связанного с реактивной нагрузкой, например с антенной (рис.4.36).

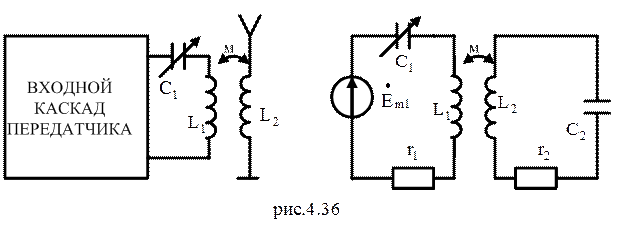
Пусть в приведенной схеме сопротивление второго контура имеет активно-емкостной характер. Это означает, что в первый контур из второго будет внесена некоторая индуктивность L_вн.1 . Чтобы настроить контур выходного каскада передатчика на рабочую частоту, необходимо несколько уменьшить индуктивность L₁ или емкость чтобы скомпенсировать увеличение суммарной индуктивности.

Признаком того,  что система настроена в первый частный резонанс может  служить максимум амплитуды э.д.с, взаимоиндукции,  наведенной в катушке L₂ за счет тока первого контура I_m1. Таким образом настройку системы контуров, в первый частный резонанс можно осуществить путем изменения первичных параметров первого контура  L₁ или   С₁.

2. Второй частный резонанс, при котором амплитуда тока во втором
контуре максимальна.

Это возможно,  когда суммарное реактивное сопротивление второго
контура равно нулю:

                         (4.52)

При этом значение амплитуды тока во втором контуре равно:

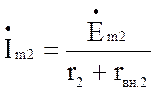
где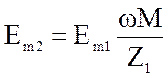

Настройку системы во второй частный резонанс осуществляют путем изменения L₂ или С₂ так, чтобы наступило равенство

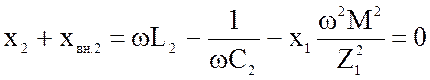          (4.53)

Это равенство является условием второго частного резонанса. Примером использования второго частного резонанса служит настройка колебательного контура во входной цепи радиоприемного устройства, индуктивно связанного с антенной (рис.4.37).

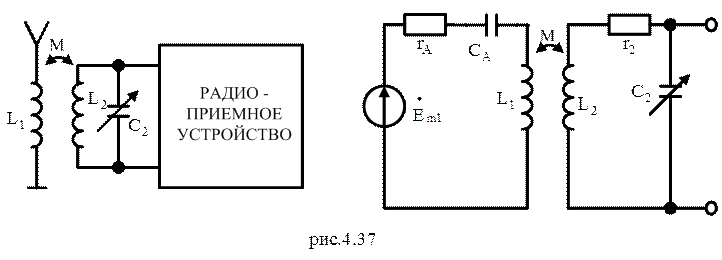
Первым контуром в данной схеме является антенная цепь, а вторым - перестраиваемый контур приемника. Пусть для приведенной схемы сопротивление первого контура носит активно-емкостный характер. Это означает, что во второй контур из первого будет внесена некоторая индуктивность L_вн.2. Чтобы настроить входной контур приемника на рабочую частоту, необходимо несколько уменьшить индуктивность L₂ или емкость С₂ чтобы скомпенсировать увеличение суммарной индуктивности.

 Признаком того, что система настроена во второй частный резонанс может служить максимум амплитуды напряжения на емкости С2. Таким образом, настройку  системы контуров во второй частный резонанс можно осуществить изменением первичных параметров второго контура L₂ или С₂.

3. Полный резонанс.

Полный резонанс в системе связанных контуров наступает тогда, когда оба контура, при отсутствии связи между ними, настроены в резонанс на одну и ту же частоту,  причем настройка такой системы в полный резонанс проводится путем увеличения связи до наибольшего значения амплитуды тока во втором контуре. При полном резонансе реактивные  сопротивления каждого из контуров равны нулю:

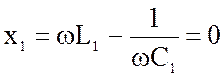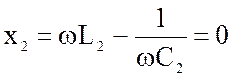  ;                    (4.54)

поэтому вносимые реактивные сопротивления также равны нулю:

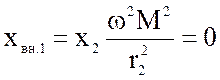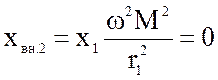  ;                  (4.55)

При полном резонансе оказываются выполненными условия первого и второго частных резонансов:

 ;                           (4.56)

Примером использования полного резонанса служит входная цепь радиоприемного устройства (рис.4.38).

радиоприемного устройства (рис.4.38)

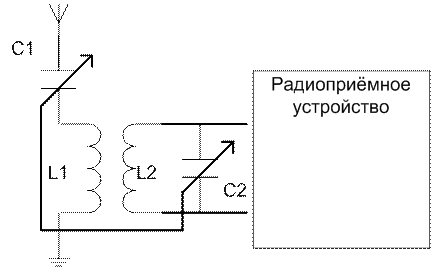
Рис. (4.38)

В приведенной схеме имеем два индуктивно-связанных контура с идентичными первичными параметрами L₁=L_2, C₁=C₂.

Каждый из этих контуров может быть настроен на заданную частоту путем одновременного изменения емкостей С₁ и С₂  находящимися на одном валу» Дальнейшая настройка системы в полный резонанс дости­гается путем изменения величины взаимной индуктивности до такой величины,  при которой амплитуда тока во втором контуре или напря­жение на емкости второго контура будет максимальным.

Амплитуда тока во втором контуре при произвольном значении взаимной индуктивности равна

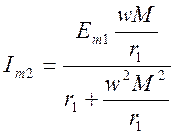                                                     (4.57)

Анализ показывает, что величина   lm₂(M)   достигает своего наи­большего значения

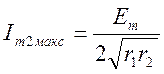                                                     (4.56)

при 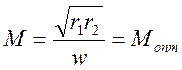                                                          (4.59)

      График зависимости lm₂(M) на рис.4.39 и называется настроечной кривой системы связанных контуров.

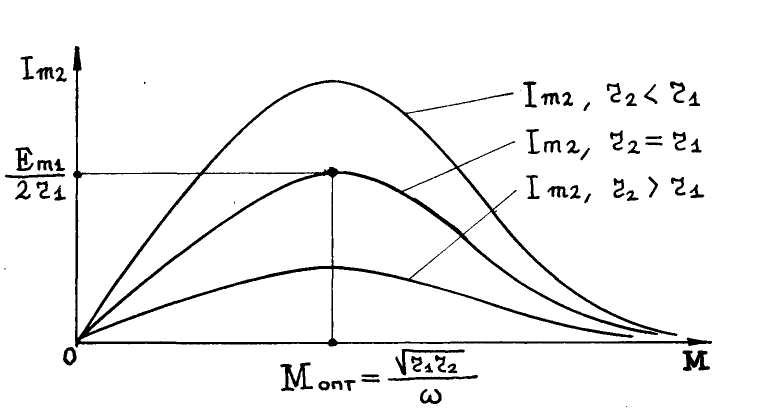
Рис.(4.39)