Электротехника \ Радиотехнические цепи и сигналы

Линейные цепи в установившемся режиме: Курс лекций, страница 31

При параллельном соединении четырехполюсников соответственно соединяются входные и выходные зажимы /рис.5.9/. Из рисунка вид­но, что входное и выходное напряжение исходных и результирующего четырехполюсника одинаковы. Таким образом, матрица полной проводимости результирующего че­тырехполюсника, полученного при параллельном соединении исходных четырехполюсников, равна сумме матриц полной проводимости этих четырехполюсников.

При последовательном соединении четырехполюсников соединяются последовательно соответственно входные и выходные зажимы /рис.5,9/*

Следовательно, матрица типа   Z   сложного четырехполюсника,  со­стоящего из последовательного соединения простых четырехполюсни­ков,  равна сумме матриц типа   "Z.   этих четырехполюсников.

Аналогично можно определить матрицу сложного четырехполюсника, состоящего из параллельно-последовательного или последовательно-параллельного соединения четырехполюсников. Правила нахождения матриц сложных четырехполюсников сведены в табл.5.3. Они справед­ливы при любом числе составных четырехполюсников. Однако правила сложения матриц применены только при резонансе токов входящего и выходящего в каждой паре выводов составных четырехполюсников,  которое может быть обеспечено тем или иным способом.  Соединение че­тырехполюсников, удовлетворяющее этому требованию, называется ре­гулярным.

Для вычисления элементов матриц сложных четырехполюсников не­обходимо знать матрицы простых четырехполюсников. Определим мат­рицы А- параметров для некоторых простейших четырехполюсников.

Напряжения и токи на входе ж на выходе равны между собой. Запишем это следующим образом:


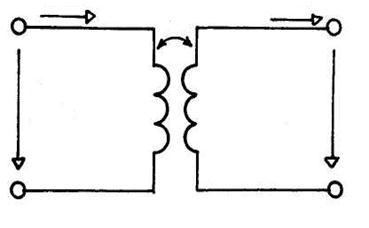
Идеальный трансформатор.


İm1
 

İ m2
 

M
 

Ům1
 
 


Рис. 5.13

Можно записать,  что        Ů m1=Ů m2·1/n+0·İ m2


Ům2
 
Пусть Ům2=nŮm1, а İ m2=İ m1·1/n. В этом случае имеет место равенство

Ů m1·İ m1= Ů m2·İ m2


                                                     İ m1=0·Ů m2+nİ m2                                                  (5.43)

Сравнивая уравнения (5.43) и (5.16), делаем вывод, что


  A11  A 12          1/n  0

  A21  A 22           0    n                                                                   (5.44)

где  n  - коэффициент трансформации.

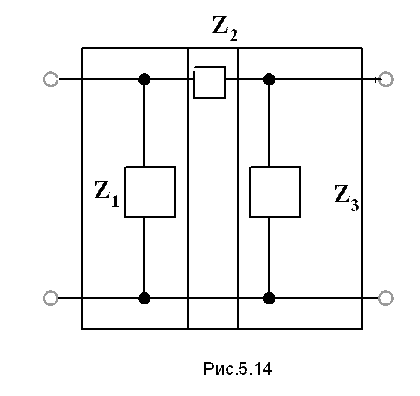
ПРИМЕР 5.1.   Определить матрицу А-параметров П-образного четырехполюсника,  если известны его элементы (рис.5.14).

РЕШЕНИЕ

П-образный четырехполюсник получен путем каскадного соединения трех простейших четырехполюсников    "б" - "а" - "б".
Матрица А-параметров может быть определена следующим образом

[A] = [A/] [A//] [A///] =

     1      0     1     z 2       1      0          1+z 2/z3                     z2

     1/z 1  1     0     1      1/z 3   1          1/z1+1/z3+z2/z1z3   1+z2/z2                   (5.45)

ПРИМЕР 5.2, Определить матрицу А-параметров Т-образного четырехполюсника, если известны все его элементы.


Т-образный четырехполюсник получен путем каскадного соединения трех простейших четырехполюсников "а" - "б" - "а".

Матрица А-параметров может быть определена следующим образом:

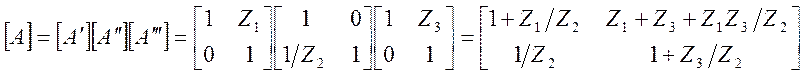       (5.46)

Матрицы других параметров Т-образного и П-образного четырехполюсников могут быть определены, исходя из выражении /5.31/ и (5.32), и с использованием формул связи, приведенных в таблице 5.1.

5.5. КОМПЛЕКСНЫЕ ВЫХОДНЫЕ ФУНКЦИИ НАГРУЖЕННОГО ЧЕТЫРЕХПОЛЮСНИКА

Рассмотренные ранее параметры четырехполюсников определяются только их схемами и параметрами их элементов, для анализа работы нагруженных четырехполюсников необходимо иметь больше информации.

Рис.5.16

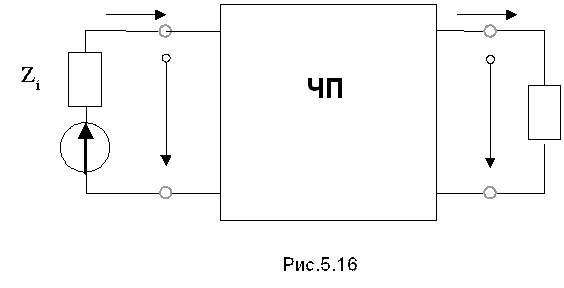
Как показано на рис.5.16 к четырех-полюснику подключены источник напряжения с внутренним сопротивлением Zi и сопротивление нагрузки Zн.

 (5.47)

 (5.48)
 
Система уравнений с А-параметрами имеет вид:

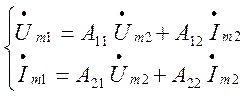
Комплексной входной функцией   Zвх.1 co стороны входных зажимов 1-1, при условии,  что к зажимам 2-2'подключено сопротивление Zh будет являться зависимость комллексного входного сопротивления от частоты.

Разделив выражение /5.47/ на /5.48/,  получим

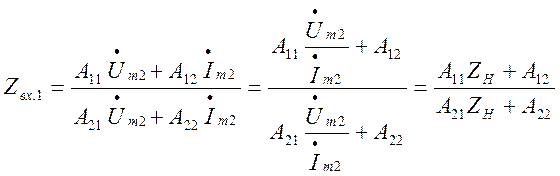                    (5.49)

Аналогично, комплексной входной функцией со стороны выходных зажимов 2-2', при условии, что к зажимам 1-1 подключено сопротивление Zi. , будет являться зависимость комплексного выходного сопротивления от частоты.

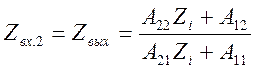                                            (5.50)

Как видно из выражений (5.49) и (5.50), входные сопротивления зависят не только от схемы и параметров четырехполюсника, но и от сопротивления нагрузки (внутреннего сопротивления источника). Таким образом,  четырехполюсник можно рассматривать как устройство для преобразования сопротивлении с целью согласования. Наиболее благоприятным режим передачи сигналов через  четырехполюсник является согласованный режим работы,  при котором сопротивление нагрузки и внутреннее сопротивление источника должны быть выбраны, исходя из условий

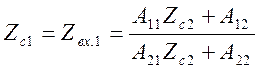                                           (5.51)

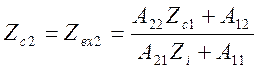                                           (5.52)

Решив систему уравнений (5.51) и (5.52) относительно неизвестных   Zc1 и   Zc2,  будем иметь;

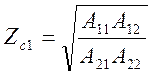                                                (5.53)

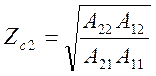                                                (5.54)

В выражениях /5.53/ и /5.54/ перед корнем всегда ставят знак "+", т.к. сопротивления пассивных цепей всегда имеют положительные вещественные части.

Скачать файл