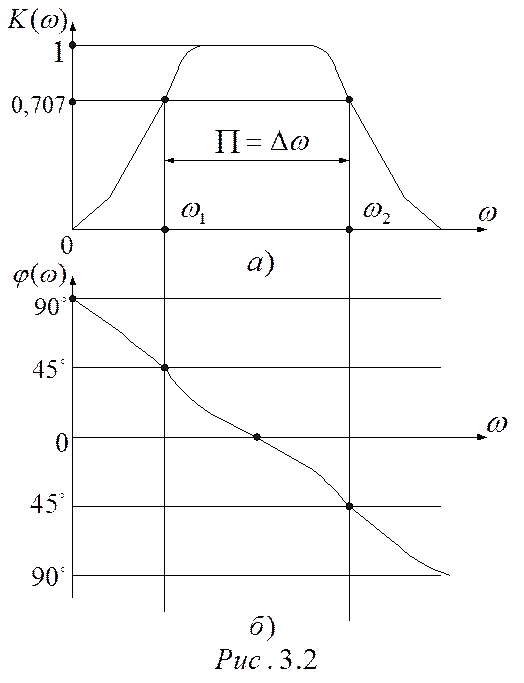 Полосой пропускания (
Полосой пропускания (![]() или
или
![]() ) называют область частот, в пределах
которой АЧХ уменьшается не более, чем в
) называют область частот, в пределах
которой АЧХ уменьшается не более, чем в ![]() раз
по сравнению с максимальным значением.
раз
по сравнению с максимальным значением.
Частоты ![]() и
и ![]() являются граничными частотами полосы
пропускания.
являются граничными частотами полосы
пропускания.
Используя графики (рис. 3.2)
можно определить значения ![]() для любой
заданной частоты, например:
для любой
заданной частоты, например:
для
![]()
![]() ;
;
для
![]()
![]() ;
;
для
![]()
![]() ;
;
Пусть на входе цепи с такими частотными свойствами действует синусоидальное напряжение:
![]()
при этом комплексная амплитуда входного напряжения равна:
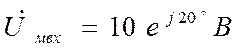
а комплексная амплитуда выходного напряжения:
![]()
Таким образом, синусоидальное напряжение на выходе цепи равно
![]()
Кроме показательной и алгебраической форм записи комплексных функций (3.8) часто применяют экспоненциальную форму записи:
![]() ,
,
где
![]() ;
;
![]() ; откуда
; откуда ![]() ;
;
![]() .
.
Функция ![]() называется
логарифмической амплитудно-частотной характеристикой (ЛАЧХ).
называется
логарифмической амплитудно-частотной характеристикой (ЛАЧХ).
Величина ![]() является
безразмерной и измеряется в неперах (Нп – единица измерения, применяемая в
технике проводной связи), белах и децибелах (дБ – единица измерения,
применяемая в радиолокации):
является
безразмерной и измеряется в неперах (Нп – единица измерения, применяемая в
технике проводной связи), белах и децибелах (дБ – единица измерения,
применяемая в радиолокации):
ПРИМЕР З.1:
а) Пусть амплитуда синусоидального
напряжения на выходе цепи в 10 раз больше амплитуды напряжения на входе. При
этом ![]() на данной частоте равен 10, тогда
значение ЛАЧХ на этой частоте равно:
на данной частоте равен 10, тогда
значение ЛАЧХ на этой частоте равно:
![]()
б) Пусть амплитуды синусоидальных
напряжений на входе и на выходе цепи равны, тогда ![]() .
.
При этом значение ЛАЧХ на данной частоте равно:
![]()
в) Пусть амплитуда синусоидального
напряжения на выходе цепи в 100 раз меньше амплитуды напряжения на входе, при
этом ![]() .
.
В этом случае значение ЛАЧХ на данной частоте равно:
![]()
ВОПРОСЫ:
1. Что называется АЧХ?
2. Что называется ФЧХ?
3. Что можно определить с помощью АЧХ и ФЧХ?
3.1.4. Способы определения частотных характеристик электрических цепей
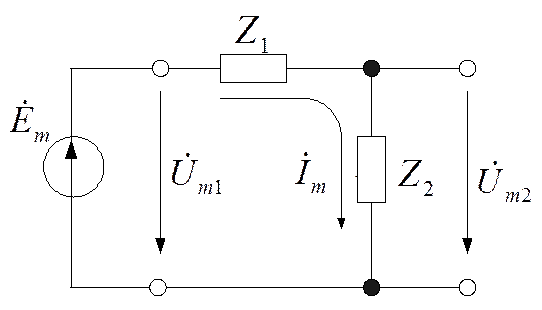 А. РАСЧЕТНЫЙ СПОСОБ
А. РАСЧЕТНЫЙ СПОСОБ
Для простых цепей (рис.3.3) аналитическое выражение, описывающее комплексную функцию получают, применяя законы Ома:
Рис. 3.3
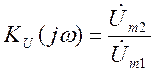 -
- по определению комплексной функции,
-
- по определению комплексной функции,
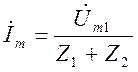 -
на основе закона Ома для замкнутого контура,
-
на основе закона Ома для замкнутого контура,
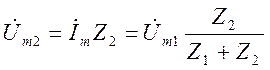 -
на основе закона Ома для участка цепи.
-
на основе закона Ома для участка цепи.
В итоге получим:
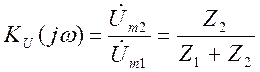 (3.13)
(3.13)
Чтобы получить аналитические выражения АЧХ и ФЧХ, выделяют модуль и аргумент:
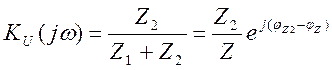 (3.14)
(3.14)
где
![]()
При этом
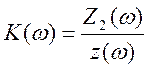 (3.15)
(3.15)
![]() (3.16)
(3.16)
Б. ЭКСПЕРИМЕНТАЛЬНЫЙ СПОСОБ
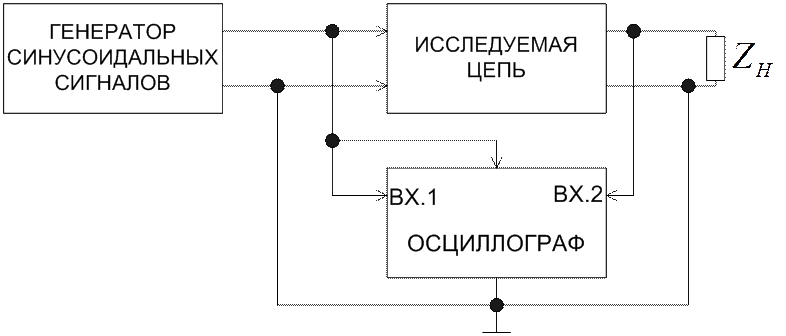
Рис. 3.4
На рисунке 3.4 приведена экспериментальная установка по исследованию частотных характеристик электрических цепей, по напряжению. Идея экспериментального способа становится понятной, исходя из следующих соображений. По определению комплексная передаточная функция по напряжению равна:
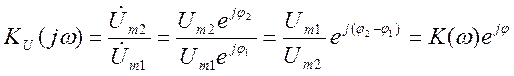
где
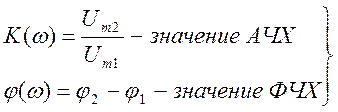 на заданной
частоте
на заданной
частоте
Следовательно, для исследования АЧХ и ФЧХ. необходимо проводить измерения амплитуд напряжений на входе и на выходе цепи, а также сдвигов фаз между напряжениями на входе и на выходе цепи на различных частотах в заданном диапазоне. Для измерения удобно применять двулучевой осциллограф. На первый вход осциллографа, подают входное напряжение, на второй вход - напряжение с выхода исследуемой цепи. Синхронизация работы осциллографа осуществляется входным напряжением с целью обеспечения возможности измерения сдвига фаз между входными и выходными напряжениями.
Изображение на экране осциллографа имеет вид приведенный на рисунке 3.5
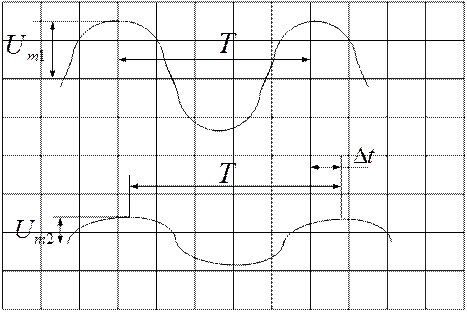
Рис. 3.5
Современные осциллографы имеют калибровку по амплитуде и по времени, поэтому, измеряя размеры изображения на экране осциллографа по вертикали и по горизонтали, можно измерить, амплитуды напряжений Um1, Um2, а также период колебаний Т и время задержки (или опережения) Δt выходного напряжения.
Зная Т и Δt, можно определить сдвиг по фазе в градусах:
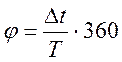 (град.)
(град.)
или в радианах:
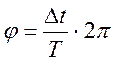 (рад.) (3.17)
(рад.) (3.17)
В ходе исследования экспериментальные данные сводят в таблицу.
|
Результаты измерений |
Результаты вычислений |
|||||
|
f |
Um1 |
Um2 |
|
T |
Um2/ Um1 |
|
Полученную таблицу используют для построения графиков АЧХ и ФЧХ.
3.2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПРОСТЫХ ЦЕПЕЙ
3.2.1. Частотные характеристики делителя напряжения
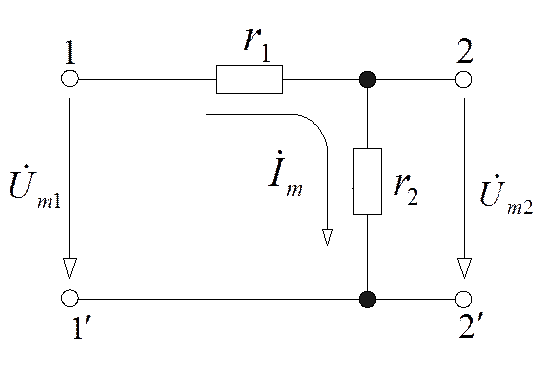
Делителем напряжения называется цепь, позволяющая снимать с выходных зажимов 2-2' некоторую часть напряжения, поданного на входные зажимы 1-1’ (рис.3.6).
Рис. 3.6
Комплексная передаточная функция по напряжению такой цепи равна:
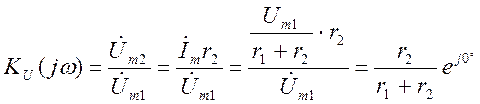 (3.18)
(3.18)
Отсюда
 - из этого
выражения видно, что АЧХ делителя напряжения не зависит от частоты.
- из этого
выражения видно, что АЧХ делителя напряжения не зависит от частоты.
![]() - ФЧХ делителя напряжения
также не зависит от частоты.
- ФЧХ делителя напряжения
также не зависит от частоты.
Графики АЧХ и ФЧХ приведены на рисунке 3.7.
 ВЫВОДЫ:
ВЫВОДЫ:
1. Напряжение на выходе делителя представляет собой часть входного напряжения, зависящую от соотношения между r1 и r2.
Если
![]() .
.
Если
![]() .
.
2. Напряжение на выходе совпадает по фазе с напряжением на входе.
3.2.2. Частотные характеристики интегрирующей цепи
Интегрирующими называются цепи, изображенные на pиc.3.8:
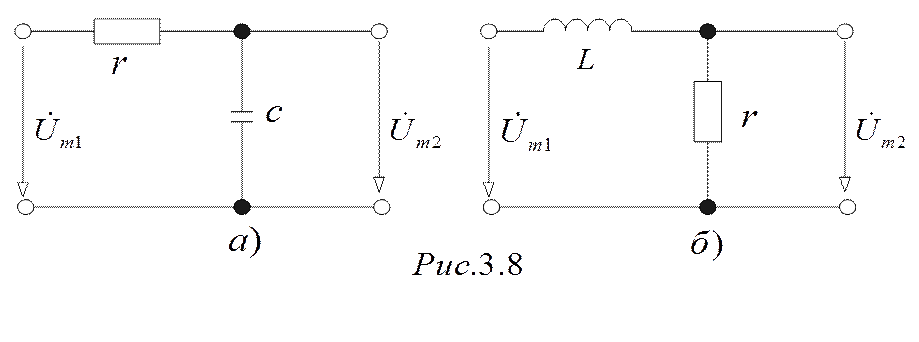
Комплексная передаточная функция по напряжению для схемы, изображенной
на рисунке 3.8а равна:
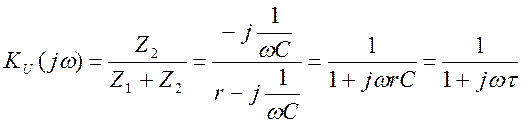 (3.19)
(3.19)
где
![]() - постоянная времени rC –
цепи.
- постоянная времени rC –
цепи.
Комплексная передаточная функция по напряжению для схемы, изображенной на рисунке 3.8б равна:
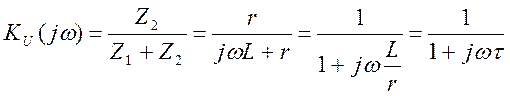 (3.20)
(3.20)
где
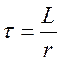 - постоянная времени rL –
цепи.
- постоянная времени rL –
цепи.
Таким образом, для обеих цепей:
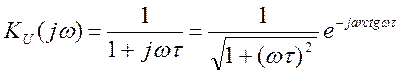 (3.21)
(3.21)
где
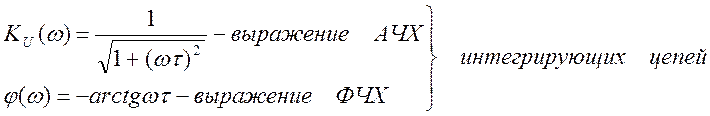
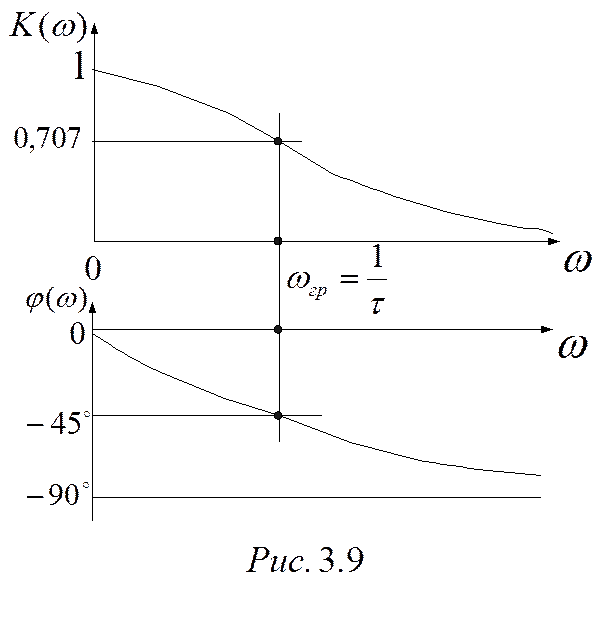 Графики АЧХ и ФЧХ интегрирующих цепей приведены на
рис.3.9. Область частот от 0 до
Графики АЧХ и ФЧХ интегрирующих цепей приведены на
рис.3.9. Область частот от 0 до 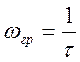 , является полосой
пропускания.
, является полосой
пропускания.
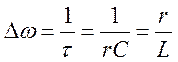 (3.22)
(3.22)
Ширину полосы пропускания можно изменять путем изменения
постоянной времени ![]() .
.
ВЫВОДЫ:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.