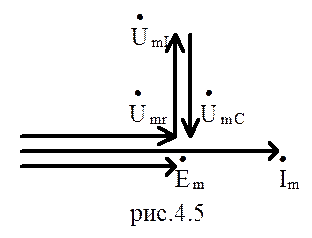 1. Ток, протекающий в контуре при
резонансе максимален и совпадает по фазе с приложенной Э.Д.С.
1. Ток, протекающий в контуре при
резонансе максимален и совпадает по фазе с приложенной Э.Д.С.
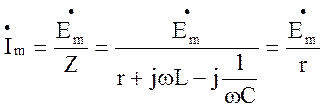 (4.4)
(4.4)
2. Напряжения на реактивных элементах контура при резонансе равны по амплитуде и противоположны по фазе и в раз больше э.д.с., действующей на контур:
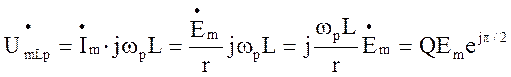 (4.5)
(4.5)
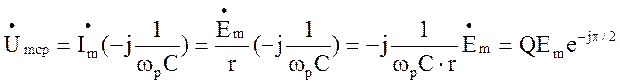 (4.6)
(4.6)
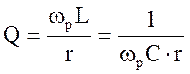 (4.7)
(4.7)
Векторная диаграмма тока в цепи и напряжений на элементах контура, соответствующая резонансу напряжений приведена на рисунки 4.5
ВОПРОСЫ:
1. Что называют резонансом напряжений?
2. Что является условием резонанса напряжений?
3. Что называется резонансной частотой?
4. Какие существуют признаки резонанса напряжений?
4.2.2. Основные параметры последовательного колебательного контура
Различают первичные и вторичные параметры контура.
К первичным параметрам относятся:
- индуктивность L , емкость С, активное сопротивление r.
К вторичным параметрам относятся:
резонансная частота, волновое или характеристическое сопротивление, добротность контура, затухание контура, полоса пропускания.
Резонансная частота характеризует величину частоты источника напряжения, при которой в контуре наступает резонанс напряжений:
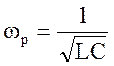
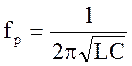 ;
;
Волновое или характеристическое сопротивление характеризует сопротивление реактивных элементов на резонансной частоте:
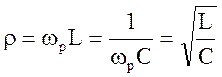
Добротность контура характеризует величину отношения волнового сопротивления к активному сопротивлению контура. Добротность контура показывает во сколько раз амплитуда напряжения на реактивных элементах больше амплитуды э.д.с. источника (формулы 4.5 и 4.6):
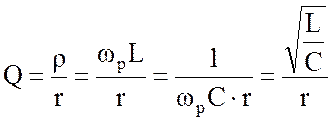
Затуханием контура называется величина обратная добротности:
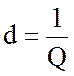
Добротность и затухание есть безразмерные величины. Для радиотехнических контуров характерны значения Q= 100 ÷ 500.
Полоса пропускания контура - это область
частот в пределах которой амплитуда напряжения на реактивных элементах
уменьшается не более чем в![]() раз по сравнению с
амплитудой напряжения на реактивных элементах на резонансной частоте. Полоса
пропускания связана с резонансной частотой и добротностью соотношением:
раз по сравнению с
амплитудой напряжения на реактивных элементах на резонансной частоте. Полоса
пропускания связана с резонансной частотой и добротностью соотношением:
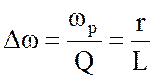 или
или 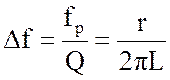
доказательство которого будет приведено.
ВОПРОСЫ:
1. Что относится к первичным параметрам?
2. Что относится к вторичным параметрам?
3. Что характеризует резонансная частота?
4. Что характеризует волновое сопротивление?
5. Что характеризует добротность контура?
6. Что такое полоса пропускания контура?
4.2.3. Настроенные кривые последовательного колебательного контура
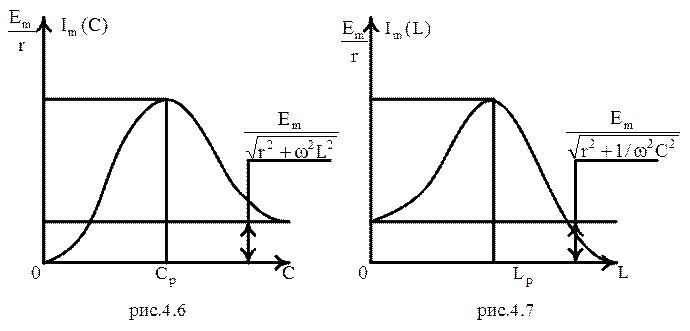
Настроечными кривыми называются зависимости амплитуды тока в контуре от величины емкости С и индуктивности L, т.е. Im.(c) или Im(L).
Для последовательного колебательного контура зависимость амплитуды тока от ω , L, С и r описывается выражением:
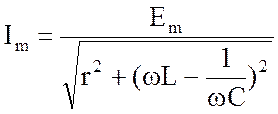 (4.8)
(4.8)
Пусть Еm, r, L и ω неизменны, найдем значения амплитуды тока при различных величинах емкости, данные сведем в таблицу:
|
C |
0 |
C=Cрез |
С=∞ |
|
Im(C) |
0 |
|
|
Пусть Еm, ω ,rи С неизменны, найдем значение амплитуды тока при различных величинах индуктивности, данные сведем в таблицу:
|
L |
0 |
L=Lp |
L=∞ |
|
Im(L) |
|
|
0 |
Графики настроечных кривых приведены на рисунки 4.6 и 4.7.
Кроме
представленных функций Im(C) и Im(L), могут рассматриваться следующие: Umc(C), Umc(L), Umc(C), UmL(L), которые могут быть
получены путем перемножения функций Im (С) или Im(L) на ![]() L или
L или ![]() .
.
4.2.4. Частотные характеристики последовательного колебательного контура
 Наиболее
часто в радиотехнике последовательный колебательный контур используется,
когда выходное напряжение контура снимается с емкости (рис.4.8)
Наиболее
часто в радиотехнике последовательный колебательный контур используется,
когда выходное напряжение контура снимается с емкости (рис.4.8)
Рассмотрим комплексную
передаточную функцию контура по напряжению: 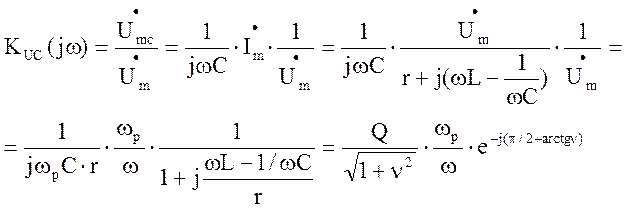 (4.9)
(4.9)
где 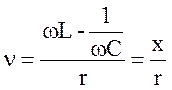 обобщенная
расстройка,
обобщенная
расстройка,
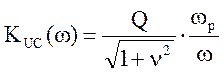 АЧХ контура (4.10)
АЧХ контура (4.10)
![]() ФЧХ контура (4.11)
ФЧХ контура (4.11)
Составим таблицу значений АЧХ и ФЧХ для некоторых характерных частот:
|
|
|
|
|
f |
|
0 |
1 |
0 |
|
0 |
|
|
0,707Q |
|
-1 |
|
|
|
Q |
|
0 |
|
|
|
0,707Q |
|
1 |
|
|
|
0 |
|
|
|
ПРИМЕЧАНИЕ. Значение АЧХ на нулевой частоте находят, из рассмотрения процессов в контуре на этой частоте. Пусть ω= 0, это значит, что на контур действует постоянное напряжение, при этом напряжение на выходе будет равно напряжению на входе, т.к. ток в контуре отсутствует и падение напряжения на элементах r и L равны нулю.
Для нахождения граничных частот полосы пропускания будем полагать ω =ωp.
На граничных частотах значения АЧХ будут в ![]() раз
меньше максимального значения, равного Q:
раз
меньше максимального значения, равного Q:
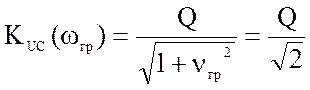 (4.12)
(4.12)
Это возможно при ![]() = ±1. Отсюда
= ±1. Отсюда
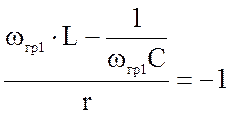 ;
;
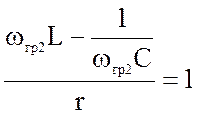 ;
;
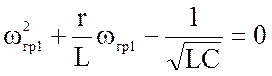 ;
;
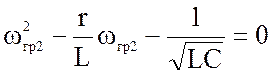 ;
;
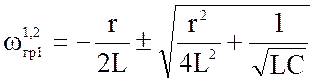 ;
; 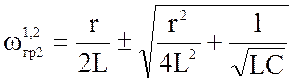 ;
;
Отрицательные значения частот ωrp.1 и ωrp.2 не имеют смысла, поэтому будем использовать в дальнейшем положительные значения граничных частот. Найдем полосу пропускания контура:
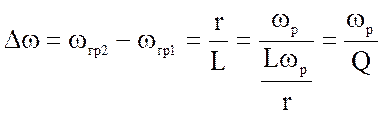 (4.13)
(4.13)
или 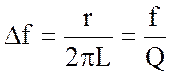
Как видно из приведенных выражений, ширина полосы пропускания контура не зависит от емкости C.
Значения граничных частот будем находить, полагая, что график АЧХ симметричен в области полосы пропускания:
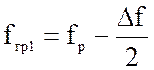 и
и 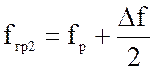 (4.14)
(4.14)
Построение графиков АЧХ и ФЧХ будем проводить, используя
данные, приведенные в таблице. С этой целью, сначала на частотных осях
откладывают значения характерных частот( f=0; fгр1 = fp - ![]() ;
; ![]() ;
; 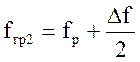 ;
; ![]() )
, затем по оси ординат откладывают соответствующие значения АЧХ и ФЧХ. Полученные
точки, соединяют плавной кривой (рис.4.9). При необходимости построения точных
графиков проводят предварительный расчет для большего числа точек на частотной
оси.
)
, затем по оси ординат откладывают соответствующие значения АЧХ и ФЧХ. Полученные
точки, соединяют плавной кривой (рис.4.9). При необходимости построения точных
графиков проводят предварительный расчет для большего числа точек на частотной
оси.
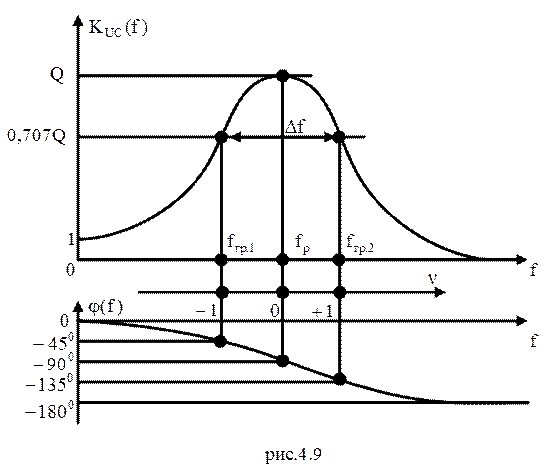
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.