Линейные цепи в установившемся режиме: Курс лекций, страница 18

Согласно второму закону Кирхгофа можно записать:

                      

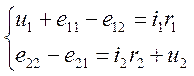
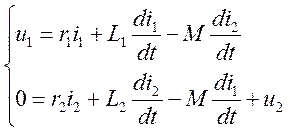
Эти уравнения называются уравнениями электрического равновесия трансформатора или просто уравнениями трансформатора.

Если к трансформатору приложено синусоидальное напряжение, то уравнение трансформатора в комплексной форме имеют вид:

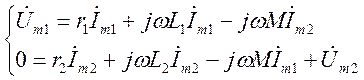
                                                        (2.18)

В зависимости от сопротивления нагрузки различают три режима работы трансформатора:

1)  - режим холостого хода;

2)  - режим нагрузки;

3)  - режим короткого замыкания.

В режиме холостого хода уравнения трансформатора принимают вид .

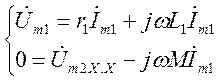                                                              (2.19)

Из второго уравнения следует , т.е. источником во вторичной обмотке является э.д.с. взаимоиндукции, создаваемая током первичной обмотки.

В разделе 1 были рассмотрены условия передачи максимальной активной мощности от источника в нагрузку:

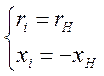                                                                              (2.20)

где     r_i, x_i - внутреннее активное и реактивное сопротивление источника;

r_H, x_H - активное и реактивное сопротивление нагрузки.

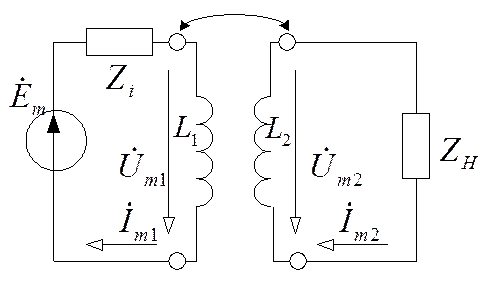Нагрузкой источника с заданным внутренним сопротивлением Z_i может быть существующее устройство с заданным сопротивлением Z_н. В таком случае согласование нагрузки с источником производится через согласующий трансформатор (рис. 2.20).

Потери в таком трансформаторе очень малы и для него справедливы соотношения.

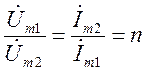
Рис. 2.20

где n- коэффициент трансформации.

Тогда входное сопротивление со стороны первичных зажимов:

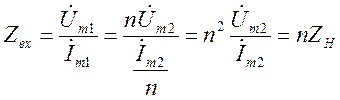
Т.е. согласующий трансформатор обладает свойством изменять полное сопротивление нагрузки в n² раз.

Свойствами, близкими к свойствам согласующего трансформатора, обладает трансформатор с магнитопроводом из высококачественного магнитного материала при достаточно большом числе витков его обмоток.

ВОПРОСЫ:

1.  Что называется трансформатором?

2.  Что называется первичной обмоткой? Вторичной?

3.  Сформулируйте уравнения трансформатора.

3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

3.1. ОБЩИЕ ПОНЯТИЙ И ОПРЕДЕЛЕНИЯ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

3.1.1. Комплексные функции электрических цепей

Основным методом расчета процессов в цепях синусоидального тока является метод комплексных амплитуд, при этом синусоидальные функции представляют следующим образом:

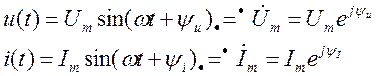                                                   (3.1)

Для цепи, приведенной на рисунке 3.1 на входе и на выходе действуют синусоидальные токи и напряжения. Можно сказать, что на входе цепи действуют синусоидальные воздействия  или , которые обозначим .

Рис.3.1

При этом, на входе и на выходе цепи будут иметь место синусоидальные реакции  или  и или  на какой-либо входное воздействие. Реакцию цепи обозначим 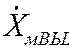. Другими словами,  может быть причиной возникновения , , , a  может быть причиной возникновения , , .

Комплексной функцией цепи называют отношение реакции цепи к воздействию, заданным в виде комплексных амплитуд:

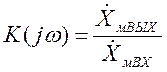                                                                                (3.2)

С помощью комплексной функции легко найти комплексную амплитуду выходного сигнала как произведение:

                                                                        (3.3)

3.1.2. Комплексные входные и передаточные функции

В зависимости от того, рассматривается ли реакция цепи со стороны точек приложения воздействия или же на других участках различают комплексные входные функции цепи и комплексные передаточные функции цепи.

Комплексными входными функциями называют отношения комплексных амплитуд тока и напряжения, действующих на входных зажимах цепи (рис.3.1).

В зависимости от того, какая величина является воздействием различают входное сопротивление и входную проводимость:

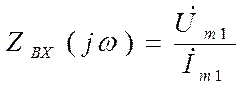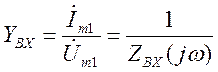;                                      (3.4)

Комплексными передаточными функциями называют отношения комплексных амплитуд токов и напряжений, действующих на разных парах зажимов (рис.3.1).

В зависимости оттого, что является воздействием, различают:

а) комплексные передаточные функции по напряжению и по току:

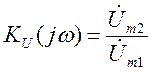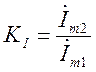;                                                (3.5)

б) передаточные сопротивления:

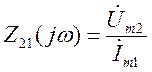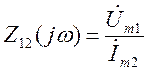;                                         (3.6)

в) передаточные проводимости:

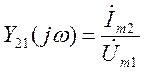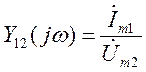;                                          (3.7)

ВОПРОСЫ:

1.  Что называется комплексными входными функциями?

2.  Что называется комплексными передаточными функциями?

3.1.3. Частотные характеристики электрических цепей

Комплексные функции цепи представляют отношения комплексных амплитуд токов и напряжений, действующих на входе и на выходе при синусоидальном воздействии. Как и любые комплексные числа их можно выразить в показательной форме записи (через модуль и аргумент) или в алгебраической форме записи через вещественную и мнимую части:

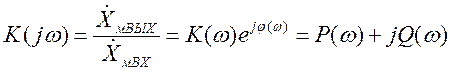                                                   (3.8)

где 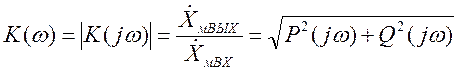   ;                                                 (3.9)

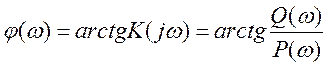;                                                                 (3.10)

;                                                              (3.11)

;                                                               (3.12)

Выражения (3.9 - 3.12) показывают связь между параметрами алгебраической и показательной форм записи комплексных функций. Амплитудно-частотной характеристикой (АЧХ) называют зависимость модуля  от частоты. Величина  определяет отношение амплитуды реакции цепи к амплитуде воздействия.

Фазо-частотной характеристикой (ФЧХ) называют зависимость аргумента  от частоты. Величина  определяет сдвиг по фазе реакции относительно воздействия.

Частотные характеристики (АЧХ и ФЧХ) описывают свойства цепей при воздействии синусоидальных сигналов. С их помощью можно определить реакцию цепи на заданное воздействие любой частоты, а также судить о важных особенностях и возможностях использования цепи. Например, АЧХ приведенная на рисунке 3.2а, характеризуем цепь, способную пропускать сигналы только в диапазоне частот от до