Электротехника \ Радиотехнические цепи и сигналы

Линейные цепи в установившемся режиме: Курс лекций, страница 16


откуда                     


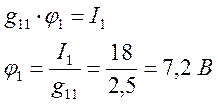
Токи в ветвях равны:

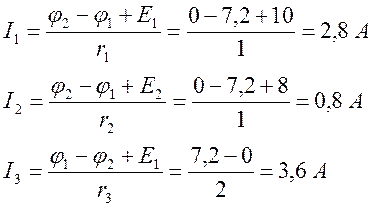
ВОПРОСЫ:

1.  Для каких электрических цепей применяется метод?

2.  В чем состоит сущность метода?

3.  Что такое собственная проводимость узла?

4.  Что такое взаимная проводимость между узлами?

5.  Что такое узловой ток?

2.1.5. Метод наложения

Метод наложения основан на принципе наложения, сущность которого заключается в том, что в любой  ветви линейной электрической цепи,   содержащей несколько источников э.д.с., рассматривают как алгебраическую сумму так называемых частичных токов, созданных в этой ветви действием каждой э.д.с. в отдельности.

Сущность метода наложения состоит:

1) в расчете частичных токов в ветвях для каждого источника в отдельности;

2) в алгебраическом суммировании частичных токов каждой ветви.

ПРИМЕР 2.3.

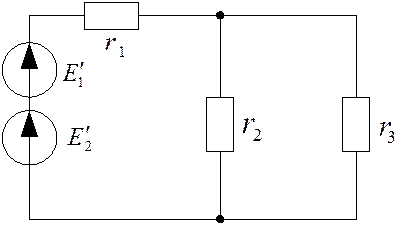
    Дано:

    В; B;

      Ом; Ом;

       Ом.

      Найти токи в ветвях.

Рис. 2.5

РЕШЕНИЕ: Для определения частичных токов в ветвях необходимо провести столько частных расчетов, сколько источников э.д.с. в схеме.

1. Первый частный расчет:


Исключим из суммы источник  э.д.с.. Получим схему, изображенную на рис. 2.6. Любым изученным методом рассчитаем токи в ветвях.


Рис. 2.6

Применим метод эквивалентных преобразований. Сопротивление  и, включенные параллельно, заменим эквивалентным сопротивлением , получим схему, изображенную на рисунке 2.7. Для расчета тока в такой цепи применим закон Ома для замкнутого контура.

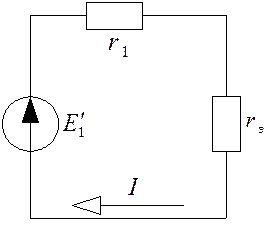
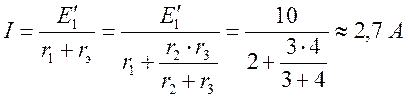
     Рис. 2.7

Чтобы определить токи через сопротивления  и  надо сначала определить падение напряжения на них:


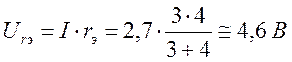
Ток через сопротивление  равен:

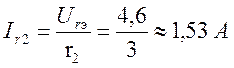
аналогично

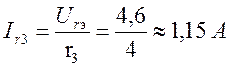
Обозначим

 ;  ;

2. Второйчастый расчет:

Исключим из схемы источник э.д.с.  получим схему, аналогичную изображенной на рисунке 2.6. Исходя из того, что 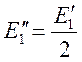 частичные токи равны:

 ;  ;  .

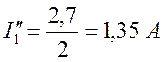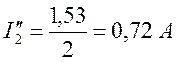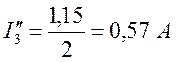Токи в ветвях будут равны алгебраической сумме частичных токов:

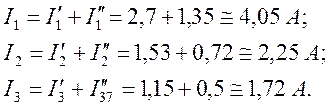
Если бы источник , был бы направлен в противоположную сторону, то алгебраические суммы частичных токов были бы равны:

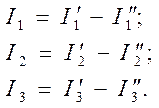
2.1.6. Методы эквивалентного генератора

Данный метод применяют тогда, когда требуется найти ток в одной из ветвей электрической цепи.

Сущность метода состоит:

1)  в замене сложной электрической цепи, к которой подключена интересующая нас ветвь, эквивалентным ее источником напряжения;

2)  в расчете искомого тока согласно закона Ома для замкнутого контура.

Пусть имеем электрическую схему, изображенную на рисунке 2.8.

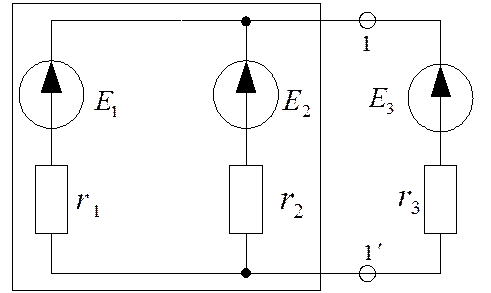
Требуется найти ток в третьей ветви.
Если представить левую часть схемы
(относительно зажимов 1-1) в виде эквивалентного ей источника напряжения, то схема будет иметь вид, представленный на рис. 2.9.

Рис.2.8

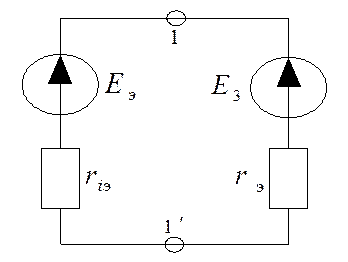
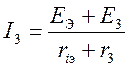Ток в третьей ветви можно найти по закону Ома для замкнутого
контура                                         (2. 8)

если знать параметры эквивалентного генератора-источника напряжения: - эквивалентную э.д.с. и - эквивалентное внутреннее сопротивлении. Эти  параметры определяют следующим образом:

Рис. 2.9

а) определение эквивалентной э.д.с. . Для того, чтобы определить

необходимо найти напряжение на зажимах 1-1' в режиме холостого хода (рис. 2.10).

Рассчитаем ток холостого хода:

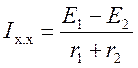                                                    (2.9)

Определим напряжение на зажимах :

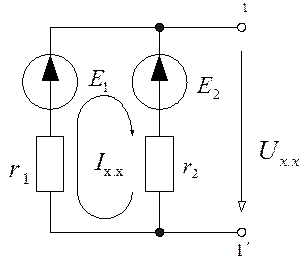
                                        (2.10)

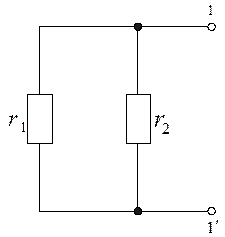
б) определение эквивалентного внутреннего

сопротивления. Для того, чтобы найти внутреннее сопротивление эквивалентного генератора, необходимо исключить из схемы источники э .д. с. Е1 и Е2 и заменить их перемычками, как это показано на рисунке 2.11, a затем найти сопротивление между зажимами :

          Рис. 2.10

                                               (2.11)

Рис. 2.11

2.1.7. Принцип взаимности

Принцип взаимности утверждает, что если э.д.c. Е, действуя в ветви аb сколь угодно сложной электрической цепи, не содержащей других источников э.д.с. (pиc. 2.l2a), вызывает в ветви cd некоторый ток I, то эта же э.д.с., действуя в ветви cd вызовет в ветви ab такой же ток I (pиc. 2.12б).

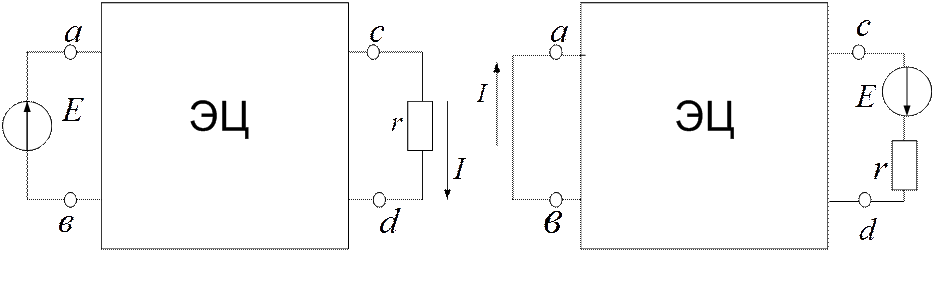
а                                                                     б

Рис. 2.12

2.1.8. Применение методов расчета электрических цепей синусоидального тока

В разделе 1 было показано, что уравнения, выражающие законы Кирхгофа в комплексной форме для цепей синусоидального тока, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока, только токи, напряжения э.д.с. и сопротивление входят в уравнения в виде комплексных величин.

Рассмотренные ранее методы применительно к цепям постоянного тока получены на основе законов Кирхгофа. Следовательно, для цепей синусоидального тока можно обосновать те же методы, которые были получены для цепей постоянного тока.

Поэтому в том случае, когда отдельные ветви электрической цепи синусоидального тока не связаны между собой магнитно, все расчетные формулы рассмотренных методов пригодны для цепей синусоидального тока, если в этих формулах заменить:

постоянный ток - комплексной амплитудой тока;

постоянную э.д.с. - комплексной амплитудой э.д.с;

постоянный узловой потенциал - комплексной амплитудой узлового потенциала;

сопротивление - комплексным сопротивлением;

проводимость - комплексной проводимостью.

Например, система уравнений при расчете схемы рис.2.3 по методу контурных токов с учетом того, что в цепи действуют синусоидальные э.д.с, примет вид:

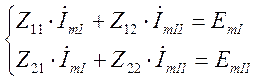
При расчетах цепей постоянного тока искомые токи получаются отрицательными, когда действительное направление тока или напряжения не соответствуют выбранным условно.

При расчетах цепей синусоидального тока действительное направление  синусоидального тока периодически изменяется, поэтому произвольность выбора условного положительного направления отражается только на фазе. Изменение выбранного положительного направления на противоположное меняет фазу на 180°, что соответствует изменению знака комплексной амплитуды тока и изменению на противоположное направление вектора на векторной диаграмме.

Скачать файл