Для схемы на рис.2.2 это ![]()
2) Контурная э.д.с. - алгебраическая сумма э.д.с. данного контура
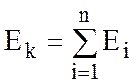 |
|||
|
|||
Если э.д.с, рассматриваемого контура совпадают с направлением контурного тока, то знак (+), если противоположны ему – знак (-).
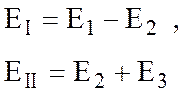 |
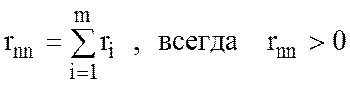 3) Собственное сопротивление контура - сумма
всех сопротивлений, входящих
в рассматриваемый контур.
3) Собственное сопротивление контура - сумма
всех сопротивлений, входящих
в рассматриваемый контур.
![]() В нашей схеме:
В нашей схеме:
![]() 4) Взаимное сопротивление
контуров - сопротивление ветви, входящей одновременно в два разных контура
4) Взаимное сопротивление
контуров - сопротивление ветви, входящей одновременно в два разных контура
|
для схемы на рис.2.2: |
Взаимное сопротивление имеет знак "+", если контурные токи в общей совпадают и наоборот.
Упрощение, достигаемое введением понятия контурных токов, не ограничивается уменьшением числа уравнений, оно определяется еще и тем, что достигается некоторым автоматизм в записи системы уравнении. Система уравнении может быть записана без рассмотрения контурных токов цепи, необходимо лишь выяснить количество независимых контуров.
В общем случае для n независимых контуров
![]()
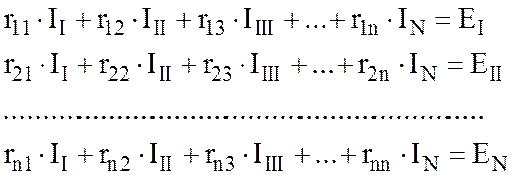 |
|||
|
|||
![]()
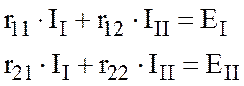
Решая систему уравнений, находят контурные токи. Если один из контурных токов имеет отрицательное значение, то истинное направление контурного тока противоположно условно выбранному.
Решение задачи не заканчивается определением контурных толов.
По контурным токам необходимо найти токи в ветвях. Если в ветви протекает только один контурный ток, то ток в ветви совпадает по направлению и равен по значению контурному току.
Токи в ветвях, по которым протекает несколько контурных токов, равны их алгебраической сумме, направление тока в такой ветви совпадает с большим контурным током. В рассматриваемой схеме:
I1=II;
I2=III-II (III>II); I2=II-III (III<II);
I3=III;
Алгоритм расчета цепей методом контурных токов
1) Определить число ветвей "b"
и узлов "у".
2) Выбрать n2 =b – (y-1) независимых контура.
4. В результате решения системы
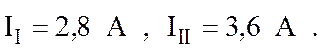 |
5. Токи в ветвях
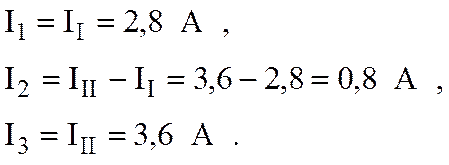 |
ВОПРОСЫ:
1. В чем состоит сущность метода?
2. Что такое контурный ток?
3. Что такое контурная ЭДС?
4. Что такое собственное сопротивление контура?
5. Что такое взаимное сопротивление контуров?
2.1.4. Метод узловых потенциалов
Метод применим для расчета любых электрических цепей. Сущность метода состоит:
1) В составлении системы уравнении согласно первому закону Кирхгофа;
2) В решении полученной системы;
3) В определении товаров в ветвях по закону Ома для
участков цепи с пассивными или активными элементами;
Рассмотрим цепь (рис.2.4). Введем ряд понятия.
1) Узловой
потенциал – напряжение между узлами схемы и опорным (базисным) 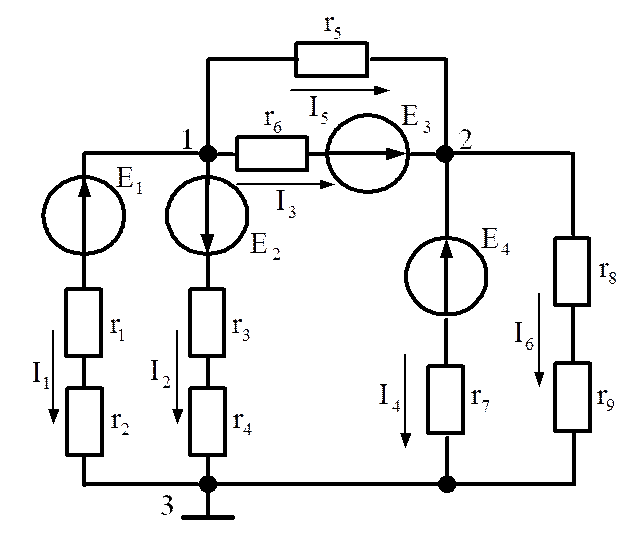 узлом.
узлом.
2) Опорный узел выбирается произвольно, потенциал опорного узла полагается равным нулю (узел заземляется).
3) Остальные узлы нумеруются
последовательно.
Заземлим узел 3 (j3 = 0).
|
2) Собственная проводимость узла - сумма проводимостей всех ветвей, соединенных с данным узлом.
![]()
В схеме на рис.2.4
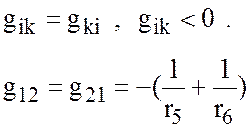 3) Взаимная
проводимость между узлами - сумма проводимостей ветвей, соединяющих эти узлы
3) Взаимная
проводимость между узлами - сумма проводимостей ветвей, соединяющих эти узлы
|
4) Узловой ток - алгебраическая сумма токов всех ветвей с активными элементами, сходящимися в узле.
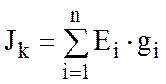 (2.6)
(2.6)
|
где |
JK - узловой ток k-того узла;
Ei - Э.Д.С. i-той ветви;
gi - проводимость i-той ветви;
Ток ветви берется со знаком "+", если э.д.с направлены к узлу, со знаком "-" - от узла. В рассматриваемой схеме:
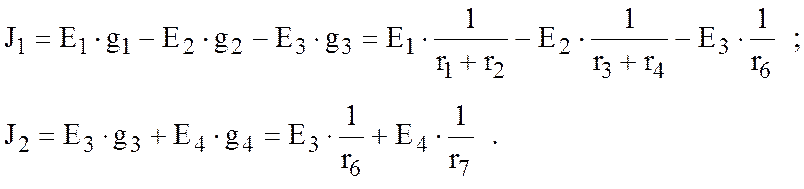 |
Система уравнений составляется относительно узловых потенциалов по известному числу независимых узлов n1= у - 1.
В общем случае
|
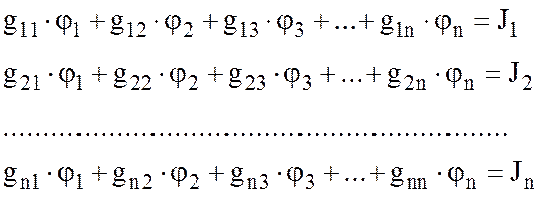
В схеме на рис.2.4:
![]()
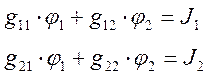
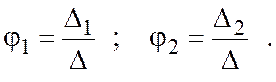 Решив данную систему относительно
неизвестных потенциалов методом определителей, можно получить:
Решив данную систему относительно
неизвестных потенциалов методом определителей, можно получить:
Зная величины потенциалов узлов, можно найти токи между ними, используя закон Ома для пассивного участка для 5-и и 6-и ветвей и закон Ома для участка с активными и пассивными элементами для 1-й, 2-Е и 4~й
![]() ветвей. Направление токов в ветвях будем
выбирать от большего узлового потенциала к наименьшему. Пусть,
например, , тогда токи в ветвях будут течь в
направлениях, как показано на рис.2.4.
ветвей. Направление токов в ветвях будем
выбирать от большего узлового потенциала к наименьшему. Пусть,
например, , тогда токи в ветвях будут течь в
направлениях, как показано на рис.2.4.
Применим закон Ома для расчета токов:
|
|
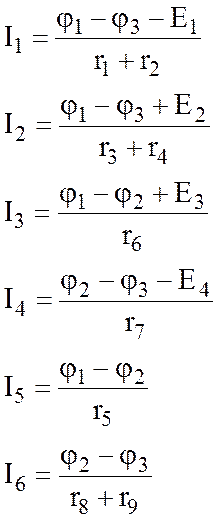
АЛГОРИТМ РАСЧЕТА МЕТОДОМ УЗЛОВЫХ ПОТЕНЦИАЛОВ
1)
Заземлить один узел, потенциал
которого от этого станет равным нулю, пронумеровать остальные узлы.
2) Вычислить узловые токи согласно
(2.6).
3) Вычислить
собственные и взаимные проводимости узлов.
4) Составить
систему уравнении вида (2.7) и решить ее, при этом будут найдены узловые потенциалы.
5) Найти токи в
ветвях по закону Ома.
ПРИМЕР 2.2: для электрической цепи пример 2.1 найти токи в ветвях методом узловых потенциалов.
РЕШЕНИЕ:
Заземлим нижний узел, а верхний будем считать первым. Найдем узловой ток верхнего (первого) узла:
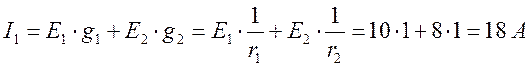
Собственная проводимость первого узла:

Так как других узлов у данной схемы нет, то система уравнений будет представлять собой лишь одно уравнение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.