б) умножение на положительное число:
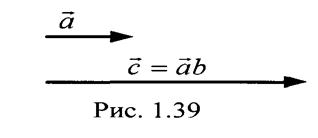 при этом исходный вектор "а" растягивается в
"b" раз (рис. 1.39).
при этом исходный вектор "а" растягивается в
"b" раз (рис. 1.39).
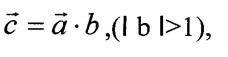 в)
умножение на отрицательное число:
в)
умножение на отрицательное число:
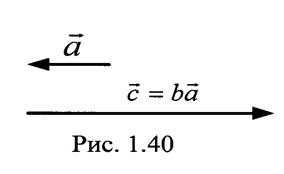 при этом исходный вектор "а" растягивается в
о раз и поворачивается на 180° (рис.1.40).
при этом исходный вектор "а" растягивается в
о раз и поворачивается на 180° (рис.1.40).
![]() г) умножение на
г) умножение на
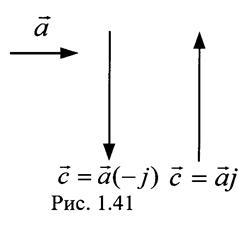 при этом исходный вектор поворачивается соответственно на +90°
(рис.1.41).
при этом исходный вектор поворачивается соответственно на +90°
(рис.1.41).
Другие действия с векторами встречаются реже, поэтому ми их не рассматриваем. Полезно запомнить следующие соотношения:
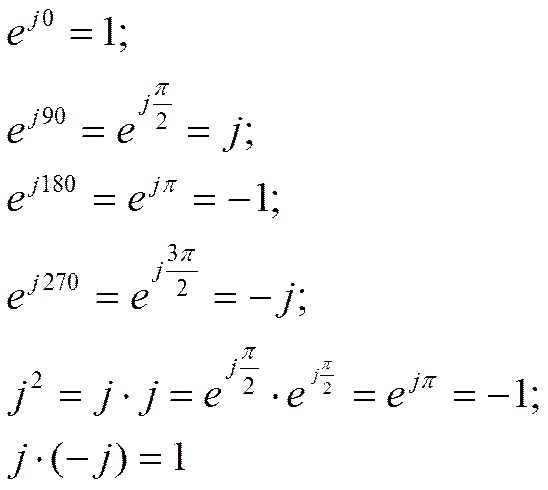 |
1.5. ЗАКОНЫ OМА И КИРХГОФА ДЛЯ МГНОВЕННЫХ И КОМПЛЕКСНЫХ ЗНАЧЕНИЙ ТОКА И НАПРЯЖЕНИЯ
1.5.1. Основные законы электротехники для мгновенных и комплексных значений электрических величин
![]()
![]() Если к электрической цепи (рис.1.42а) приложить
синусоидальное напряжение , то в
цепи потечет ток
Если к электрической цепи (рис.1.42а) приложить
синусоидальное напряжение , то в
цепи потечет ток
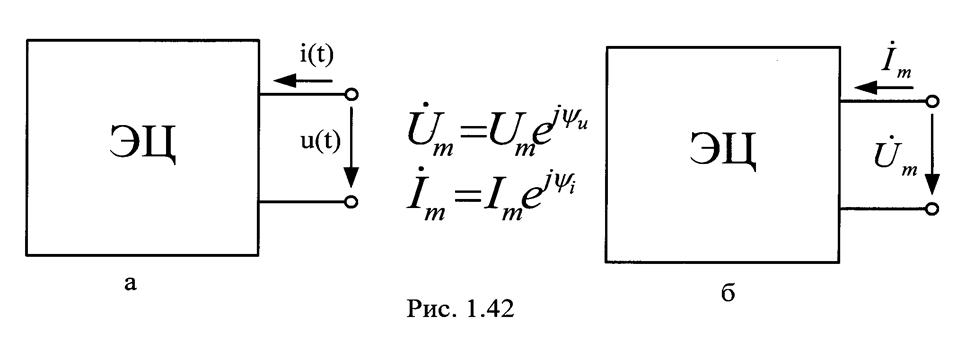
Перейдем к изображению синусоидальных величин комплексными амплитудами (рис. 1.42б).
Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется комплексным сопротивлением
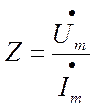 |
(1.32)
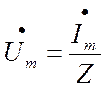
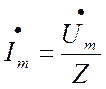 Выражение (1.32) представляет собой закон Ома в
комплексной форме. Его можно записать в виде
Выражение (1.32) представляет собой закон Ома в
комплексной форме. Его можно записать в виде
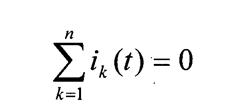 Учитывая,
что сложению синусоидальных величин – оригиналов –соответствует сложение
изображений – комплексных амплитуд, то на основании первого закона Кирхгофа
для мгновенных значение токов
Учитывая,
что сложению синусоидальных величин – оригиналов –соответствует сложение
изображений – комплексных амплитуд, то на основании первого закона Кирхгофа
для мгновенных значение токов
получим выражение для этого закона в комплексной форме
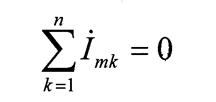 |
(1.33)
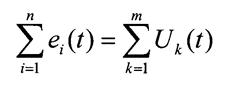 Аналогично
второй закон Кирхгофа для мгновенных значении э.л.с. и напряжений
Аналогично
второй закон Кирхгофа для мгновенных значении э.л.с. и напряжений
и в комплексной форме
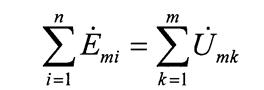 |
(1.34)
Из выражений для закона Ома и законов Кирхгофа видно, что запись этих законов в комплексной (форме аналогична записи этих законов для цепей постоянного тока. Поэтому все методы расчета цепей постоянного тока можно применять к расчету цепей переменного тока.
1.5.2. Комплексные сопротивления и проводимости в цепях синусоидального тока
Рассмотрим комплексное сопротивление (1.32)
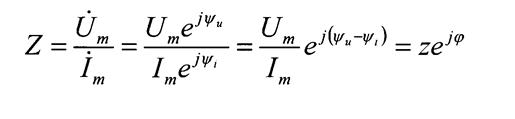 |
(1.35)
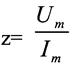 |
- модуль комплексного сопротивления,
-
![]() аргумент комплексного сопротивления, равный сдвигу фаз между напряжением
и током
аргумент комплексного сопротивления, равный сдвигу фаз между напряжением
и током
Примения формулу Эйлера:
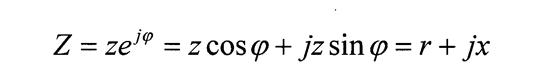 |
(1.36)
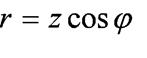 - активное сопротивление;
- активное сопротивление;
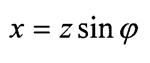 - реативное сопротивление
- реативное сопротивление
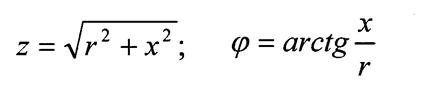 (1.37)
(1.37)
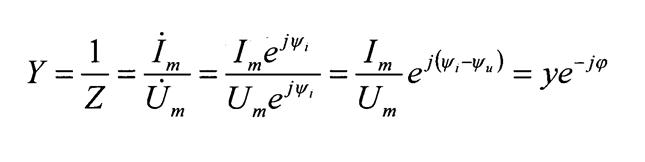 Комплексная
величина Y, обратная комплексному сопротивлению Z, называется
комплексной проводимостью.
Комплексная
величина Y, обратная комплексному сопротивлению Z, называется
комплексной проводимостью.
(1.38)
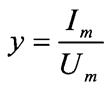 |
- модуль комплексной проводимости.
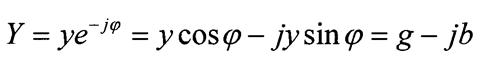 |
(1.39)
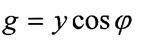 |
- активная проводимость,
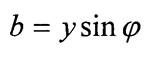
- реактивная проводимость.
1.5.3. Цепи синусоидального тока с одним
пассивным элементом. Цепь синусоидального тока с активным 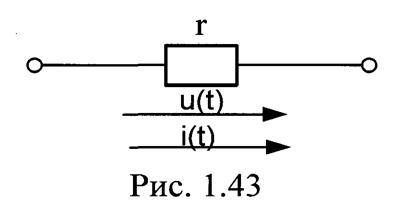 сопротивлением
сопротивлением
 Рассмотрим цепь, изображенную на рис.1.43. Подключим к данной цепи
синусоидальное напряжение.
Рассмотрим цепь, изображенную на рис.1.43. Подключим к данной цепи
синусоидальное напряжение.
Под действием этого напряжения по цепи потечет синусоидальный ток
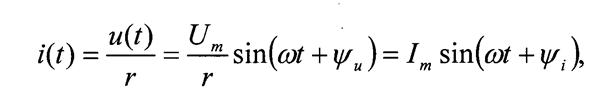 |
|||
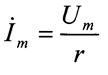 |
|||
- амплитуда тока;
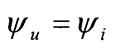 -
начальная фаза тока.
-
начальная фаза тока.
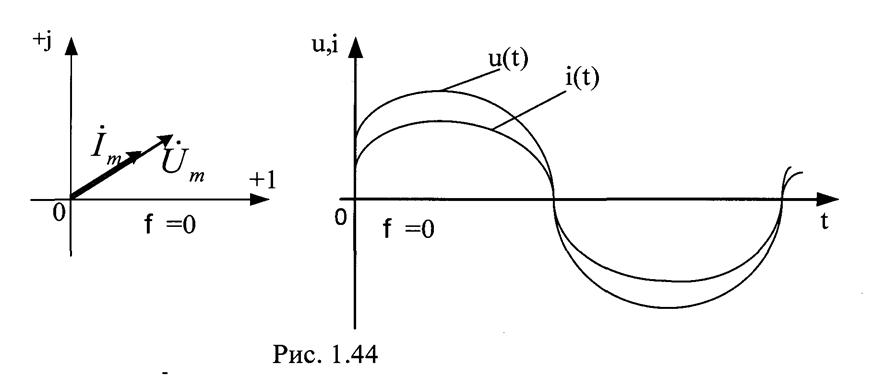
Таким образом, в цепи синусоидального тока с одним активным сопротивлением напряжение и ток совпадают по фазе.
Векторная и развернутая диаграмма для этого случая изображены на рис.1.44
 |
Комплексное сопротивление цепи
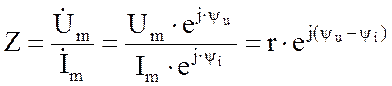 (1.40)
(1.40)
является вещественной величиной.
ЦЕПЬ СИНУСОИДАЛЬНОГО ТОКА С ИНДУКТИВНОСТЬЮ
Если к индуктивности (рис.1.45) подключить синусоидальное напряжение u(t), то по ней потечет ток
![]()

|
![]()
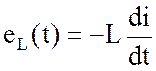
|
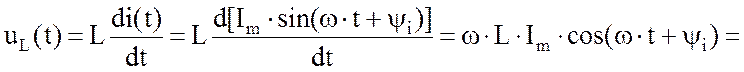
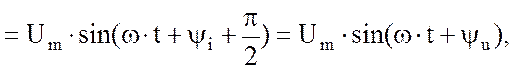 Отсюда
Отсюда
![]() где - амплитуда напряжения,
где - амплитуда напряжения,
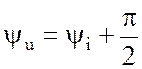 - начальная фаза напряжения.
- начальная фаза напряжения.
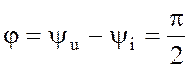 Сдвиг фаз между напряжением и током в цепи с
индуктивностью равен
Сдвиг фаз между напряжением и током в цепи с
индуктивностью равен
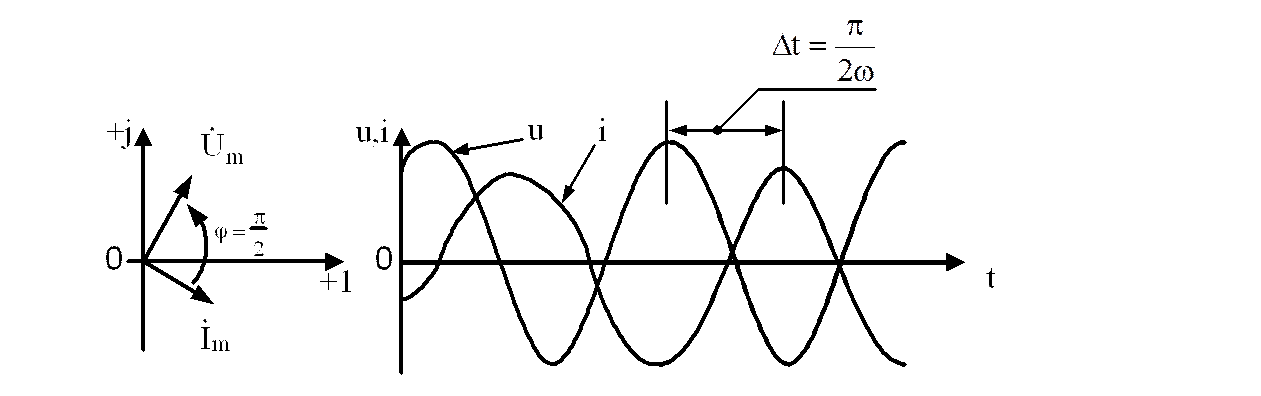 , т.е. ток в индуктивности отстает от
напряжения по фазе на
, т.е. ток в индуктивности отстает от
напряжения по фазе на ![]() (900)
(рис.1.46).
(900)
(рис.1.46).
|
||||
|
||||
Комплексное сопротивление цепи с индуктивностью
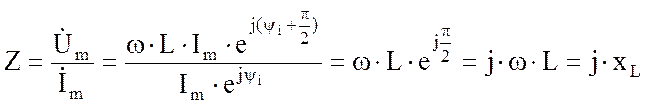
![]()
 где
где
- индуктивное сопротивление;
Индуктивное сопротивление прямо пропорционально частоте и величине индуктивности, т.е. является их линейной функцией (рис. 1.47). Графики, представляющие эту функцию, проходят через начало координат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.