Линейные цепи в установившемся режиме: Курс лекций, страница 28

На резонансной частоте имеет место    "провал"    АЧХ, т.к. при увеличении связи больше оптимальной имеет место уменьшение значе­ния АЧХ в соответствии с выражением 4.64,  как показано на рис.4.40.

Частоты f_св.1  и f_св.2 , на которых имеют место максимумы АЧХ на­-
зываются частотами связи, на этих частотах в системе возникает
второй частный резонанс, их можно вычислить из следующего условия:
второй частный резонанс имеет место при таких значения, которые определяются согласно выражению:

при А=2,41          

Из этого следует,  что при   А=2,41   разность между частотами, связи
соответствует:

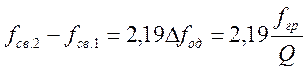                                       (4.73)

а частоты связи равны:

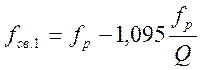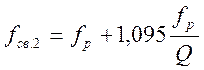  ;                                    (4.74)

При других значениях фактора связи в пределах  1 <А < 2,4 значения частот связи следует вычислять согласно выражениям:

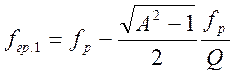       и 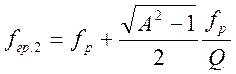                           (4.75)

а значения граничных частот согласно выражениям:

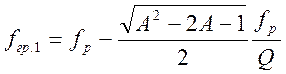              и 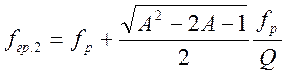                   (4.76)

На рис.4.44 пояснены причины появления двугорбости кривой
АЧХ системы связанных контуров на основе анализа зависимостей сопротивлений (собственного и вносимого) контуров от частоты.
В верхней части показаны графики собственных и вносимых активных
и реактивных сопротивлений контуров при слабой,  оптимальной и
сильной связях, а под ними - соответствующие им графики АЧХ. Как
видно из этого рисунка, при слабой связи величины вносимых сопро­тивлений   r_вн.2 и x_вн.2 значительно меньше собственных (рис.4.44а),
поэтому они заметного влияния на форму АЧХ системы не оказывают.
При увеличении модуля параметра значение общего реактивного со­противления x_общ..2 = x₂ + x_вн.2 быстро увеличивается, уменьшая тем самым, как и в одиночном конту­ре, величину напряжения U_mc2. Однако,  в системе  связанных контуров (при любой степени связи между ними),  значение U_mc2 уменьшается при этом значительно быстрее,  так как дополнительно быстро умень­шается э.д.с. E_m2, наводимая во втором контуре,  в силу увеличе­ния сопротивления первого контура:

,

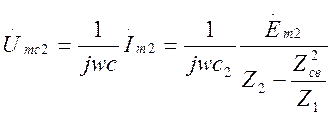где                                        ,

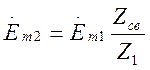Поэтому крутизна скатов АЧХ системы оказывается гораздо больше, чем у одиночных контуров, обуславливая тем самым   ее лучшие изби­рательные свойства.

При оптимальной связи в системе связанных контуров наблюдается явление - общее реактивное сопротивление   x_общ..2 = x₂ + x_вн.2 оказывается не только равным нулю при   υ=0,  но и примерно равным нулю в некотором интервале, прилегающим к этой точке (рис.4.44б),  т.е. в этом интервале частот практически существует во втором контуре явление резонанса. Поэтому величина напряжения   U_mc2 почти не меняется в этом интервале значений υ, обуславливая, тем самым, наличие плоской вершины в графике АЧХ. За пределами этого интерва­ла U_mc2 быстро уменьшается в силу рассмотренных выше причин.

Еще сильнее проявляется влияние вносимого сопротивления при
сильной связи   (рис.4_.44в). В этом случае общее реактивное сопро­тивление второго контура:

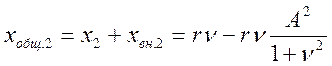
становится равным нулю при трех значениях υ:

В частности,  при υ=0 в системе возникает полный, а при

 - второй частный резонанс. Частоты, на которых воз­никает явление второго частного резонанса называются частотами связи.

Ток İm2 при полном резонансе оказывается меньшим чем при част­ных, так как вносимое активное сопротивление при  υ=0 значитель­но  больше, чем   при    

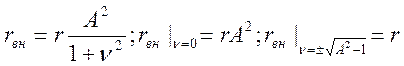
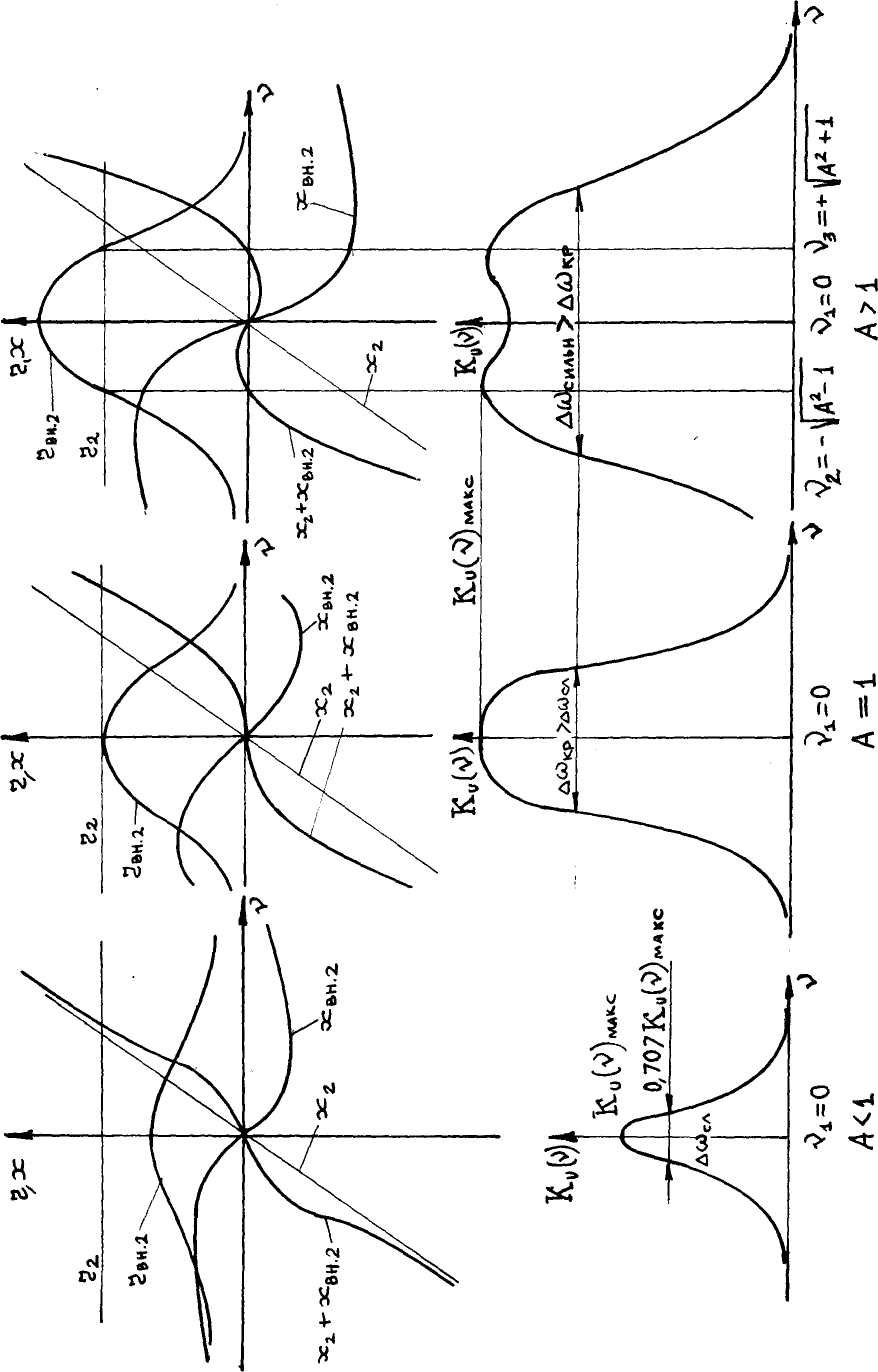
Что и вызывает явление "провала" в АЧХ. системы при сильной связи.

Анализ формы графиков АЧХ системы связанных контуров показы­вает,  что с увеличением степени связи растет и полоса пропуска­ния. Однако при очень сильной связи "провал" АЧХ опускается ниже уровня   0,707 от своего максимального значения, поэтому целесо­образно выбирать при настройке значение связи,   соответствующее А  2,41.

ВЫВОДЫ.    Система связанных колебательных контуров имеет ряд пре­имуществ перед одиночными контурами:

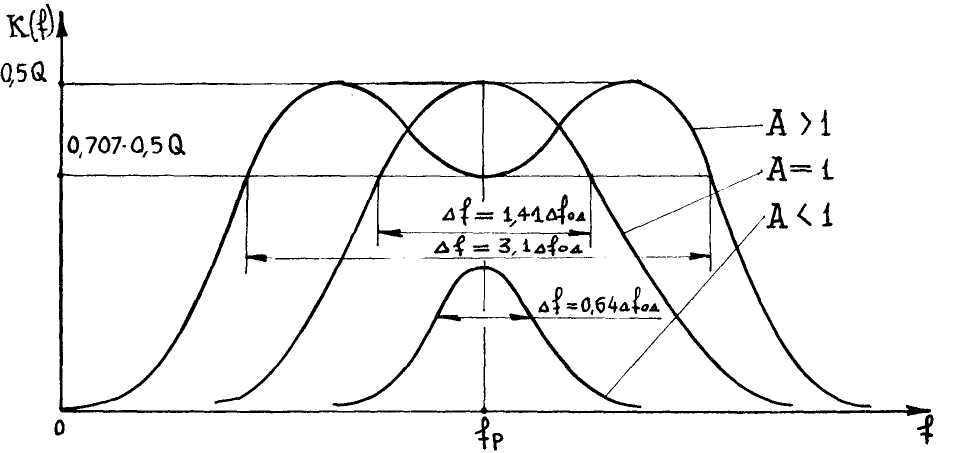Рис. 4.45

1.  Сравнивая АЧХ системы контуров при различных степенях связи (рис.4.45), можно сделать вывод о том,  что в системе связанных контуров можно существенно (примерно в 5 раз) изменять полосу про­пускания в пределах:

     без значительных изменений значений АЧХна резонансной частоте.
2. Значения АЧХодиночных контуров на частотах,  отличных от резонансной частоты убывают относительно максимального пропорциональ­но множителю:

В тоже время значения АЧХ системы связанных контуров убывают шхшорвдонально множителям:

Из сравнения можно сделать вывод,   что системы связанных кон­туров обладают более высокими избирательными свойствами,  чем оди­ночные контуры.

t

3. Система связанных контуров может быть использована с источни­ками,  обладающими либо малым, либо большим внутренним сопротивле­нием (см.рис.4.32 и 4.33)

Примеры использования связанных колебательных контуров приве­дены на рис.4.36,  4.37,  4.38. Рассмотренные  схемы иллюстрируют использование системы "последовательный контур + последовательный контур".

На рис.4.46 приведена схема, иллюстрирующая применение системы "параллельный контур + последовательный контур", во входной цепи радиоприемного устройства и между каскадами усиления радиоприем­ного устройства.

В такой схеме настройка всех идентичных контуров на заданную частоту осуществляется одновременно изменением емкостей, контуров.

Кроме систем,   состоящих из двух контуров,  нашли применение системы,  состоящие из 3-х и большего числа связанных конкуров.