Начиная со значения ![]() значения
значения ![]() – повторяются. Кроме того, в
пределах одного периода первые
– повторяются. Кроме того, в
пределах одного периода первые ![]() значений
значений ![]() отличаюся от вторых
отличаюся от вторых ![]() значений лишь знаком.
Действительно,
значений лишь знаком.
Действительно, 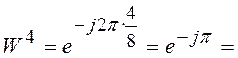
![]() ;
;  ,
и т.д.
,
и т.д.
Устранение избыточных умножений приводит к так называемому быстрому преобразованию Фурье (БПФ). Оно позволяет многократно
|

сократить число операций и обеспечивает более скоростные и эффективные вычисления коэффициентов ДПФ.
Рассмотрим один из способов построения алгоритмов БПФ, называемый способом прореживания по времени.
Пусть требуется вычислить ДПФ входной
последовательности (массива отчетов) дискретного сигнала ![]() , имеющего четное число
отсчетов, причем
, имеющего четное число
отсчетов, причем ![]() , где т –
целое число.
, где т –
целое число.
Представим входную последовательность
в виде двух предпоследовательностей с четными и нечетным номерами и половинным
числом членов в каждой последовательности (рисунок 2.15): ![]() ;
; ![]() ;
;
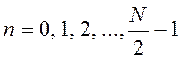 . Определим спектры этих
последовательностей с четным и нечетными номерами отдельно:
. Определим спектры этих
последовательностей с четным и нечетными номерами отдельно:
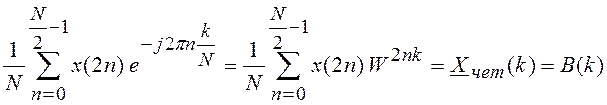 ;
;
|

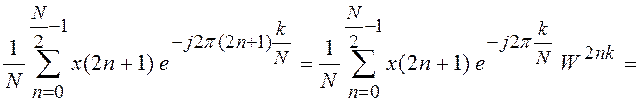
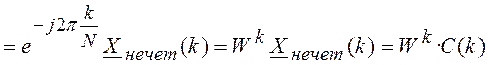 , где
, где 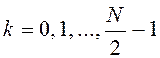 .
.
Следовательно, значения ![]() ДПФ найдется как сумма
ДПФ найдется как сумма
![]() (2.15)
(2.15)
где ![]() .
.
Таким образом, N-точечное
преобразование ![]()
![]() , можно произвести, вычислив
два
, можно произвести, вычислив
два ![]() точечных преобразования:
точечных преобразования: ![]() и
и ![]() ,
с последующим их объединением по формуле (2.15). На рисунке 2.16 показан этот
прием для
,
с последующим их объединением по формуле (2.15). На рисунке 2.16 показан этот
прием для ![]() .
.
Если учесть, что ![]() ;
; ![]() ;
;
![]() , то можно сократить число
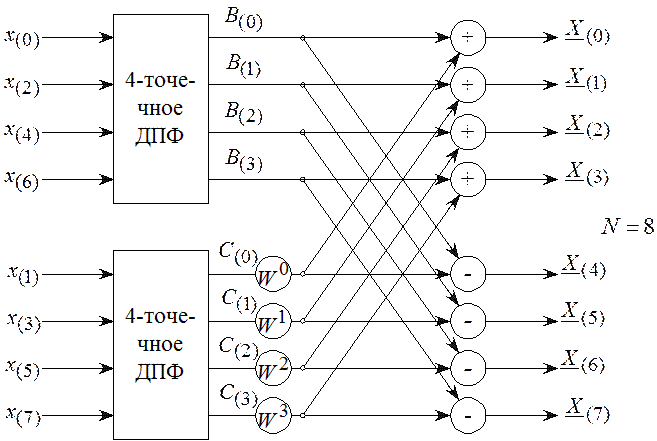
умножений вдвое. Алгоритм БПФ с учетом выше приведенных соотношений приведен на
рисунке 2.17.
, то можно сократить число
умножений вдвое. Алгоритм БПФ с учетом выше приведенных соотношений приведен на
рисунке 2.17.
|
Если ![]() в
свою очередь делить на 2, то вычисления каждого из преобразований
в
свою очередь делить на 2, то вычисления каждого из преобразований ![]() и
и ![]() можно
также свести к двум
можно
также свести к двум ![]() -точечным
преобразованием, что вызывает дополнительное уменьшение требуемого количества операций,
умножение. Такая сортировка осуществляет до тех пор, пока не образуется
-точечным
преобразованием, что вызывает дополнительное уменьшение требуемого количества операций,
умножение. Такая сортировка осуществляет до тех пор, пока не образуется ![]() последовательностей по два
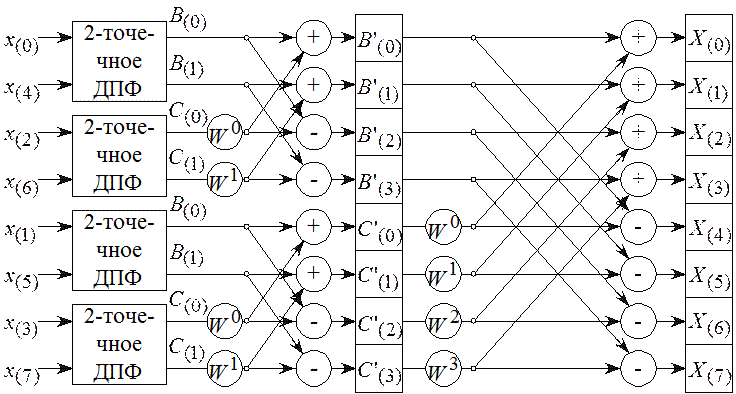
элемента в каждой. На рисунке 2.18 показано сведение 8-точечного преобразования
к четырем 2-х точечным. На рисунке 2.19 дана полная схема вычислений, в которой
дополнительно приведены вычисления, требуемые для 2-х точечных преобразований.
последовательностей по два
элемента в каждой. На рисунке 2.18 показано сведение 8-точечного преобразования
к четырем 2-х точечным. На рисунке 2.19 дана полная схема вычислений, в которой
дополнительно приведены вычисления, требуемые для 2-х точечных преобразований.
Если N представляется целой
степенью двух ![]() , то вычисления
разбиваются на
, то вычисления
разбиваются на ![]() этапов, в каждом из которых
требуется
этапов, в каждом из которых
требуется ![]() комплексных умножений. Таким
образом, количество умножений равно
комплексных умножений. Таким
образом, количество умножений равно 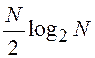 . Например,
при
. Например,
при ![]() -точечном преобразовании это чи
число умножений окажется равным
-точечном преобразовании это чи
число умножений окажется равным 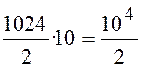 , в то
время как при
, в то
время как при
|
N-точечном ДПФ потребовалось бы ![]() операций
умножения. Как видим, БПФ обеспечивает существенное сокращение объема
вычислений (в данном примере в 200 раз).
операций
умножения. Как видим, БПФ обеспечивает существенное сокращение объема
вычислений (в данном примере в 200 раз).
Следует обратить внимание на то, что
исходные отсчеты попадают на входы преобразователя не в естественном порядке ![]() , а в порядке
, а в порядке ![]() .
.
Для получения номеров отсчетов в требуемой последовательности необходимо номера отсчетов, следующие в естественном порядке, представить в двоичной системе счисления, а затем в каждом из двоичных представлений переставить разряды, записав их в обратном, так называемом, двоично-инверсном порядке
|
десятичные номера отсчетов |
→ |
(0) |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
|
естественный порядок |
→ |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
двоично-инверсный порядок (бит-реверсия) |
→ |
000 |
100 |
010 |
110 |
001 |
101 |
011 |
111 |
|
десятичные номера |
→ |
(0) |
(4) |
(2) |
(6) |
(1) |
(5) |
(3) |
(7) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.