Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 32

Минимально-фазовые КИХ обладают нелинейной ФЧХ . Процесс интерполяции соответствует варианту 3: сохраняется модуль спектра, но не сохраняется форма сигнала.

БИХ-фильстры обладают, как правило, нелинейной ФЧХ и в случае их использования тоже сохраняется модуль спектра, но не сохраняется форма исходного сигнала (вариант 3).

9.5 Структура систем интерполяции с целочисленным коэффициентом L

Важной особенностью и достоинством использования КИХ-фильтров в системах интерполяции цифрового сигнала является то, что при высокой выходной частоте дискретизации  фильтр работает фактически на нижней входной частоте дискретизации 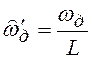. Это можно объяснить следующим образом. Если передаточная функция фильтра 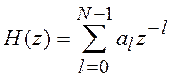 и фильтр работает на частоте дискретизации 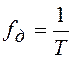, то в нем нужно выполнить N операций умножения не за интервал времени Т, а за интервал, равный интервалу дискретизации входного сигнала . Это объясняется тем, что в последовательности  на входе фильтра после ЭДЧ между каждой парой информационных отсчетов находится L – 1 нулевых отсчетов, умножать на которые естественно нет необходимости (рисунок 9.6).

Рассмотрим две структуры интерполяции.

1) Последовательная структура

Входной сигнал  поступает на ЭДЧ, осуществляющий предварительное увеличение частоты дискретизации в L раз по алгоритму (9.1), т.е. добавляющий L-1 нулевых отсчетов между каждой парой отсчетов сигнала . Выходной сигнал ЭДЧ  обрабатывается КИХ фильтром с передаточной функцией вида 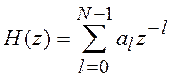, реализованным в прямой форме (порядок фильтра N). Обычно выбирается  ( – целое число). К недостаткам данной схемы можно отнести то, что на выполнение операции умножения отводится один интервал времени Т, т.е. умножители в схеме работают на “высокой” выходной частоте дискретизации .

2) Более эффективной системой интерполяции является параллельная структура с использованием КИХ-фильтра, в которой умножители работаю на “низкой” (входной) частоте дискретизации.

В этой схеме при поступлении на ее вход отсчета входного сигнала  сразу вычисляются все произведения , , которые затем используются в соответствующий момент для вычисления сигнала . Очевидно, что в этом случае умножители работают на “низкой” входной частоте дискретизации, поскольку следующий отсчет входного сигнала  поступает на вход умножителей только через интервал времени . На выходе каждого умножителя стоит ЭДЧ, добавляющий по L – 1 нулевому отсчету между каждой парой информационных отсчетов. Формирование отсчета выходного сигнала  осуществляется с помощью цепи сумматоров, соединенных между собой через элементы задержки на интервал дискретизации Т. Т.о. умножители работают на “низкой” частоте ,а цепи элементов задержки и сумматоры – на “высокой” (выходной) частоте . К недостаткам структуры 2 повышения частоты дискретизации ЦС следует отнести то, что цепь элементов задержки и сумматоров по-прежнему работает на “высокой” выходной частоте дискретизации, а также многократное возрастание количества эспандеров, линий задержки и сумматоров.

10 Уменьшение частоты дискретизации (децимация) цифрового сигнала

10.1 Общие сведения

Рассмотрим аналоговый сигнал , спектр которого  занимает полосу частот от 0 до  (рисунок 10.1,а).

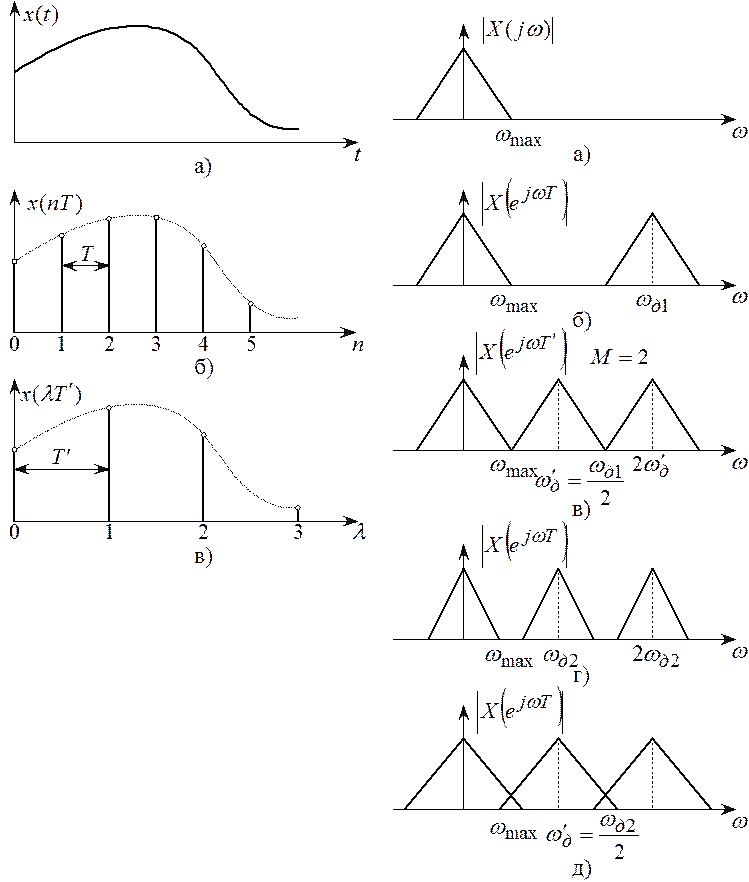
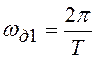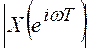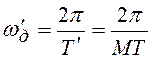Осуществим дискретизацию этого сигнала с интервалом дискретизации Т (частотой ). Соответствующий дискретный сигнал  и модуль спектра дискретного сигнала  изображена на рисунке 10.2,а 10.2,б. Теперь осуществляем дискретизацию этого же сигнала  с частотой . Соответствующий дискретный сигнал  для  изображен на рисунке 10.1,в. Рассмотрим спектр этого дискретного сигнала. Здесь возможны 2 случая.