Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 22

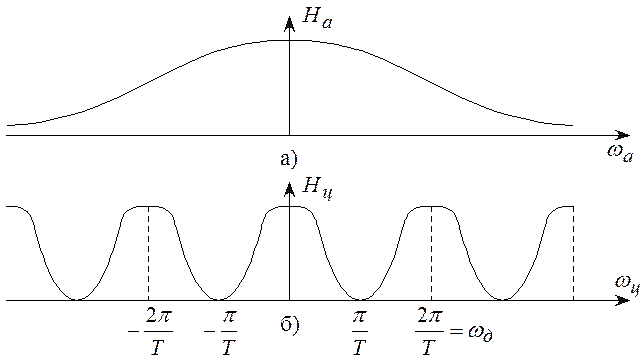
ный коэффициент передачи цифрового фильтра представляет собой периодическую функцию частоты с периодом ее повторения, определяемым частотой дискретизации . Для сравнения, на рисунке (6.7) показаны АЧХ аналогового фильтра-прототипа и цифрового фильтра, откуда следует, что они имеют идентичный вид.

Однако, характеристики ЦФ, сохраняя масштаб по оси ординат, сжимаются по оси частот в определенное число раз. Поэтому при синтезе ЦФ по методу инвариантности частотных характеристик используют условие, что весь интервал частот , относящийся к аналоговому фильтру, преобразуется в полосу частот  цифрового фильтра, удовлетворяющего неравенству:

.

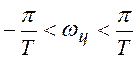Использование стандартного преобразования  или 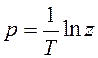 не приведет к дробно-рациональной функции, поэтому для ФНЧ применяют замену переменой вида

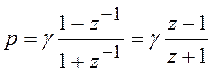,                                      (6.21)

где  – постоянный множитель, значения которого не меняет формы преобразования (о выборе  поговорим позже).

Билинейное преобразование (6.21) переводит все точки из левой полуплоскости переменной р в точки на и внутри единичной окружности плоскости Z. Так что, если была устойчивой аналоговая цепь, будет устойчивой и дискретная цепь.

Из (6.21) можно найти и обратное соотношение:

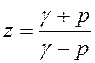.                                              (6.22)

Использование подстановки (6.21) обеспечивает однозначное преобразование передаточной функции  аналогового фильтра-прототипа в передаточную функцию  цифрового фильтра

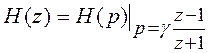
Но не все так хорошо. Так, соотношение между нормированными “аналоговыми” частотами  и нормированными “цифровыми” частотами , которые можно получить из (6.21) является нелинейным.

Поскольку 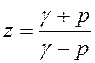, то подставляя в это выражение вместо  и вместо , получим:

.

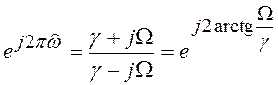Отсюда легко получить:

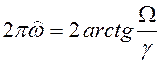
или

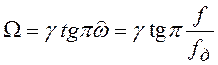.                                    (6.23)

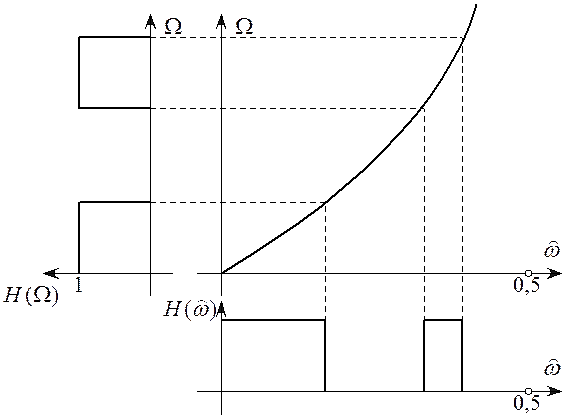
При изменении частоты  от 0 до  или  от 0 до 0,5 нормированная частота  в шкале аналоговых частот будет пробегать значения от 0 до бесконечности. Таким образом имеет место “деформация” шкалы частот. На рисунке 6.8 изображена зависимость (6.23) и проиллюстрировано явление деформации частотной шкалы. Слева показана идеализированная АЧХ аналогового полосового фильтра с двумя полосами пропускания, равными по величине, но расположенными в разных частотных диапазонах. Полученный ЦФ будет иметь также две полосы пропускания, но ширина последней в области верхних частот будет существенно меньше ширины ПП в области нижних частот.

Из рисунка видно, что в области нижних частот, где функция 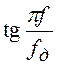 мала, частотные характеристики аналогового и цифрового фильтров почти совпадают. Далее по мере ускорения роста функции тангенса, частотная характеристика дискретного фильтра все сильнее сжимается по горизонтали (по сравнению с аналоговым прототипом), а на частоте  достигает значения, которое частотная характеристика аналогового фильтра имела бы на бесконечной частоте.

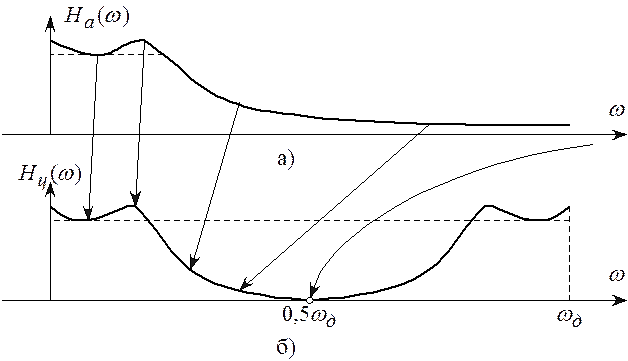
На рисунке 6.9 проиллюстрирована трансформация частотной оси при билинейном Z-преобразовании для фильтра нижних частот.

Выход, однако, чрезвычайно прост. Деформация шкалы частот не приводит к нарушению избирательных свойств при билинейном преобразовании (и это главное). А деформацию шкалы частот можно скомпенсировать с помощью предискажений в аналоговом фильтре.

Как выбрать параметр ?

Во многих справочниках по расчету аналоговых фильтров граничная частота полосы пропускания принимается равной 1: 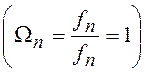. Поскольку , то, чтобы обеспечить цифровой фильтр с граничной частотой  соответствующей , необходимо  взять равным:

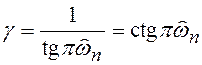; .                            (6.24)

Обобщенное билинейное преобразование