Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 21

Для того, чтобы функция  была функцией наименьшего равномерного приближения при заданных  и k необходимо и достаточно, чтобы функция  принимала наибольшие и равные друг другу по абсолютной величине и чередующиеся по знаку значения в  последовательно расположенных точках (точках

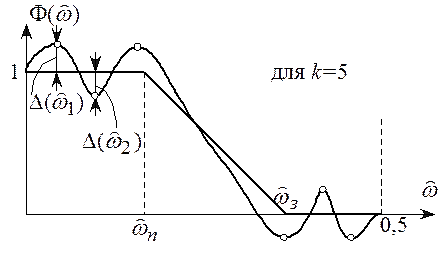
альтернанса)  интервала , например, как это показано на рисунке 6.5.

Наиболее эффективным алгоритмом построения на ЭВМ функций наилучшего равномерного приближения является алгоритм Ремеза. Суть этого алгоритма состоит в пошаговой модификации коэффициентов  до тех пор, пока не будут выполнены условия:

6.5 Синтез фильтров с бесконечной импульсной характеристикой (БИХ-фильтров)

6.5.1 Постановка задачи

Задача проектирования БИХ-фильтров является достаточно многоэтапной и сложной, причем отдельные этапы проектирования могут быть решены только с помощью ЭВМ.

Вначале нужно решить аппроксимационную задачу, т.е. определить коэффициенты  и  передаточной функции  по заданным требованиям к характеристикам фильтра. Затем следует выбрать структуру фильтра и рассчитать разрядность входного сигнала, коэффициентов передаточной функции и внутренних кодов фильтра. Теперь, имея все необходимые параметры необходимо проверить соответствие полученного фильтра поставленным перед проектированием требованиям. Этот этап можно выполнить с помощью моделирования фильтра на ЭВМ. Завершающим этапом является разработка функциональной схемы и его схемотехническая реализация.

В настоящем разделе рассмотрим начальный этап проектирования – методы определения передаточной функции. Основное внимание будет уделено избирательным фильтрам. При определении передаточных функций БИХ-фильтров используются разные методы. Наибольшее распространение получили два метода: метод инвариантности импульсных характеристик и метод билинейного преобразования.

6.5.2 Метод инвариантности импульсных характеристик

Данный метод основан на подобии (инвариантности, или неизменности) импульсной характеристики аналогового фильтра-прототипа и полученной из нее путем дискретизации импульсной характеристики ЦФ (рисунок 6.6).

Данный метод синтеза осуществляется путем применения прямого Z-преобразования к импульсной характеристике и вычислении системной функции . Для приведенного примера  представляет собой бесконечный ряд:

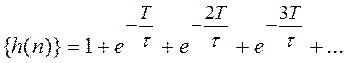
Выполнив Z-преобразование данной импульсной характеристики, получим

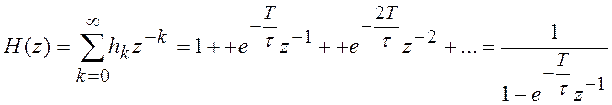.      (6.19)

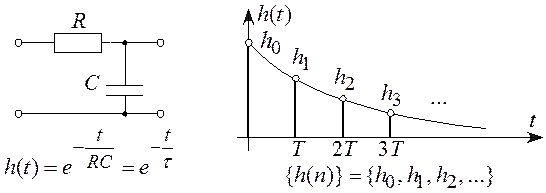
Таким образом, функция (6.19) определяет рекурсивный ЦФ 1-го порядка, содержащий масштабный блок, элемент задержки и сумматор.

Из этого соотношения путем подстановки  находим частотный коэффициент передачи цепи:

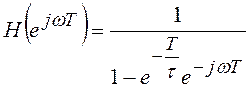.                                 (6.20)

6.5.3 Метод инвариантности частотных характеристик (метод билинейного преобразования)

Для расчета избирательных БИХ фильтров со стандартными характеристиками (ФНЧ, ФВЧ, ПФ, РФ) наиболее простым и широко используемым является метод билинейного преобразования.

С помощью этого метода передаточная функция  аналогового фильтра преобразуется в передаточную функцию  цифрового БИХ-фильтра. Достоинством данного метода является то, что передаточная функция цифрового фильтра определяется с помощью простых формул из передаточной функции аналоговых фильтров, для которых существуют подробные таблицы и справочники. Это позволяет решать аппроксимационную задачу без использования ЭВМ.

Достоинство этого метода заключается также в том, что данный метод обеспечивает построение такого БИХ-фильтра, выходной сигнал которого приближенно совпадает с выходным сигналом аналогового фильтра-прототипа при одинаковых произвольных входных сигналах.

В основах теории цифровых систем доказывается принципиальная невозможность создания физически реализуемого цифрового фильтра, частотный коэффициент передачи которого в точности повторяет частотный коэффициент передачи аналогового фильтра. Это связано с тем, что частот-