Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 28

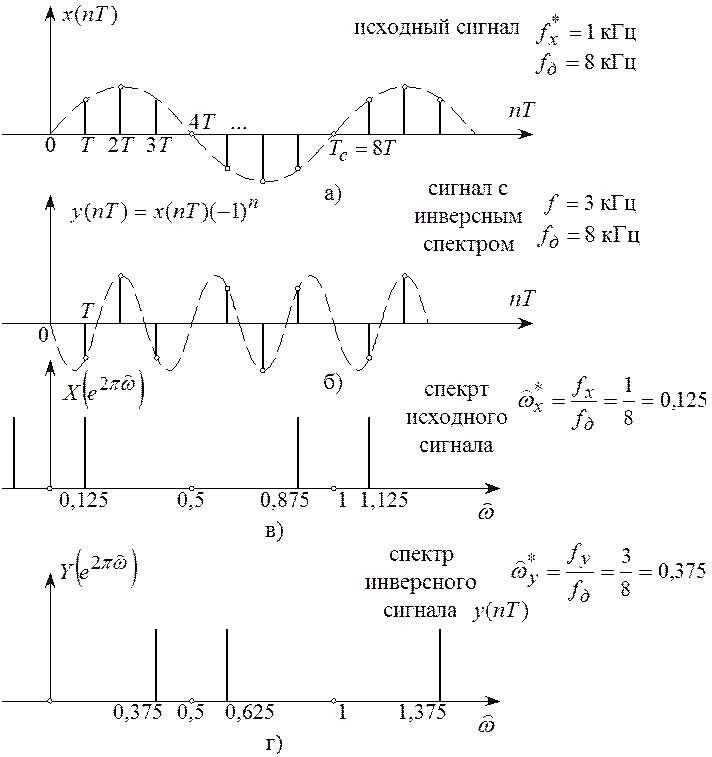
Если изменить знак каждого второго отсчета сигнала  по правилу (8.5), то получим сигнал . Из рисунка 8.4,б видно, что сигнал  есть дискретная синусоида с частотой  ( кГц), т.е. спектр  представляет собой спектр инверсного сигнала.

8.3 Формирование сигнала с ОБП

Важную роль в технике связи играют сигналы с одной боковой полосой (ОБП). Такие сигналы используются, например, при формировании многоканальных сигналов с частотным разделением каналов для получения максимального числа каналов в заданной полосе частот.

Рассмотрим дискретный вещественный сигнал , спектр которого в основной полосе нормированных частот  занимает полосу частот , причем . Модуль спектра исходного сигнала показан на рисунке 8.5,а. Задача формирования сигнала с ОБП состоит в получении такого сигнала , спектр которого содержит лишь одну боковую полосу. Модуль спектра такого сигнала показан на рисунке 8.5,д. В этом смысле спектр сигнала  содержит лишь правую боковую спектра исходного сигнала.

Т.о. задача формирования сигнала с ОБП состоит в том, что необходимо путем обработки исходного сигнала убрать (отфильтровать) одну боковую полосу спектра исходного сигнала.

Рассмотрим схему формирования сигнала с ОБП (рисунок 8.6). Исходный сигнал  умножается на дискретную экспоненту . Допустим, что 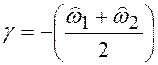 (о выборе величины  поговорим позже).

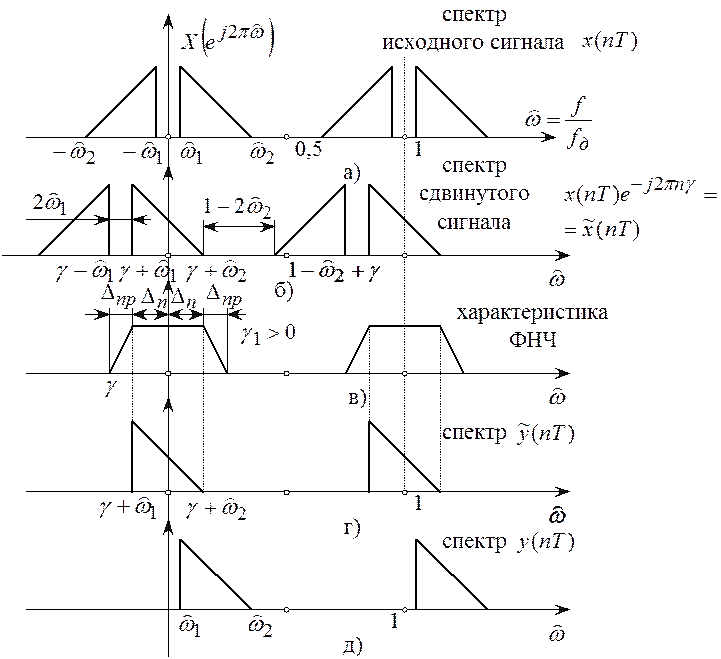
Тогда спектр исходного сигнала сдвигается влево на величину , причем верхняя боковая спектра будет располагаться симметрично, относи тельно , модуль спектра сигнала  показан на рисунке 8.5,б.

Далее правая боковая полоса выделяется ФНЧ, ширина нормированной полосы пропускания которого  равна 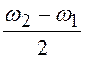, а ширина полосы неопределенности (промежуточной полосы между ПП и ПЗ) . Почему? Дело в том, что левая боковая полоса спектра исходного сигнала, которую нужно подавить с помощью фильтра, отстоит от выделяемой правой боковой полосы на величину  влево и

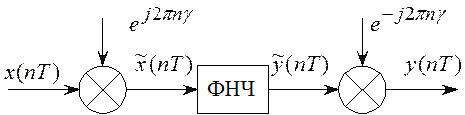
 вправо. Естественно, что  должна быть равна минимальной из них (в нашем случае ). На выходе фильтра формируется сигнал . Его спектр содержит уже ОБП, однако он расположен пока не в том же месте оси частот, в котором находилась соответствующая боковая полоса исходного сигнала. Для выполнения обратного сдвига ОБП в область частот (), сигнал  умножается на дискретную экспоненту . Модуль спектра сигнала  изображен на рисунке 8.5,д.

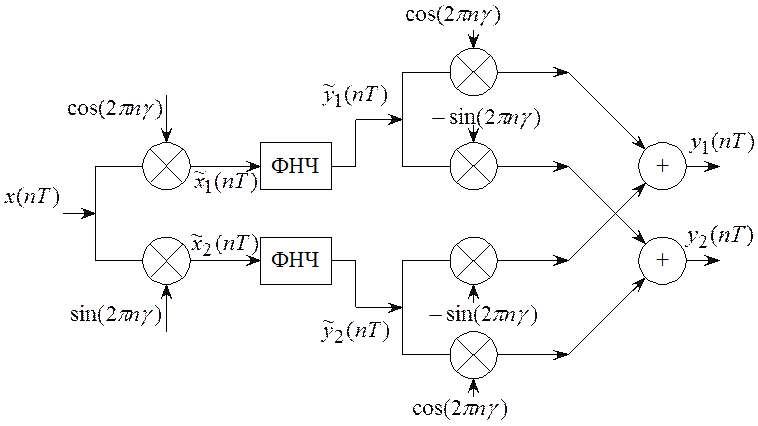
Следует помнить, что сигналы ,  и  - комплексные. Следовательно, и ФНЧ является комплексным. Это означает, что должны отдельно фильтроваться вещественная и мнимая составляющие сигнала . Более подробная схема формирования сигнала с ОБП приведена на рисунке 8.7.

В этой схеме, полностью соответствующей схеме 8.6, показана реализация операций комплексного умножения

; = ;

ФНЧ в верхней части ветви обрабатывает вещественную составляющую  сигнала , а в нижней части ветви – мнимую составляющую .

Вернемся теперь к выбору . Рассмотрим для простоты один случай:  (сдвиг спектра по оси частот влево). Коэффициент  определяет сдвиг спектра и, следовательно, параметры ФНЧ, формирующего сигнал с ОБП.

При сдвиге спектра на  левая граничная частота выделяемой полосы располагается на частоте , а правое граничное на частоте  ().

Поскольку АЧХ фильтра с вещественными коэффициентами симметрична относительно частоты  (рисунок 8.6,в), граничная частота ПП должна удовлетворять условию

.                             (8.6)

Соответственно граничная частота полосы задерживания

.                           (8.7)

из (8.6) и(8.7) видно, что в зависимости от выбранной величины  изменяются и условия, накладываемые на граничные частоты  и  фильтра, что в свою очередь скажется на сложности фильтра. Графики функций  и  изображены на рисунках 8.8,а,б для случая  и на рисунке 8.9,а,б (для случая ).