Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 16

причем возможно, что в некоторых сомножителях  некоторые коэффициенты равны нулю и, следовательно, реализуются более простой структурной схемой, чем на рисунке 5.9. Структурная схема такого вида реализации была изображена на рисунке 5.2.

Параллельная форма реализации (рисунок 5.3) соответствует представлению передаточной функции РЦФ в виде суммы

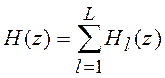,                                           (5.11)

где слагаемые 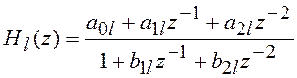 могут быть реализованы в виде упрощенных структур биквадратных блоков.

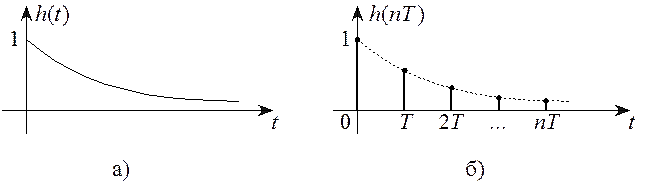
Основное достоинство рекурсивных фильтров – существенное сокращение числа элементов по сравнению с их числом в нерекурсивных фильтрах, выполняющих те же операции. Это позволяет реализовать цифровые фильтры с импульсными характеристиками, имеющими теоретически бесконечное число отсчетов. Поэтому в радиотехнике рекурсивные ЦФ получили название фильтров с бесконечными импульсными характеристиками (БИХ-фильтров). Кроме того, РФ по своим частотным свойствам гораздо ближе к аналоговому прототипу.

Пример 5.6 Рассмотрим случай, когда импульсная характеристика аналоговой цепи  (рисунок 5.9,а) аппроксимируется бесконечной дискретной последовательностью (рисунок 5.9,б) .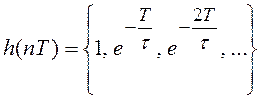

Выполнив Z-преобразование импульсной характеристики, получим системную функцию

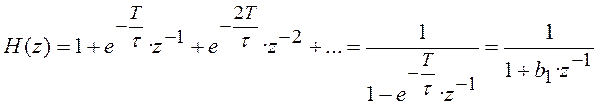, где .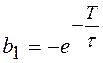

Данной системной функции соответствует нерекурсивный ЦФ с бесконечным числом элементов задержки или РЦФ первого порядка, содержащий один умножитель, один сумматор и один элемент задержки (рисунок 5.12).

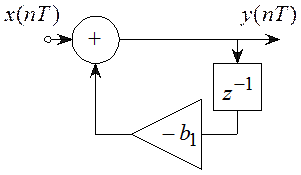
Итак, реализовать  в виде нерекурсивного ЦФ невозможно, т.к. потребуется бесконечное число элементов задержки, поэтому нерекурсивные ЦФ всегда имеют импульсную характеристику с конечным числом отсчетов (КИХ-фильтры).

Рекурсивный ЦФ может быть как КИХ фильтром, так и БИХ фильтром.

К недостаткам РЦФ следует отнести более высокие собственные шумы по сравнению с НЦФ. Кроме того, не всегда обесценивается устойчивость фильтра.

5.4 Устойчивость и реализуемость дискретных (ЦФ) фильтров

Линейный дискретный фильтр физически реализуем, если его реакция (выходной сигнал) не опережает входного сигнала, т.е. в любой момент времени  реакция  зависит лишь от значений входной последовательности  в моменты времени  и не зависит от их значений в последующие моменты.

Критерием физической реализуемости линейного ЦФ является равенство нулю всех отсчетов импульсной характеристики  при .

Дискретная цепь является устойчивой, если реакция фильтра на любое ограниченное воздействие  также ограничена, т.е. если

 для всех , то  для всех п, причем  – постоянные, не зависящие от п.

Наоборот, дискретная цепь является неустойчивой, если ограниченное по амплитуде входное воздействие вызывает на ее выходе бесконечно нарастающий отклик.

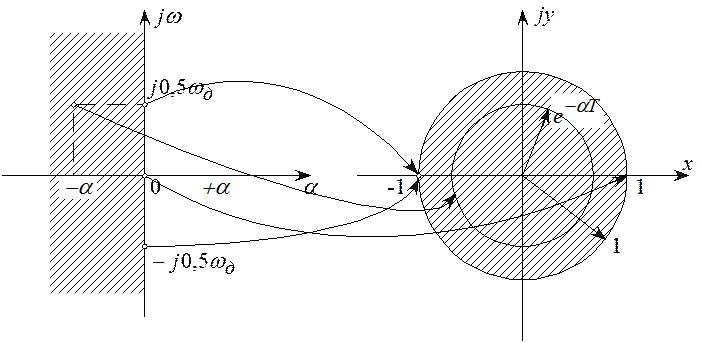
Известно, что у устойчивой аналоговой цепи полюсы передаточной функции  располагаются в левой полуплоскости комплексной плоскости р. При переходе от аналоговой цепи к дискретной и замене преобразования Лапласа Z-преобразованием точки левой полуплоскости переходят в точки, лежащие внутри единичной окружности Z-плоскости (рисунок 5.11).

Таким образом, полюсы передаточной функции  устойчивой дискретной цепи располагаются внутри единичной окружности Z-плоскости. На нули передаточной функции ограничений нет. Итак, нерекурсивный ЦФ (КИХ) фильтр устойчив всегда, т.к. знаменатель  этого фильтра равен 1.

.

Для рекурсивных ЦФ (БИХ)-фильтров  является дробно-рациональной функцией

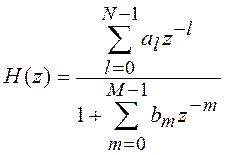
и полюсы  – это корни знаменателя

Пример 5.7 Передаточная функция РЦФ 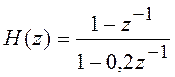. Выяснить, является ли цепь устойчивой. Полюс  – это корень знаменателя ; ; , т.е. фильтр устойчив.

Пример 5.8 Передаточная функция РЦФ равна

.

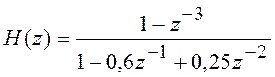Проверить фильтр на устойчивость.

; ; , т.е. фильтр устойчив.