Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 19

Реализационные критерии определяют требования к элементам аппаратурной или программной реализации фильтра: число операций сложения, умножения, число ячеек оперативной памяти и т.д.

Критерии качества обработки определяют требования к основным характеристикам фильтра (АЧХ, ФЧХ, ГВЗ, импульсной) и влияют на их качество обработки.

Рассмотрим ряд типовых требований к характеристикам фильтра, сформулированных в виде отдельных задач. Прежде всего отметим, что в большинстве приложений используются нерекурсивные ЦФ с точно линейной ФЧХ. В каждой из рассматриваемых задач под расчетом фильтра подразумевается решение аппроксимационной задачи – определение по заданным требованиям коэффициентов передаточной функции .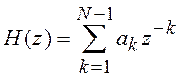

Задача 1 Фильтр должен иметь точно линейную ФЧХ (постоянное ГВЗ). Амплитудно-частотная характеристика фильтра  должна удовлетворять требованию  при условии минимума величины

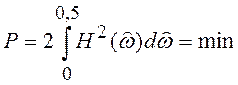                                 (6.3)

Условие (6.3) соответствует максимальному подавлению стационарного шума, поданного на вход фильтра.

Задача 2 Фильтр должен иметь точно линейную ФЧХ. АЧХ фильтра должна удовлетворять условию

, ,                           (6.4)

где  и  – заданные функции.

Критерий (5.2) называют равномерным критерием аппроксимации. Как правило, этот критерий используется при проектировании избирательных фильтров и фильтров-корректоров.

Задача 3 Мощность собственных шумов фильтра должна быть равна нулю. К ФЧХ фильтра не предъявляется каких-либо требований, а АЧХ фильтра должна удовлетворять условию:

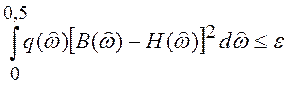,                           (6.5)

где  и  – заданные функции;

 – константа.

Критерий (6.5) называют среднеквадратичным критерием аппроксимации. Как правило, этот критерий используется при проектировании фильтров – подавителей шумов и избирательных фильтров.

Помимо задач 1-3 существует много иных задач. Задачи 1-3 сформулированы лишь для КИХ фильтров.

6.4 Проектирование нерекурсивных ЦФ

6.4.1 Синтез с использованием окон

Данный метод предназначен для синтеза нерекурсивных фильтров. Идея его очень проста. Прежде всего задается желаемый комплексный коэффициент передачи в виде непрерывной функции, определенной в диапазоне частот от  до . Так как АЧХ  цифровых фильтров является периодической функцией частоты, то ее можно представить в виде ряда Фурье:

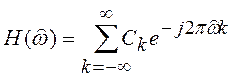                                    (6.6)

Для получения КИХ-фильтра с аппроксимирующей передаточной функцией вида

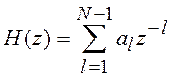
следует найти обратное преобразование Фурье для (6.6), оставив лишь конечное число слагаемых в выражении (6.6). Если у ряда выбираются максимальные по модулю коэффициенты, то результирующая частотная характеристика  будут лучшей аппроксимацией в смысле наименьших квадратов при заданном числе слагаемых.

Простое усечение последовательности отсчетов импульсной характеристики соответствует использованию прямоугольного окна. Оказывается, что такой подход не всегда приемлем. Выясним, что происходит при обрезании ряда. Введем функцию окна , равную 1 при  и 0 в остальных точках. Тогда

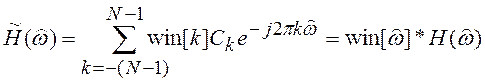, т.е.  является результатом свертки  со спектром окна . Непосредственно находим, что спектр окна

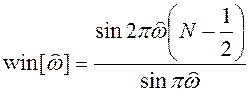                                 (6.7)

График этой функции изображен на рисунке 6.3,а.

Она напоминает -функцию и содержит боковые лепестки. В результате появляются переходные полосы между полосами пропускания и задерживания, наблюдаются колебания АЧХ в полосе пропускания, а в полосе задерживания АЧХ приобретает лепестковый характер.

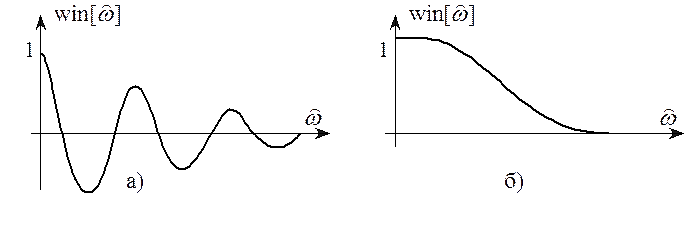
Это явление получило название явление Гиббса. Для ослабления периодических эффектов и прежде всего для уменьшения уровня лепестков в полосах задерживания вместо прямоугольных окон используют другие окна: треугольные окна, окна Хэмминга, Блэкменса, Кайзера и др. [ ], в которых функция окна плавно спадает к краям, например:

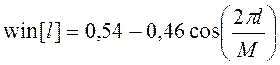,  – окно Хэмминга;        (6.8)