Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 7

Исходя из выражения (2.8) и рисунка 2.10 можно сказать, что спектральная плотность дискретного сигнала  может быть записана через известную спектральную плотность аналогового сигнала  следующим образом:

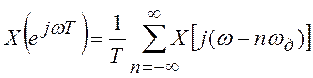                        (2.10)

Т.е. спектральная плотность дискретного сигнала представляет собой сумму бесконечного числа “копий” спектральной плотности исходного аналогового сигнала, сдвинутых относительно друг друга на частоту дискретизации .

2) При сдвиге спектра  по оси частот вправо на величину  получим спектр .

Этот спектр будет соответствовать последовательность

                                    (2.9)

3) При сдвиге дискретного сигнала  вправо, т.е. при задержке сигнала  на k интервалов дискретизации спектр задержан

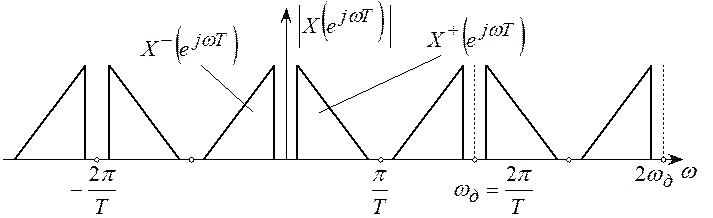
ного сигнала будет равен

                                 (2.10)

Очень важно правильно выбрать частоту дискретизации . При выполнении условий, определяемых теоремой Котельникова, операции дискретизации и восстановления сигнала взаимно обратимы. Поскольку спектр дискретизированного сигнала повторяется с частотой дискретизации, то при правильном выборе  спектры дискретизированного сигнала  не перекрывается (рисунок 2.11,б)

При неудачном выборе интервала дискретизации 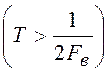 будет иметь место наложения друг на друга спектров из разных периодов повторения, т.е. искажения формы спектра и несовпадение его в диапазоне частот от  со спектром аналогового сигнала, а значит и невозможность восстановить исходный аналоговый сигнал  по дискретному  (рисунок 2.11,г).

Вывод: все наложения (сигналов или спектров) происходят из-за неудачного – слишком редкого интервала дискретизации (соответственно

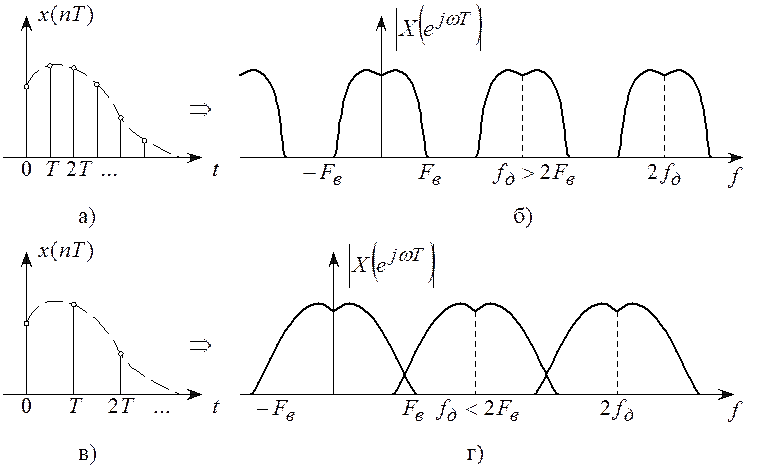
спектра или сигнала). Это приводит к появлению ошибок наложения, или, другими словами, искажений формы сигнала (либо спектра) на каждом периоде.

К примеру, спектр телефонного сигнала составляет 0,3÷3,4 кГц. Какой должна быть частота дискретизации? Согласно теореме Котельникова  кГц. Реально выбрана величина  кГц ( мсек.).

Как восстановить непрерывный сигнал из дискретного? Поскольку спектр дискретного сигнала содержит (в самом первом периоде) спектр исходного аналогового сигнала, то, пропустив дискретный сигнал  через идеальный фильтр нижних частот с граничной частотой  и с АЧХ  в полосе пропускания, выделим спектр, соответствующий исходному аналоговому сигналу . Такой фильтр подавит все “боковые” спектры и не внесет никаких изменений в основной спектр.

2.3 Дискретное преобразование Фурье

Мы уже отмечали, что развитие вычислительной техники привело к появлению цифровых систем обработки сигнала. При этом, как сигнал, так и его спектр необходимо перед вводом в вычислительное устройство представить в виде отсчетов, т.е. чисел. В настоящее время обработка сигналов чаще всего производится в частотной области, что диктуется значительным сокращением объема цифровой аппаратуры и времени обработки. Как же представить спектр сигнала в виде отсчетов?

Пусть дискретной обработке подвергается аналоговый сигнал , имеющий спектр  и длительность  (рисунок 2.13,а).

Подвергнем этот сигнал дискретизации, т.е. заменим его отсчетами , взятых в момент времени . Полное этого число отсчетов сигнала равно 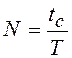, где 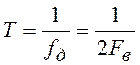 – интервал дискретизации.

Спектр дискретного сигнала станет периодическим с периодом повторения  (рисунок 2.13,б).

Мысленно продолжим дискретный сигнал периодом равным длительности сигнала . Поскольку дискретный сигнал стал периодичным, то его спектр станет дискретным (рисунок 2.13,в) с частотой дискретизации спектра 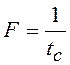. Используя преобразования Фурье для периодического сигнала, найдем комплексные амплитуды соответствующих коэффициентов

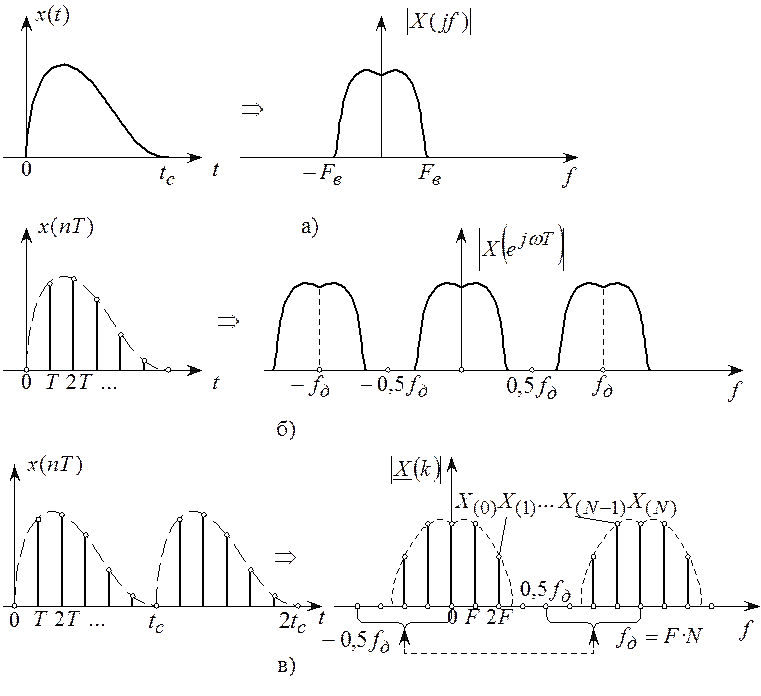
этого ряда:

,

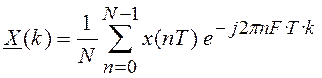так как 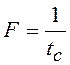, а 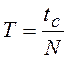, то произведение  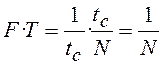и окончательно получим

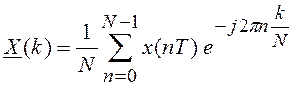,              (2.11)