Пример 5.9 Передаточная функция РЦФ равна
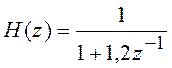 .
.
![]() ;
; ![]() ;
;
![]() – фильтр неустойчив.
– фильтр неустойчив.
Вывод: полюсы передаточной функции устойчивой дискретной цепи лежат внутри единичной окружности Z-плоскости. Нерекурсивные ЦФ всегда устойчивы.
Так, для фильтра из примера 5.4
получили, что при ![]() – (невозрастающая
функция) отклик цепи
– (невозрастающая
функция) отклик цепи
![]()
является также невозрастающей функцией, т.е. отклик ограничен. Таким образом, фильтр является устойчивым.
Одним из важных показателей ЦФ является комплексный частотный коэффициент передачи
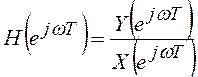 .
(5.11)
.
(5.11)
Если учесть, что 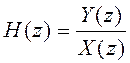 – системная функция ЦФ, то для
получения
– системная функция ЦФ, то для
получения ![]() достаточно в выражении для
достаточно в выражении для ![]() заменить z на
заменить z на ![]() , т.е.
, т.е.
 (5.12)
(5.12)
Для нерекурсивных ЦФ:
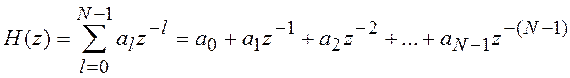 .
.
Тогда ![]() .
.
Поскольку все частотные характеристики
зависят при постоянном Т от произведения ![]() , то вместо
, то вместо ![]() можно ввести новую переменную
– нормированную частоту. Как правило, используют два способа нормирования
частоты. При первом способе полагают
можно ввести новую переменную
– нормированную частоту. Как правило, используют два способа нормирования
частоты. При первом способе полагают 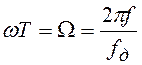 .
.
В этом случае период всех частотных
характеристик равен ![]() и требования к ним
следует задавать на интервале
и требования к ним
следует задавать на интервале ![]() . При втором
способе полагают
. При втором
способе полагают ![]() , где
, где 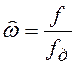 . В этом случае период
дискретизации равен
. В этом случае период
дискретизации равен ![]() и требования следует
задавать на интервале
и требования следует
задавать на интервале ![]() .
.
Будем считать, что нормированной
частотой является частота 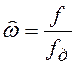 .
.
Тогда ![]()
![]()
![]() .
(5.13)
.
(5.13)
Из (5.13) легко получить АЧХ и ФЧХ цифрового фильтра
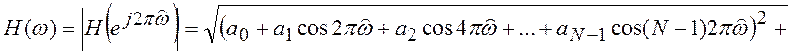
![]() .
(5.14)
.
(5.14)
Для рекурсивного ЦФ 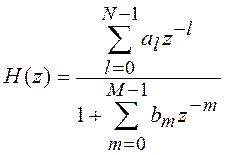 , поэтому
, поэтому
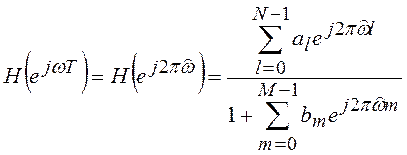 (5.15)
(5.15)
Из выражений (5.13) и (5.15) следует ряд важных свойств:
- все частотные характеристики ЦФ являются непрерывными функциями частоты;
-
все частотные характеристики являются
непериодическими функциями частоты f с периодом
повторения частоты дискретизации 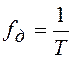 (или 1 в
масштабе нормированных частот
(или 1 в
масштабе нормированных частот ![]() ), поскольку
в выражении для
), поскольку
в выражении для ![]() входит
периодическая функция
входит
периодическая функция ![]() ;
;
- АЧХ есть четная функция от частоты, ФЧХ – нечетная функция частоты
|
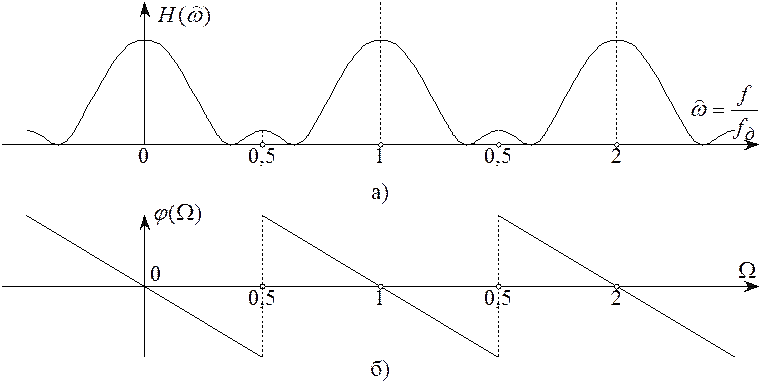
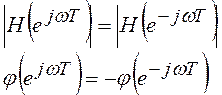 .
.
Из этих свойств следует, что требования
к частотным характеристикам следует задавать лишь на интервале в половину
периода, т.е. ![]() . На рисунке 5.14
приведен возможный вид АЧХ и ФЧХ дискретной цепи.
. На рисунке 5.14
приведен возможный вид АЧХ и ФЧХ дискретной цепи.
Пример 5.10 Найти амплитудно-частотную характеристику ЦФ с импульсной
характеристикой ![]() .
.
Запишем
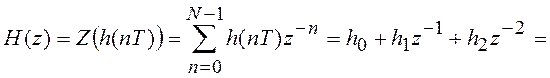
![]() – передаточная
функция нерекурсивного ЦФ.
– передаточная
функция нерекурсивного ЦФ.
Тогда
АЧХ этого фильтра равна ![]()
![]()
![]() . (5.16)
. (5.16)
Задаваясь различными значениями
нормированной частоты ![]() в диапазоне
в диапазоне ![]() получим АХЧ, график которой
приведен на рисунке 5.15.
получим АХЧ, график которой
приведен на рисунке 5.15.
|
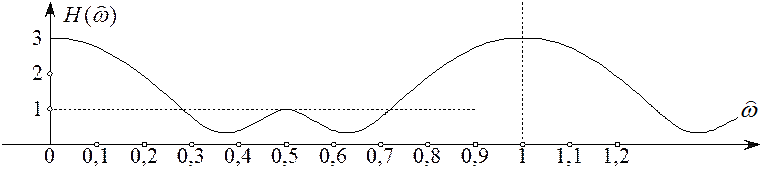

|
Из этого
рисунка видно, что ЦФ реализует в диапазоне частот ![]() частотную
характеристику фильтра нижних частот.
частотную
характеристику фильтра нижних частот.
Пример 5.11 Изменим коэффициенты усиления ![]() в
предыдущем примере на
в
предыдущем примере на ![]() ;
; ![]() . Вновь найдем выражения
. Вновь найдем выражения ![]() и построим график его АЧХ. Для
этого заменим в выражении
и построим график его АЧХ. Для
этого заменим в выражении ![]() из
предыдущего примера на коэффициенты
из
предыдущего примера на коэффициенты ![]() на новые.
Получим
на новые.
Получим
![]() .
.
Данный фильтр реализует АЧХ, соответствующую фильтру верхних частот.
Сопоставляя результаты расчетов и
графики, приведенные в примерах 5.10 5.11, можно сделать важный вывод: ЦФ легко
перестраивать. Для получения фильтров нового функционального назначения
достаточно изменить коэффициенты усиления ![]() и
и
![]() .
.
Существуют ли типовые звенья дискретной цепи? Да, сущствуют. В литературе типовыми звеньями дискретной цепи считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры (канонической схемы), если оставить в ней один или два элемента задержки.
Типовое звено первого порядка (рисунок 5.17) с передаточной функцией
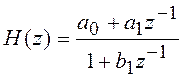
имеет АЧХ, равную
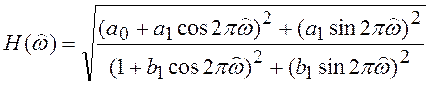 .
.
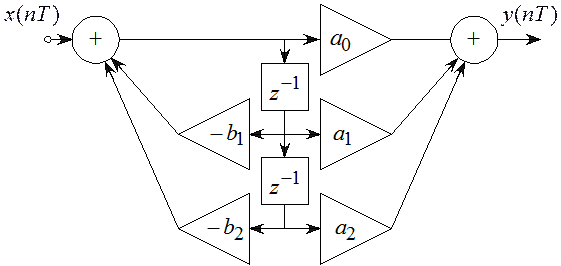
Типовое звено 2-го порядка имеет вид (рисунок 5.16) имеет передаточную функцию
|
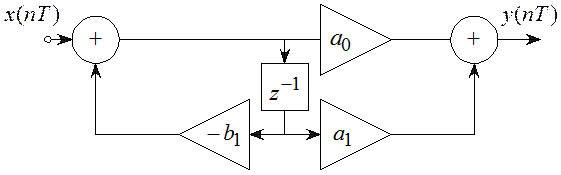
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.