Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 10

Рисунок 2.19

Убеждаемся, что полученная последовательность входных отсчетов, соответствует приведенной на рисунке 2.18.

Полученный алгоритм (рисунок 2.18) называется сигнальным графом БПФ для  отсчетов, на жагроне – “бабочка”, так как граф напоминает крылья бабочки.

Кроме алгоритма БПФ с прореживанием по времени существует алгоритм прореживания по частоте.

Замечание: Алгоритм БПФ является рекурсивным: невозможно рассчитать -точечное преобразование ДПФ, не рассчитав предварительно -точечное преобразование ДПФ.

3 Z-преобразование дискретного сигнала

3.1 Прямое Z-преобразование

Для аналоговых сигналов  известно преобразование Лапласа, позволяющее упростить вычисления. Для дискретных сигналов  используются подобное преобразование, называемое Z-преобразованием. Как известно, дискретный сигнал и его спектр описываются соотношениями

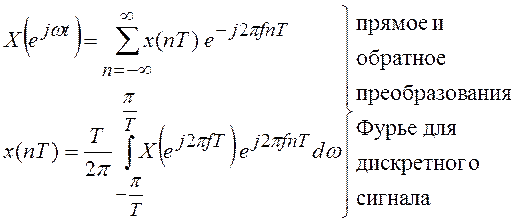
Произведем в первой формуле замену:

                                          (3.1)

Тогда формула прямого преобразования Фурье дискретного сигнала примет вид:

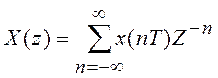                                  (3.2)

Выражение (3.2) получило название Z-преобразование или Z-изображение дискретного сигнала . Если считать, что  для , то получим одностороннее Z-преобразование:

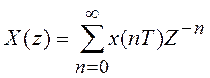.                                  (3.3)

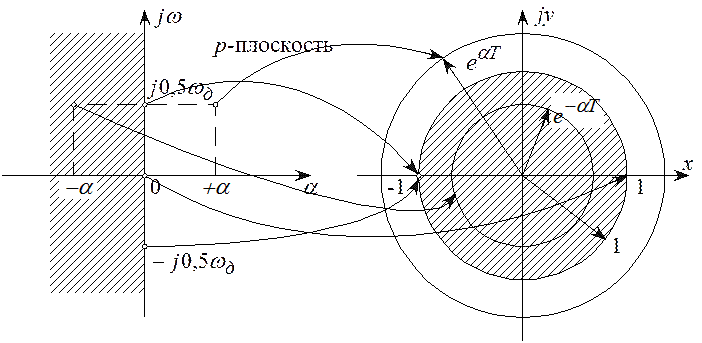
Можно указать на связь Z-преобразования с преобразованием Лапласа

,

Рисунок 3.1

 

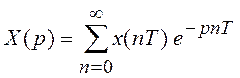которое получается путем замены . Очевидно, что  или 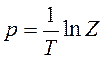. Эти формулы устанавливают связь между точками в плоскостях  и .

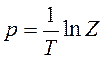Действительно, для  , т.к. ; для  .

Если положить , то мы будем перемещаться по оси  в плоскости р. При переходе в Z-плоскость точки мнимой оси  будут располагаться на единичной окружности . Причем точка  на плоскости р переходит в точку +1 на плоскости Z, а точки  в точку . Это означает, что точку отрезка  р-плоскости проецируются в точки на единичной окружности Z-плоскости.

Так как функция  – периодична, то последующие отрезки на оси  плоскости р такой же длины вновь будут проецироваться на единичную окружность плоскости Z.

Точки левой полуплоскости  соответствуют точкам внутри единичной окружности Z, а точки правой полуплоскости  – точкам вне этой окружности.

Пример 3.1 Рассмотрим Z-преобразование дискретного сигнала

.

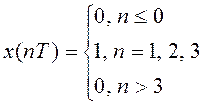Воспользовавшись формулой (3.3), получим:

.

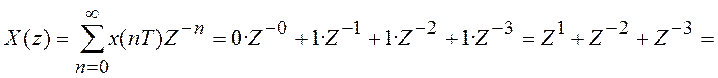
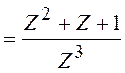Пример 3.2 Найдем Z-преобразование  дискретного экспоненциального сигнала .

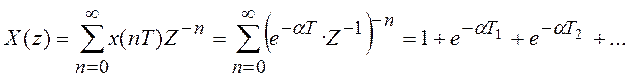
Из теории рядов известно, что при выполнении условия  ряд сходится и сумма ряда  равна 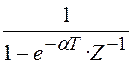, или .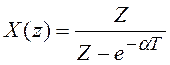

Z-преобразование  дискретного сигнала  определено точно для области Z, в которой степенной ряд (3.2) сходится. Эта область сходимости включает в себя все значения Z, находящиеся вне некоторого круга на комплексной плоскости Z, радиус которого  называют радиусом

Рисунок 3.2

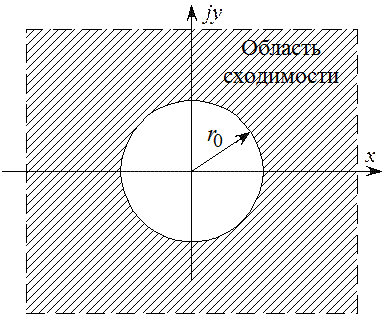
сходимости (рисунок 3.2), т.е. при  ряд сходится. В области сходимости существует взаимно-однозначное соответствие между  и , т.е. каждому  соответствует только одно , определенные для  и наоборот.

Пример 3.3 Определим радиус сходимости для Z-преобразования сигнала, заданного в примере 3.2.

Как уже было установлено, Z-преобразование сигнала  имеет вид

.

Нуль функции  будет в точке , полюс в точке , следовательно, радиус сходимости , а функция  сходится при . Окружность радиуса  приведена на рисунке 3.1. Область сходимости находится за пределами этой окружности.

3.2 Обратное Z-преобразование

Как найти дискретный сигнал по его Z-преобразованию? Для этого можно воспользоваться обратным Z-преобразованием, подобно тому, как мы пользуемся обратным преобразованием Лапласа.

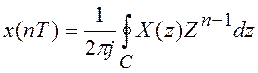,                                  (3.4)

где интегрирование вернется по замкнутому контуру С в Z-плоскости.

Другой способ заключается в том, чтобы разложить функцию  в степенной ряд по степеням . Тогда коэффициенты при степени  будут в соответствии с формулой (3.3) определять отсчеты дискретного сигнала.