Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 14

Рисунок 5.1

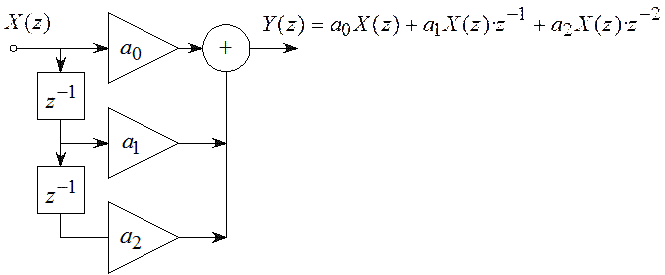
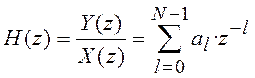                                     (5.3)

Устройство, реализующее ЦФ, выполняет последовательное умножение входной выборки сигнала на коэффициенты фильтра  и сложение полученных произведений. Структурная схема нерекурсивного ЦФ 2-го порядка (так называемого биквадратного блока – ББ) показана на рисунке 5.1 (порядком цифрового фильтра называется количество элементов задержки в схеме фильтра).

ЦФ более высоких порядков можно реализовать несколькими способами. Наиболее простым способом является так называемая прямая форма реализации ЦФ. В прямой форме ЦФ реализуется в соответствие с формулами (5.1) и (5.2). Структурная схема ЦФ в этом случае аналогична схеме, показанной на рисунке 5.1, но имеет большее число элементов задержки и умножителей.

Другим способом реализации ЦФ является каскадная (или последовательная) и параллельная формы реализации. При реализации в каскадной форме ЦФ представляется в виде последовательности следующих друг за другом звеньев ЦФ 1-го или 2-го порядка. В этом случае ЦФ реализуется в соответствии с формулой (рисунок 5.2):

.

Рисунок 5.2

 

Рисунок 5.3

 

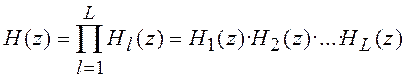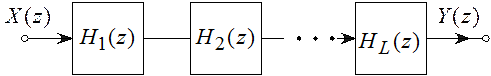
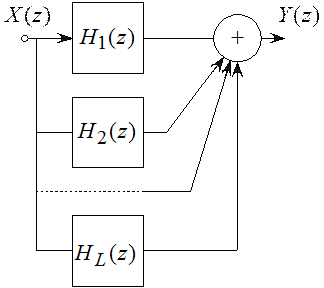
При параллельной форме реализации входная последовательность во всех звеньях одна и та же, а выходная последовательность системы равна сумме выходных последовательностей отдельных звеньев (рисунок 5.3).

Передаточная функция ЦФ рассматривается как

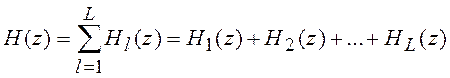
Пример 5.1 Найти передаточную функцию и структурную схему ЦФ, импульсная характеристика которого задана отсчетами:

.

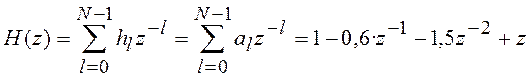, т.е. , .

Выходная последовательность в соответствие с уравнением (5.1) равна

Т.о. отсчеты импульсной характеристики  есть коэффициенты усиления фильтра . Структурная схема ЦФ, реализо-

Рисунок 5.4

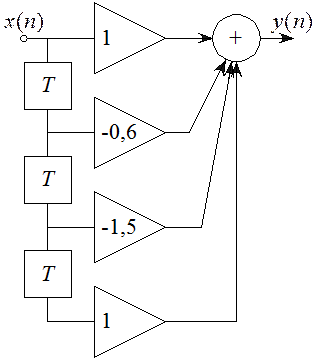
ванная в прямой форме, изображена на рисунке 5.4.

Пример 5.2 Найдем отсчеты выходного сигнала нерекурсивного ЦФ, имеющего структурную схему, рассмотренную выше, при воздействии на него дискретного сигнала .

Отсчеты выходного сигнала согласно (5.1) равны:

 (т.к. при  все отсчеты );

;

.

Аналогичным образом можно рассчитать  . Все остальные отсчеты также будут равны 0. Т.о. выходная последовательность

Графики  и  приведены на рисунке 5.5.

Рисунок 5.5

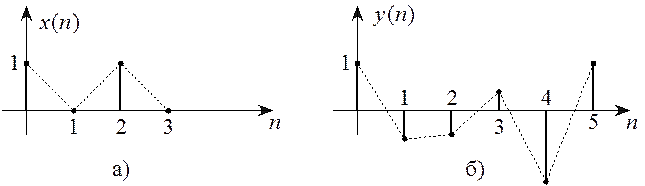
Нерекурсивный ЦФ может быть практически осуществлен, если заданная импульсная характеристика содержит ограниченное число отсчетов (КИХ-фильтр). Для получения же импульсной характеристики с большим числом членов требуется много ячеек памяти. Вместе с тем, нерекурсивные ЦФ имеют целый ряд важнейших достоинств. Они всегда устойчивы, позволяют строить фильтры с точно-линейной фазо-частотной характеристикой и манимально-фазовые фильтры, а также отличаются малыми собственными шумами и простотой настройки.

5.3 Рекурсивные цифровые фильтры (фильтры с бесконечным числом отсчетов импульсной характеристики)

Возможности нерекурсивного ЦФ существенно расширяются при введении в его схему обратных связей. Принцип работы рекурсивных ЦФ закулючается в следующем. Каждый последующий отсчет в выходном сигнале, формируемом фильтром, рассчитывается как взвешенная сумма  предыдущих рассчитанных отсчетов в выходном сигнале и  предшествующих отсчетов входного сигнала. Алгоритм работы рекурсивного ЦФ записывается в виде разностного уравнения

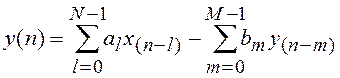                            (5.4)

Если бы не погрешность представления чисел в ЭВМ, такой фильтр имел бы бесконечное количество затухающих по амплитуде выходных отсчетов при одном единственном входном отсчете, т.е. фильтр имел бы бесконечную импульсную характеристику (БИХ-фильтр). На практике размер импульсной характеристики определяется точностью представления чисел.