Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 11

Пример 3.4 Найдем дискретный сигнал , которому соответствует Z-преобразование:

.

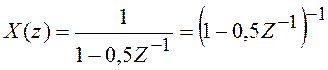Воспользуемся разложением функции  в ряд: … Для заданного Z-преобразования , поэтому запишем Z-преобразвание в виде:  +…

Сравнивая полученное изображение с общей формулой Z-преобразования 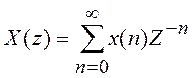 записываем последовательность

Общий член этой последовательности , .

Удобный способ вычисления Z-преобразования заключается в разложении  на простые дроби (если  – дробно-рациональная функция)

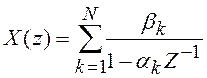                                          (3.5)

В этом случае, используя свойство линейности Z-преобразовани и условие 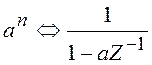, находим

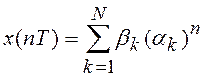.                                         (3.6)

Пусть, например, 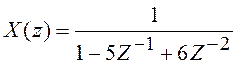. Разложим  на простые дроби:

.

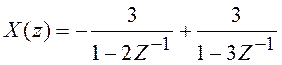Согласно (3.5) и (3.6) значения  будет равны

.

Наиболее часто используемые Z-преобразования приведены в таблице 3.1

Таблица 3.1

,
	1

3.3 Свойства Z-преобразования

Так же, как и для преобразований Лапласа и Фурье, существуют теоремы для Z-преобразования. Приведем наиболее важные.

1. Теорема линейности (суперпозиции).

Сумме дискретных сигналов соответствует сумма их изображений:

если , , то , где а и b – const.

2. Теорема задержки

Если дискретный сигнал задержан на N отсчетов, то его Z-преобразование имеет вид

                              (3.7)

3. Теорема умножения на

4. Теорема умножения на п:

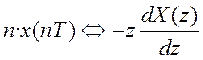
5. Теорема свертки

Свертке дискретных сигналов  и  соответствует произведение их Z-преобразований:

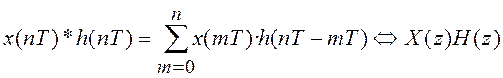           (3.8)

4 Алгоритмы и структурные схемы дискретных систем

4.1 Теорема дискретной свертки

Известно, что сигнал на выходе аналоговой цепи связан с сигналом на входе цепи интегралом наложения (интегралом свертки):

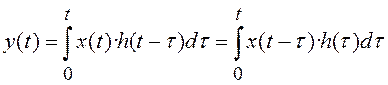,                      (4.1)

где  – импульсная характеристика цепи.

При переходе к дискретным сигналам используется выражение для дискретной свертки.

Чтобы не вносить путаницы, время t заменим дискретным значением , а время  дискретным значением . Вместо непрерывного сигнала  мы будем иметь дело с дискретным сигналом , вместо непрерывной импульсной характеристики  – с дискретной импульсной характеристикой . Тогда интеграл (4.1) запишется в виде:

.

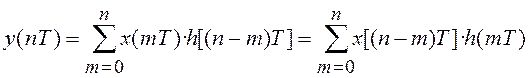Обозначая в этом выражении , , , окончательно получим, что п-ный отсчет дискретной выходной последовательности рассчитывается как

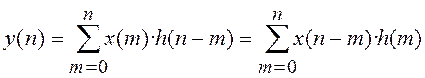.                  (4.2)

Рисунок 4.1

 

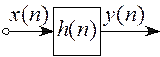
Поскольку любой отсчет сигнала – это число, то формулу (4.2) можно запрограммировать на ЭВМ. Остается лишь ввести в ЭВМ числа, соответствующие всем дискретным значениям отсчетов входного сигнала  и дискретным значениям отсчетов импульсной характеристики  и она вычислит отсчеты выходного сигнала . Выражение (4.2) на языке вычислительной техники называется алгоритмом вычисления выходного сигнала.

Пример 4.1 Рассчитаем значение выходной последовательности  цепи, имеющей дискретную импульсную характеристику , если входная последовательность имеет вид: .

Графики  и  приведены на рисунке 4.1. Пользуясь формулой (4.2), рассчитаем значения выходной последовательности .

;

;

;

;

;

;

;

;

Рисунок 4.1

Рисунок 4.2

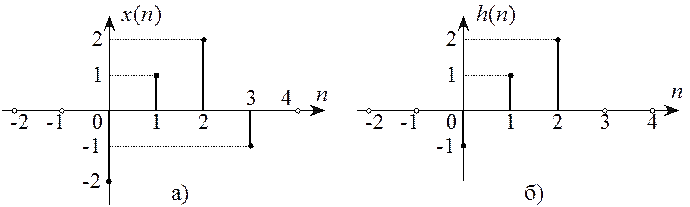
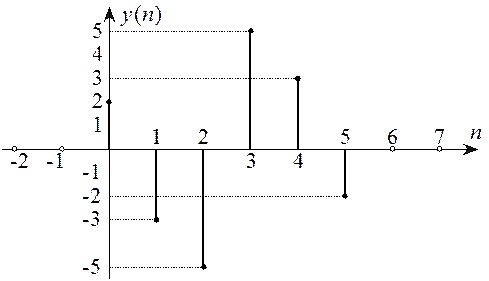
Очевидно, что  имеет длину , где  – длина последовательности входного сигнала ;  – длина последовательности импульсной характеристики .

Для нашего случая , т.е.

.

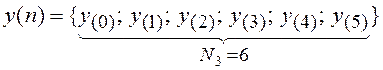График дискретного сигнала  приведен на рисунке (4.2)

4.2 Структурные схемы дискретных систем

Анализ формулы (4.2) показывает, что в ней выполняется три действия: умножение, сложение и задержка. Эти действия можно представить в виде элементов структурной схемы (рисунок 4.3).