|
|
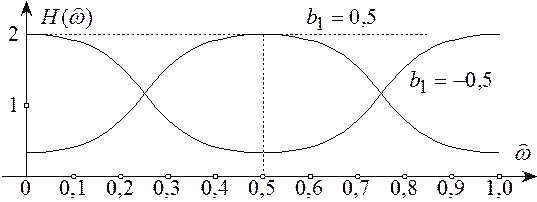
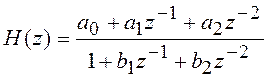 .
.
Пример 5.13 Построить график АЧХ звена 1-го порядка, у которого ![]() .
.
Передаточная функция такого звена 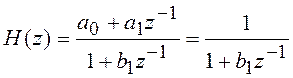 . Чтобы цепь была устойчивой
необходимо выполнить условие
. Чтобы цепь была устойчивой
необходимо выполнить условие ![]() .
.
На рисунке 5.19 построены графики АЧХ
для ![]() .
.
Т.о. при 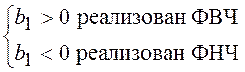 .
.
Отсюда видно, что достаточно заменить
на противоположные знаки нечетных коэффициентов знаменателя передаточной
функции фильтра ![]() и фильтр из фильтра
нижних частот превращается в фильтр верхних частот.
и фильтр из фильтра
нижних частот превращается в фильтр верхних частот.
Под проектированием (или синтезом)
цифрового фильтра понимают выбор таких наборов коэффициентов передаточной
функции ![]() и
и ![]() при
которых характеристики получающегося фильтра удовлетворяют заданным
требованиям. В задачу проектирования входит также выбор подходящей структуры
фильтра с учетом конечной точности вычислений. Это особенно актуально при
реализации фильтров в “железе” – с использованием специальных БИС или цифровых
сигнальных процессоров – DSP. Эффекты, связанные с
конечной точностью вычислений, будут обсуждаться в главе 7, здесь же пойдет
речь только о методах синтеза цифровых фильтров, т.е. способах получения
значений коэффициентов
при
которых характеристики получающегося фильтра удовлетворяют заданным
требованиям. В задачу проектирования входит также выбор подходящей структуры
фильтра с учетом конечной точности вычислений. Это особенно актуально при
реализации фильтров в “железе” – с использованием специальных БИС или цифровых
сигнальных процессоров – DSP. Эффекты, связанные с
конечной точностью вычислений, будут обсуждаться в главе 7, здесь же пойдет
речь только о методах синтеза цифровых фильтров, т.е. способах получения
значений коэффициентов ![]() и
и ![]() .
.
Методы синтеза ЦФ можно классифицировать по разным признакам:
1) по типу получаемого фильтра:
- методы синтеза нерекурсивных фильтров;
- методы синтеза рекурсивных фильтров;
2) по наличию аналогового прототипа:
- методы синтеза с использованием аналогового прототипа;
- прямые (без использования аналогового прототипа) методы синтеза.
Требования к АЧХ. Дискретная цепь может осуществлять любые операции: частотную фильтрацию сигналов, корректирование характеристики, дифференцирование сигнала и т.д., т.е. выполнять функции любой аналоговой цепи. При проектировании частотно-избирательных фильтров требования задаются к АЧХ фильтров.
Так для идеального фильтра нижних частот АЧХ фильтра имеет вид, приведенный на рисунке 6.1,а.
Очевидно, что невозможно реализовать
дискретный фильтр, АЧХ которого точно равна функции ![]() .
Поэтому необходимо аппроксимировать заданную функцию
.
Поэтому необходимо аппроксимировать заданную функцию ![]() , т.е. определить параметры
дискретного фильтра, АЧХ которого
, т.е. определить параметры
дискретного фильтра, АЧХ которого ![]() в том или
ином смысле была бы близка к заданной (рисунок 6.1,б):
в том или
ином смысле была бы близка к заданной (рисунок 6.1,б):
![]() при
при ![]() , здесь
, здесь ![]() и
и ![]() – допустимые неравномерности
АЧХ в полосе пропускания и в полосе задерживания соответственно;
– допустимые неравномерности
АЧХ в полосе пропускания и в полосе задерживания соответственно;
![]() – нормированные граничные
частоты полосы пропускания и полосы задерживания фильтра.
– нормированные граничные
частоты полосы пропускания и полосы задерживания фильтра.
Для фильтров других типов (ВЧ, полосового и режекторного) задание требований к АЧХ приведены на рисунке 6.2.
Полосы пропускания и задерживания разделены переходной полосой, в которой поведение АЧХ не нормируется.
На практике, как правило, вместо ![]() и
и ![]() задаются
логарифмические величины
задаются
логарифмические величины ![]() и
и ![]() , заданные в децибелах:
, заданные в децибелах:
|

|

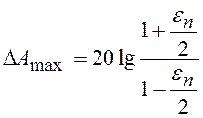 ,
(6.1)
,
(6.1)
![]() , или
, или
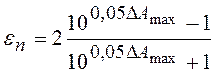 ,
(6.2)
,
(6.2)
![]() .
.
Требования к ФЧХ фильтров. Во многих случаях формулируются требования к ФЧХ цифровых фильтров.
Фильтры с точно-линейной ФЧХ имеют постоянное групповое время замедления (ГВЗ) 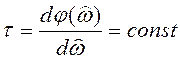 и не искажают форму сигнала,
спектр которого находится в полосе пропускания. КИХ-фильтры при определенных
условиях могут иметь точно-линейную ФЧХ. Именно эти фильтры чаще всего
используются на практике. БИХ-фильтры не могут иметь точно-линейную ФЧХ, они
могут иметь только приближенно линейную ФЧХ.
и не искажают форму сигнала,
спектр которого находится в полосе пропускания. КИХ-фильтры при определенных
условиях могут иметь точно-линейную ФЧХ. Именно эти фильтры чаще всего
используются на практике. БИХ-фильтры не могут иметь точно-линейную ФЧХ, они
могут иметь только приближенно линейную ФЧХ.
При проектировании ЦФ используются реализационные критерии и критерии качества.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.