Формула (2.11) получила название прямого дискретного преобразования Фурье (ПДПФ).
![]() – это комплексные отсчеты спектра периодического дискретного
сигнала
– это комплексные отсчеты спектра периодического дискретного
сигнала ![]() .
Поскольку частота дискретизация спектра
.
Поскольку частота дискретизация спектра 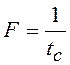 ,а
,а
![]() , то в интервале
, то в интервале ![]() будет укладываться
будет укладываться 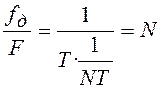 отсчетов спектра дискретного
сигнала
отсчетов спектра дискретного
сигнала ![]() .
.
Теперь обработку сигнала можно
осуществлять в частотной области, вводя в ЭВМ отсчеты ![]() спектра сигнала, что
значительно сокращает время обработки дискретного сигнала.
спектра сигнала, что
значительно сокращает время обработки дискретного сигнала.
Это фундаментальное для дискретных
сигналов соотношение представляет собой алгоритм вычисления гармонических
составляющих ![]() по заданным дискретным
отсчетам
по заданным дискретным
отсчетам ![]() аналогового
сигнала
аналогового
сигнала ![]() .
.
Отметим некоторые очевидные свойства ПДПФ.
1) Дискретное преобразование обладает свойствами линейности: сумме (разности) дискретных сигналов соответствует сумма (разность) их ДПФ.
2) Число определяемых коэффициентов ![]() :
: ![]() равно числу отсчетов N за
период сигнала
равно числу отсчетов N за
период сигнала ![]() . При
. При ![]() коэффициент
коэффициент ![]() .
.
3) Коэффициент ![]() (постоянная
составляющая) является средним значением всех отсчетов:
(постоянная
составляющая) является средним значением всех отсчетов:
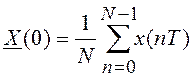 .
.
4) Если N – четное число, то
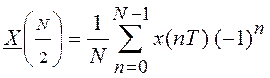 .
.
5) Коэффициенты ДПФ, номера которых
располагаются симметричного относительно ![]() образуют
сопряженные пары
образуют
сопряженные пары
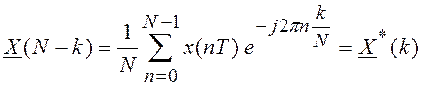 , т.е. можно
считать, что коэффициенты
, т.е. можно
считать, что коэффициенты 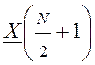 ,
, 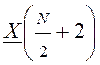 , …,
, …, ![]() соответствуют отрицательным
частотам (рисунок 2.13,в). При изучении спектра сигнала они не дают новых
сведений.
соответствуют отрицательным
частотам (рисунок 2.13,в). При изучении спектра сигнала они не дают новых
сведений.
При изучении теории ДПФ возникает
очевидный вопрос: можно ли по известным коэффициентом ДПФ ![]() вычислить отсчетные
значения
вычислить отсчетные
значения ![]() непрерывного сигнала? Да,
можно. В этом случае используется обратное дискретное преобразование Фурье
(ОДПФ):
непрерывного сигнала? Да,
можно. В этом случае используется обратное дискретное преобразование Фурье
(ОДПФ):
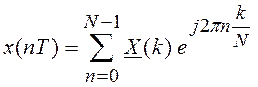 ,
, ![]() (2.12)
(2.12)
Формулы (2.11) и (2.12) являются аналогами прямого и обратного преобразования Фурье для непрерывных сигналов.
Перейдем к рассмотрению алгоритма ПДПФ и ОДПФ. Оба преобразования можно вычислить с помощью одного и того же алгоритма. Для этого значения выражения (2.11) и (2.12) запишем следующим образом:
|
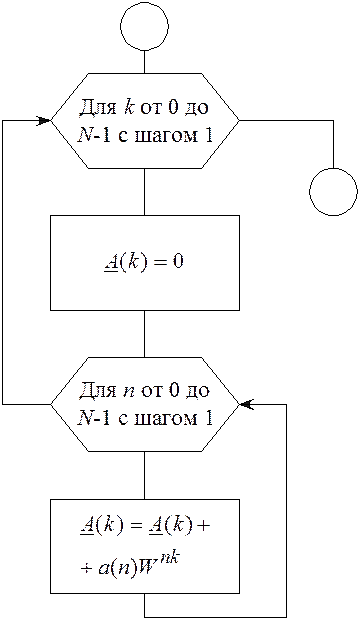
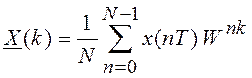 ;
; 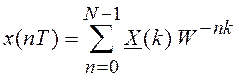 (2.13)
(2.13)
здесь 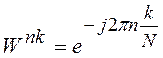 – поворачивающий множитель
(или ядро преобразования).
– поворачивающий множитель
(или ядро преобразования).
Пусть
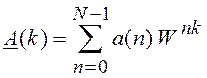 ,
, ![]() (2.14)
(2.14)
Далее для прямого ДПФ ![]() , а искомое
, а искомое 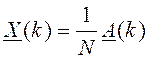 . При вычислении обратного ДПФ
. При вычислении обратного ДПФ ![]() ,
, ![]() ;
;
![]() , а искомое
, а искомое ![]() равно
равно ![]() .
.
Таким образом, для вычисления ДПФ и ОДПФ можно воспользоваться единым алгоритмом, предусматривающим расчет по выражению (2.14). Схема такого алгоритма приведена на рисунке 2.14.
Представленный на рисунке 2.14
алгоритм дискретного преобразования Фурье предусматривает большой объем
вычислений. Для вычислений одного значения ![]() требуется
N-кратное повторение внутреннего цикла и, таким образом, выполнение N
умножений (в общем случае пар комплексных чисел) и столько же сложений. А для
нахождения N значений
требуется
N-кратное повторение внутреннего цикла и, таким образом, выполнение N
умножений (в общем случае пар комплексных чисел) и столько же сложений. А для
нахождения N значений ![]() потребуется
N-кратное выполнение внешнего цикла, и число умножений будет равно
потребуется
N-кратное выполнение внешнего цикла, и число умножений будет равно ![]() (например, при обработке
речевых сигналов длина одного фрагмента достигает значения
(например, при обработке
речевых сигналов длина одного фрагмента достигает значения ![]() и требуется осуществить более
миллиона –
и требуется осуществить более
миллиона – ![]() умножений и сложений). Если
длины обрабатываемых массивов превышают тысячу единиц, то дискретная
спектральная обработка в реальном масштабе времени требует большой мощности и
сложности вычислений.
умножений и сложений). Если
длины обрабатываемых массивов превышают тысячу единиц, то дискретная
спектральная обработка в реальном масштабе времени требует большой мощности и
сложности вычислений.
Однако, алгоритм ДПФ содержит большое
количество избыточных операций, в том числе и таких, когда одни и те же
операции многократно выполняются над одними и теми же значениями величин. Это
связано со следующим: в выражении (2.14) вычисляемый поворачивающий множитель 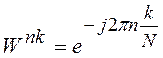 является периодической функцией
аргумента
является периодической функцией
аргумента ![]() . Так как п и k принимают значение из последовательности 0, 1, …, N-1, то
произведение
. Так как п и k принимают значение из последовательности 0, 1, …, N-1, то
произведение ![]() принимают значения 0, 1, …, N,
…, 2N, …,
принимают значения 0, 1, …, N,
…, 2N, …, ![]() и будут содержать
большое число периодов N. Соответствующие им значения
и будут содержать
большое число периодов N. Соответствующие им значения ![]() будут повторяться через период
N. В таблице 2.1 это показано для
будут повторяться через период
N. В таблице 2.1 это показано для ![]() .
.
Таблица 2.1
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.