Случай 1
Пусть при дискретизации сигнала с
частотой ![]() выполнялось условия
выполнялось условия
![]() (10.1)
(10.1)
(в нашем
случае ![]() ). Очевидно, что величина
частоты дискретизации является излишней, поскольку в соответствии с теоремой
Котельникова должно выполняться условие
). Очевидно, что величина
частоты дискретизации является излишней, поскольку в соответствии с теоремой
Котельникова должно выполняться условие ![]() .
Модуль спектра сигнала
.
Модуль спектра сигнала ![]() с частотой
с частотой 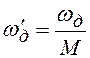 показан на рисунке 10.2,в. Он
периодичен с частотой
показан на рисунке 10.2,в. Он
периодичен с частотой 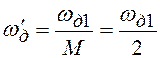 . Поскольку
в интересующей нас полосе
. Поскольку
в интересующей нас полосе ![]() спектр не
изменяется, то как по сигналу
спектр не
изменяется, то как по сигналу ![]() , так и по
сигналу
, так и по
сигналу ![]() можно восстановить исходный
сигнал
можно восстановить исходный
сигнал ![]() .
.
Очевидно, что сигнал ![]() можно получить из сигнала
можно получить из сигнала ![]() путем прореживания последнего,
т.е. путем взятия только каждого M-го (в нашем случае каждого 2-го)
отсчета из сигнала
путем прореживания последнего,
т.е. путем взятия только каждого M-го (в нашем случае каждого 2-го)
отсчета из сигнала ![]() . Эта операция
называется децимацией с целочисленным коэффициентом M.
. Эта операция
называется децимацией с целочисленным коэффициентом M.
Случай 2.
Пусть при дискретизации частотой ![]() не выполнялось условие
не выполнялось условие ![]() . Тогда при
. Тогда при 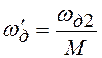 на основной спектр в полосе
частот
на основной спектр в полосе
частот ![]() наложится дополнительный
спектр, расположенный около центральной частоты
наложится дополнительный
спектр, расположенный около центральной частоты ![]() (рисунок
10.2,г). Следовательно, спектр сигнала и сам сигнал оказались искаженными. Если
по сигналу
(рисунок
10.2,г). Следовательно, спектр сигнала и сам сигнал оказались искаженными. Если
по сигналу ![]() можно восстановить сигнал
можно восстановить сигнал ![]() , то по сигналу
, то по сигналу ![]() этого сделать уже невозможно.
этого сделать уже невозможно.
Т.о. для выполнения операции децимации
в целое число раз M необходимо, чтобы частота дискретизации ![]() исходного сигнала, подлежащего
децимации удовлетворила условию:
исходного сигнала, подлежащего
децимации удовлетворила условию:
![]() (10.2)
(10.2)
где ![]() –
граничная частота спектра сигнала.
–
граничная частота спектра сигнала.
Из рисунка видно, что если основной
спектр входного сигнала условно разбить на M составляющих ![]() (в примере M = 3),
занимающих по оси частот M полос шириной в
(в примере M = 3),
занимающих по оси частот M полос шириной в ![]() ,
то после уменьшения частоты дискретизации в M раз в основную полосу
частот
,
то после уменьшения частоты дискретизации в M раз в основную полосу
частот 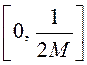 .
.
Собственно, операция децимации выполняется с помощью компрессора частоты дискретизации (КЧД). Условное изображение КЧД, осуществляющего уменьшение частоты дискретизации в M раз показано на рисунке 10.4.
КЧД
представляет собой ключ, который замыкается в моменты времени ![]() при
при ![]() , т.е. из входного сигнала
, т.е. из входного сигнала ![]() с интервалом
с интервалом
|
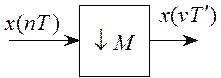
дискретизации Т
берется только каждый M-й отсчет и формируется выходной сигнал с ![]() , иными свойствами выходная
последовательность КЧД
, иными свойствами выходная
последовательность КЧД ![]() формируется путем
прореживания входной последовательности
формируется путем
прореживания входной последовательности ![]() по
алгоритму
по
алгоритму
![]() ,
(10.2)
,
(10.2)
где ![]() ;
;
![]() ;
;
k – целое число ![]() .
.
Операция, выполняемая КЧД, называется
прореживанием, а последовательность ![]() –
прореженной.
–
прореженной.
На рисунке 10.5 показаны
последовательности ![]() и
и ![]() для случая
для случая ![]() и
и ![]() ,
т.е. при уменьшении частоты дискретизации в 4 раза.
,
т.е. при уменьшении частоты дискретизации в 4 раза.
На практике часто используется случай ![]() . Можно показать, что в этом
случае спектр выходной последовательности КЧД
. Можно показать, что в этом
случае спектр выходной последовательности КЧД ![]() равен
равен
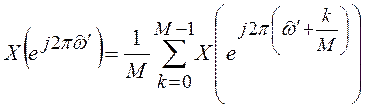 ,
(10.3)
,
(10.3)
|
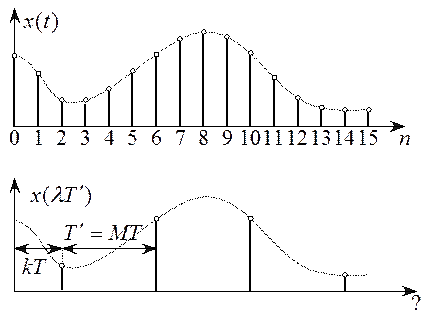
где 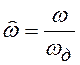 – нормированная частота
спектра входной последовательности;
– нормированная частота
спектра входной последовательности;
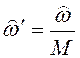 – нормированная частота
спектра выходной последовательности.
– нормированная частота
спектра выходной последовательности.
Из (10.3) видно, что спектр
выходной последовательности есть сумма спектров входного сигнала, сдвинутых
один относительно другого по оси частот на величину ![]() . Таким образом, если основной
спектр входного сигнала КЧД в полосе
. Таким образом, если основной
спектр входного сигнала КЧД в полосе ![]() разбить
условно на M составляющих, занимающих M полос на оси частот
шириной
разбить
условно на M составляющих, занимающих M полос на оси частот
шириной ![]() , то после уменьшения частоты
дискретизации в M раз в основную полосу частот
, то после уменьшения частоты
дискретизации в M раз в основную полосу частот 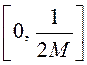 выходного сигнала показывает
каждая k-я составляющая
спектра входного сигнала из полосы
выходного сигнала показывает
каждая k-я составляющая
спектра входного сигнала из полосы 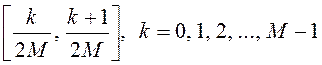 .
.
На рисунке 10.6 показаны модули спектра входного сигнала и составляющих спектра выходного сигнала КДЧ при уменьшении частоты дискретизации в M = 3 раза.
|
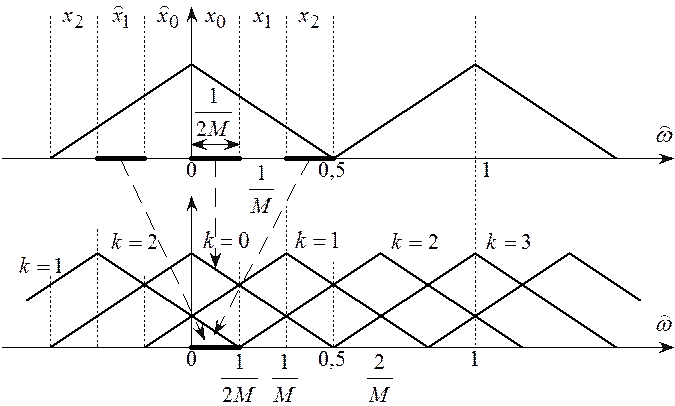
выходной
последовательности показывают прямые спектры выходной последовательности
попадают прямые спектры ![]() четных
составляющих
четных
составляющих ![]() и инверсные спектры
и инверсные спектры
![]() нечетных составляющих
нечетных составляющих ![]() спектра входной
последовательности. В нашем случае спектр входной последовательности условно
разбит на три составляющие
спектра входной
последовательности. В нашем случае спектр входной последовательности условно
разбит на три составляющие ![]() ,
, ![]() ,
, ![]() .
После уменьшения частоты дискретизации в 3 раза в основную полосу частот
.
После уменьшения частоты дискретизации в 3 раза в основную полосу частот 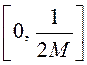 попадают составляющие
попадают составляющие ![]() и
и ![]() при
при
![]() и
и ![]() при
при
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.