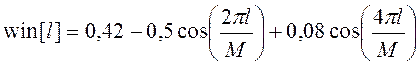Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 20

, – окно Блэкмана;        (6.9)

Эти окна отличаются тем, что для их преобразований Фурье боковые лепестки выражены менее ярко. На рисунке 6.3,б показано преобразование Фурье от функции Хэмминга. Как видим, уровень боковых лепестков в полосе задерживания существенно уменьшился.

Выбор конкретного окна зависит от предъявляемых к фильтру требований.

Формула для расчета коэффициентов КИХ-фильтров нижних частот имеет вид:

.

6.4.2 Проектирование КИХ-фильтров с точной линейной ФЧХ общего вида

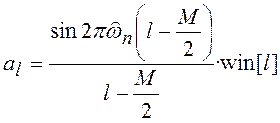Существует четыре вида фильтров с точно линейной ФЧХ и передаточной функцией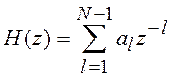

-  фильтр вида 1: N – нечетное;  (симметричные коэффициенты);

-  фильтр вида 2: N – четное; ;  (симметричные коэффициенты);

-  фильтр вида 3: N – нечетное;  (антисимметричные коэффициенты);

-  фильтр вида 4: N – четное; ;  (антисимметричные коэффициенты).

Например, для первого вида:

.

Рассмотрим фильтр первого вида. Можно показать, что подбором соответствующей величины весового коэффициента  характеристики фильтров 2, 3 и 4 типов могут быть сведены к характеристикам фильтров 1-го вида. Поэтому в дальнейшем будем рассматривать фильтры этого вида.

Выполнив замену переменной , и учтя, что коэффициенты фильтра симметричные, получим:

,

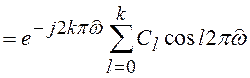где 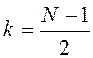,                                            (6.10)

Т.о. , где

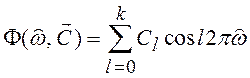                                 (6.11)

 – точно линейная.

Выражение (6.11) соответствует разложению  в ряд Фурье. Тогда коэффициенты этого ряда  определяются как

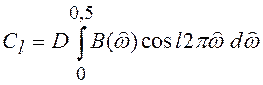,                                    (6.12)

где , при  и  для ;

 – аппроксимируемая функция.

Определим аппроксимируемую функцию следующим образом:

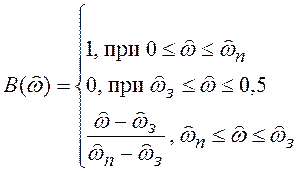                              (6.13)

Функция  доопределена в промежуточной полосе, чтобы обеспечить ее непрерывность в промежутке  и тем самым исключить явление Гиббса.

При таком определении  из (6.12) получим:

Рисунок 6.4

;

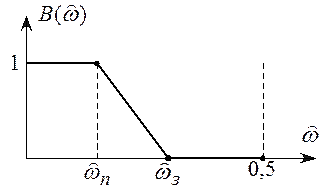
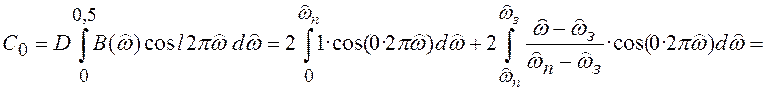
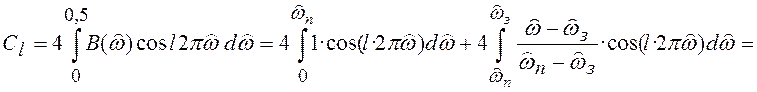
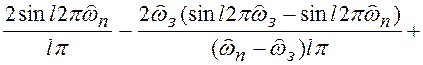
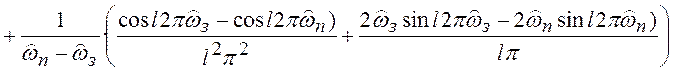,      (6.14)

при .

Этот расчет может быть выполнен на любой ЭВМ. После определения коэффициентов  рассчитываются коэффициенты передаточной функции , причем для фильтра первого типа

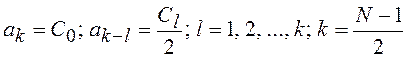,                        (6.15)

а затем АЧХ фильтра по формуле

.

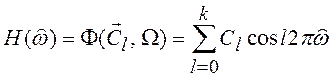Сравнивая найденную АЧХ с требуемой, делают вывод о соответствии характеристик фильтра требуемым. Если условие

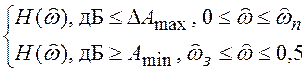
не выполняется при выбранном значении k (а значит и порядке фильтра N), то k увеличивают и весь расчет повторяют заново.

6.4.3 Метод наименьших квадратов

Решим задачу 3, т.е. потребуем, чтобы

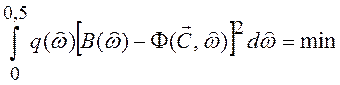                            (6.16)

Этот критерий соответствует минимуму среднеквадратичной ошибки и получил название метода наименьших квадратов. Здесь

 – аппроксимируемая функция;

 – аппроксимирующая функция;

 – вектор коэффициентов С: , через которые рассчитываются коэффициенты передаточной функции фильтра : ;

 – весовая функция. Она позволяет регулировать точность аппроксимации. Для тех интервалов, где значения  больше – точность аппроксимации выше, а где меньше – ниже.

Необходимое и достаточное условие минимума выражения (6.16)

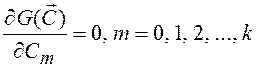                             (6.17)

Выражение (6.17) представляет собой систему линейных уравнений, относительно неизвестных коэффициентов . Решив эту систему, находят коэффициенты , а по ним рассчитывают коэффициенты передаточной функции . Расчетные формулы для  находят из (6.15):

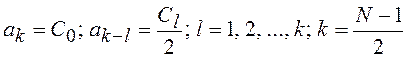
Расчет коэффициентов  требует определения коэффициентов системы линейных уравнений и решение этой системы. Этот расчет может быть выполнен на любой ЭВМ.

6.4.4 Метод наименьшей равномерной (чебышевской) аппроксимации

Этот метод аппроксимации предполагает расчет вспомогательных коэффициентов  из условия минимума величины

, где ;                                                            (6.18)

;

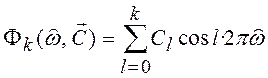 – вектор коэффициентов ;

 – весовая функция.

Функцию , удовлетворяющую условию (6.18) при заданных  и k называют функцией наилучшего равномерного приближения среди подобных других функций, отличающихся от нее лишь значением коэффициентов .