Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 24

Поэтому при реализации ЦФ следует учитывать поведение упомянутых ошибок, которые часто называют ошибками квантования. На входе цифровой системы ошибки квантования воспринимаются в виде шума, который называют шумом квантования. Это значит, что выбранная структура ЦФ, разрядность входных и выходных сигналов, длина регистров арифметических устройств должны быть определены так, чтобы ошибки квантования не превышали допустимой величины.

7.2 Эффекты квантования коэффициентов фильтра. Расчет разрядности коэффициентов

Коэффициенты передаточной функции фильтра  и  являются сомножителями при вычислении отсчетов выходного сигнала фильтра.

АЧХ фильтра  нормируется так, чтобы при всех значениях  в полосе пропускания , а в полосе задерживания , поэтому для избирательных фильтров справедливо:

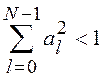, т.е.                                         (7.1)

В силу этого двоичный код коэффициентов КИХ-фильтров содержит лишь знаковый разряд и дробную часть, и не содержит целой части.

Поскольку десятичные числа менее единицы в двоичном коде представит точно невозможно, то найденные “точные”, т.е. представленные семью-четырнадцатью десятичными знаками цифровые коэффициенты фильтров  заменяются приближенным представлением в двоичном коде. Процесс округления вносит некоторую погрешность и вместо точного значения  используются их приближенные значения .

Для избирательного фильтра, АЧХ которого должна удовлетворять условию  при , критерием возможности округления коэффициентов до  двоичных разрядов является неравенство:

 для ,                     (7.2)

где  – АЧХ фильтра, рассчитанное при округлении коэффициентов до  двоичных разрядов.

 – АЧХ фильтра с неквантованными коэффициентами.

Существуют разные способы расчета разрядности коэффициентов  по допускам на характеристики фильтров. Самый простой способ – метод проб. Расчет минимального значения  по методу проб начинается с выбора разрядности ориентировочно, субъективно. Затем следует расчет АЧХ с новыми – приближенными значениями коэффициентов, оценка искажений характеристики по (7.2) и соответствующая коррекция разрядности коэффициентов  в ту или иную сторону. Расчет повторяется столько раз, сколько потребуется для удовлетворительного решения задачи по выбору разрядности коэффициентов.

В нерекурсивных ЦФ частотные характеристики линейно связаны с коэффициентами фильтров. Поэтому малые искажения коэффициентов приводят к малым искажениям частотных характеристик и проблемы, связанные с округлением коэффициентов возникают редко. Однако, если фильтр должен иметь очень крутой спад АЧХ между полосами пропускания и задерживания, округление коэффициентов все же может привести к заметным искажениям частотных характеристик.

Значительно серьезнее округления коэффициентов сказывается на характеристиках рекурсивных фильтров, поскольку коэффициенты знаменателя передаточной функции связаны с импульсными характеристиками нелинейно. Как правило, наибольшие искажения происходят в тех случаях, когда АЧХ фильтра имеет крутые скаты в переходных зонах между полосами пропускания и задерживания. Величина этих искажений сильно зависит от формы реализации фильтра. При представлении фильтра в виде каскадного соединения звеньев второго порядка округление коэффициентов влияет на характеристики фильтров значительно слабее, чем при прямой форме реализации.

Таким образом, прослеживается общая закономерность: параметры любого фильтра с резким изменением частотной характеристики в переходной полосе, реализованного в прямой форме, крайне чувствительны к значениям коэффициентов фильтра.

7.3 Расчет разрядности регистров оперативной памяти

В регистрах оперативной памяти хранятся отсчеты входного и выходного сигналов и результаты промежуточных вычислений.

Значение разрядности регистров оперативной памяти фильтра зависит в общем случае от формы реализации фильтра и способа представления чисел. Для упрощения построения аппаратной части сделаны следующие допущения: