Рассмотрим теперь условия,
накладываемые на ширину спектра входной последовательности на оси частот, при
которой уменьшение частоты дискретизации не приведет к наложению спектров. Как
видно из рисунка 10.6 и из (10.3) наложение спектров отсутствует, если спектр
входного сигнала занимает не весь частотный диапазон ![]() , а лишь одну из его полос
шириной
, а лишь одну из его полос
шириной
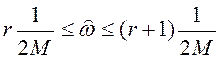 ,
(10.4)
,
(10.4)
где ![]() , или часть этой полосы.
, или часть этой полосы.
Условие (10.4) соответствует обобщенной теореме Котельникова, устанавливающей связь между шириной спектра и частотой дискретизации сигнала.
Простейшая система уменьшения частоты дискретизации в целое число раз имеет вид, показанный на рисунке 10.6.
Рассмотрим принцип работы схемы при M = 3.
Предполагается, что спектр входного сигнала ![]() занимает
не всю полосу частот
занимает
не всю полосу частот ![]() , а то-
, а то-
|
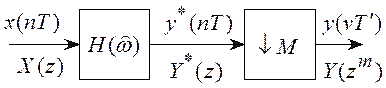
лько ее часть ![]() (рисунок 10.7,а). Задачей
схемы является уменьшение частоты дискретизации в M раз с сохранением
спектра, расположенного в части полосы
(рисунок 10.7,а). Задачей
схемы является уменьшение частоты дискретизации в M раз с сохранением
спектра, расположенного в части полосы ![]() от
0 до
от
0 до ![]() .
.
Собственно операция уменьшения частоты
дискретизации в M раз осуществляется с помощью КЧД, формирующего сигнал ![]() , путем взятия каждого М-отсчета
из последовательности
, путем взятия каждого М-отсчета
из последовательности ![]() , т.е.
, т.е. ![]() ,
, ![]() Для
предотвращения явления наложения спектров операции, выполняемой КЧД,
предшествует операция цифровой фильтрации децимируемого сигнала. Входной сигнал
Для
предотвращения явления наложения спектров операции, выполняемой КЧД,
предшествует операция цифровой фильтрации децимируемого сигнала. Входной сигнал
![]() обрабатывается фильтром,
назначение которого состоит в подавлении частот составляющих
обрабатывается фильтром,
назначение которого состоит в подавлении частот составляющих
|
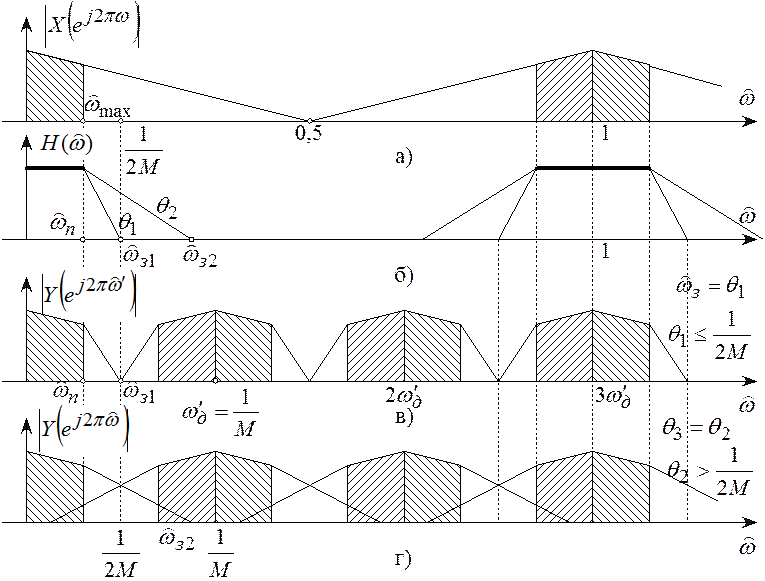
спектра
входного сигнала в диапазонах 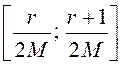 , где
, где ![]() , которые при последующем
уменьшении частоты дискретизации попадут в частотный диапазон
, которые при последующем
уменьшении частоты дискретизации попадут в частотный диапазон 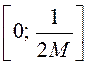 . Идеализированная АЧХ фильтра
НЧ схемы должна увеличивать требованиям:
. Идеализированная АЧХ фильтра
НЧ схемы должна увеличивать требованиям:
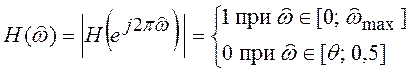 (10.5)
(10.5)
где 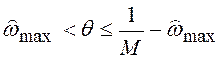 ;
; ![]() является
граничной частотой полосы задерживания ФНЧ (рисунок 10.7,б). Если АЧХ фильтра
удовлетворяет условию (10.5), то в полосе частот
является
граничной частотой полосы задерживания ФНЧ (рисунок 10.7,б). Если АЧХ фильтра
удовлетворяет условию (10.5), то в полосе частот ![]() спектр
выходного сигнала равен спектру входного сигнала. В полосе частот
спектр
выходного сигнала равен спектру входного сигнала. В полосе частот 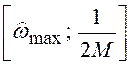 может отсутствовать положение
спектров при
может отсутствовать положение
спектров при 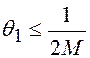 , либо могут иметь
место наложения спектров при
, либо могут иметь
место наложения спектров при 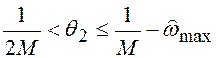 .
.
Оба случая допустимы, поскольку от
схемы требуется только сохранение спектра в полосе частот ![]() . Требования к АЧХ могут быть
значительно ослаблены, если
. Требования к АЧХ могут быть
значительно ослаблены, если 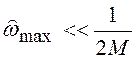 .
.
Рассмотрим теперь особенности использования ЦФ с КИХ и БИХ при децимации.
Передаточная функция ![]() (как КИХ, так и БИХ-фильтра) и
его частотная характеристика определяется “высокой” входной частотой
дискретизации
(как КИХ, так и БИХ-фильтра) и
его частотная характеристика определяется “высокой” входной частотой
дискретизации ![]() . Однако КИХ фильтр
фактически работает на “низкой” выходной частоте, поскольку нет необходимости
рассчитывать M – 1 отсчетов входной последовательности
. Однако КИХ фильтр
фактически работает на “низкой” выходной частоте, поскольку нет необходимости
рассчитывать M – 1 отсчетов входной последовательности ![]() фильтра, которые будут
отброшены КЧД.
фильтра, которые будут
отброшены КЧД.
БИХ-фильтр в системах децимации
работает на “высокой” частоте дискретизации, поскольку при вычислении любого
отсчета последовательности ![]() необходимо
иметь значения всех предыдущих отсчетов, в том числе и тех, которые должны
будут отброшены КЧД.
необходимо
иметь значения всех предыдущих отсчетов, в том числе и тех, которые должны
будут отброшены КЧД.
Однако БИХ-фильтры предпочтительнее, если следует минимизировать емкость оперативной памяти или объем оборудования.
Число операций умножения в единицу
времени для КИХ фильтров 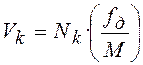 , для БИХ
фильтров
, для БИХ
фильтров ![]() , где
, где ![]() и
и ![]() –
количество коэффициентов в числителе и знаменателе передаточной функции БИХ
фильтра;
–
количество коэффициентов в числителе и знаменателе передаточной функции БИХ
фильтра; ![]() – количество коэффициентов
передаточной функции КИХ-фильтра,
– количество коэффициентов
передаточной функции КИХ-фильтра, ![]() – частота
дискретизации.
– частота
дискретизации.
Применения БИХ фильтров оказывается
предпочтительнее по критерию минимума операций умножения в единицу времени при
условии ![]() .
.
При требовании сохранения фазовых соотношений между составляющими спектра сигнала в полосе частот целесообразно использовать КИХ-фильтр с линейной ФЧХ.
Рассмотрим структурную схему системы децимации при использовании в схеме КИХ фильтра с передаточной функцией
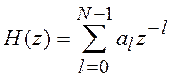 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.