Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 5

Рисунок 2.1-Типы сигналов

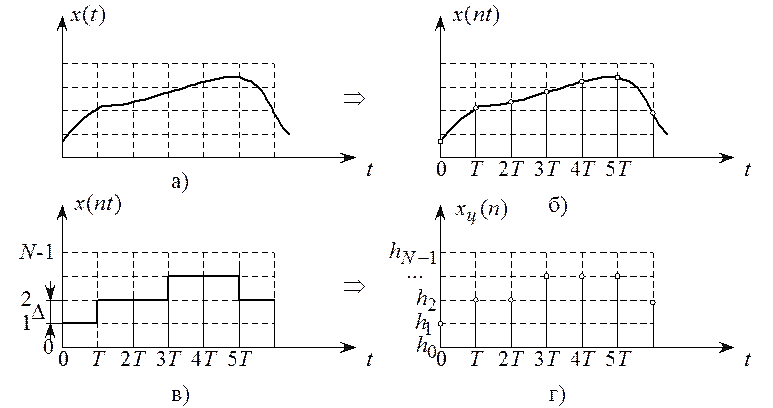
Таблица 2.1-Типы сигналов

Сигнал	Рисунок	Область определения	Область значений
Аналоговый	2.1,а	непрерывная	непрерывная
Дискретный	2.1,б	дискретная	непрерывная
Квантованный	2.1,в	непрерывная	дискретная
Цифровой	2.1,г	дискретная	дискретная

; ; ; .

Цифровые сигналы. Для того, чтобы представить дискретный сигнал последовательностью чисел конечной разрядности его следует подвергнуть операции, которая называется квантованием. Вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности.

Расстояния между этими уровнями называется шагом квантования  (рисунок 2.1,в). Число этих уровней равно N (от 0 до N-1). Каждому уровню присваивается некоторое число: . Отсчеты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования (рисунок 2.1,г).

Каждый уровень квантования кодируется двоичным числом с п разрядами, например: ; ;  и т.д. Число уровней квантования и наименьшее число разрядов п двоичный чисел, кодирующих эти уровни, связаны соотношением

,

N=4	п=2
N=6	п=3
N=9	п=4
N=32	п=5	и т.д.

Например, при

Если кодируемая функция может принимать как отрицательные, так и положительные значения, то знак функции кодируется, как правило, с помощью специального знакового разряда. Пример цифровых сигналов – сигналы импульсно-кодовой модуляции, использующиеся в системах многоканальной связи.

Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых.

Единичный ступенчатый сигнал (рисунок 2.2) в аналоговой форме:

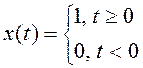
В дискретной форме:

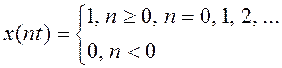
 – сдвинутая последовательность – образуется при сдвиге последовательность вправо при  и влево при .

Импульс Дирака или -функция (рисунок 2.3) в аналоговой форме:

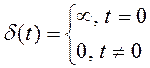
В дискретной форме:

Рисунок 2.2-Единичные сигналы: а) аналоговый; б) дискретный; в) дискретный, сдвинутый на два такта

Рисунок 2.3-Функция Диракка: а) аналоговая; б) дискретная; в) дискретная, сдвинутая на два такта

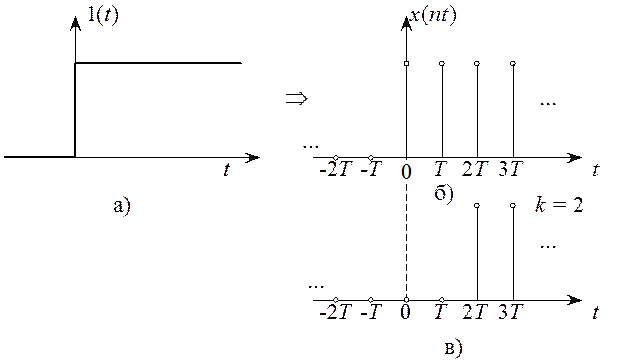
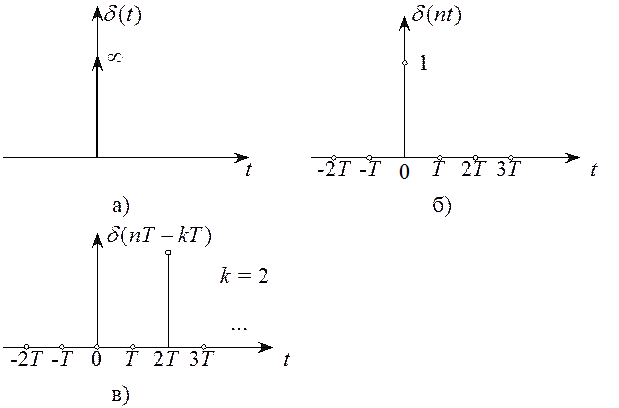
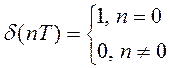
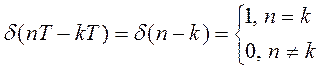
Тогда математическая запись любого дискретного сигнала имеет вид:

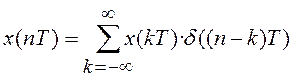,                          (2.1)

Рисунок 2.4

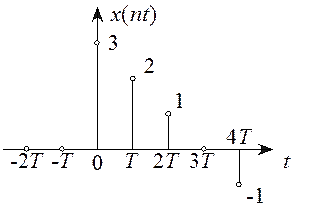
т.к. все члены при  равны 0. Например, последовательность  (рисунок 2.4) может быть записана в виде:

.

Итак, согласно выражению (2.1) дискретный сигнал представляет -функций, следующих с интервалом времени Т. Эти функции имеют амплитудные коэффициенты, равные отсчетам сигнала  в точках дискретизации .

Как часто следует брать отсчеты? Их следует брать так часто, чтобы успевать отследить все, даже самые быстрые изменения сигнала. Иначе, при восстановлении этого сигнала по дискретизированным отсчетам часть информации будет потеряна и форма восстановленного сигнала  (рисунок 2.6,а) будет отличаться от формы исходного  сигнала (рисунок 2.6,а).

Периодической называют последовательность  удовлетворяющей условию:

, где

Рисунок 2.5

	Рисунок 2.6

 

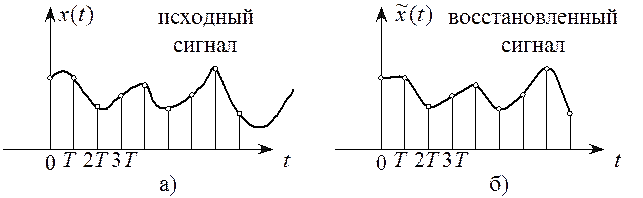
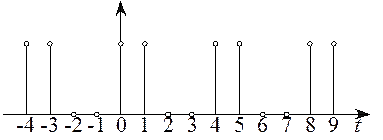
m и N – целые числа,

m= 1, 2, …; NТ – период последовательности.

Например, для N = 4 получили последовательность, приведенную на рисунке 2.6. Периодичную последовательность достаточно задать на интервале