Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 23

Рассмотренное билинейное преобразование вида (6.21) позволило получить передаточную функцию цифрового ФНЧ. Существует более общее преобразование, позволяющее преобразовать аналоговый ФНЧ в избирательный БИХ-фильтр любого типа (ФНЧ, ФВЧ, ПФ, РФ). Не рассматривая вывода соответствующих формул, приводим их в таблице 6.1.

Здесь последовательно указаны нормированные значения граничных частот цифрового фильтра, формулы замены переменной в , формулы для расчета параметра , позволяющие получить по заданным  и  нормированный аналоговый прототип с частотами среза  и, наконец, формула для расчета граничной частоты полосы задерживания  ( определять не надо, т.к. она всегда равна 1). Для ПФ и РФ расчет  выполняется по двум формулам и из двух значений  и  выбирается то, модуль которого наименьший.

Пример 5.1 Рассчитать дискретный фильтр НЧ с параметрами:  кГц;  кГц;  кГц;  дБ;  дБ.

По формуле (6.24) находим

.

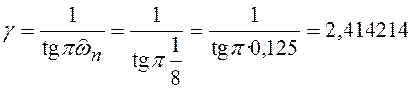Далее находим нормированную частоту задерживания аналогового ФНЧ-прототипа

.

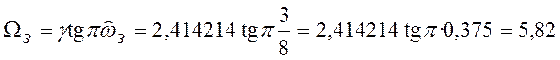Тем самым произведен перерасчет требований, предъявленных к дискретному фильтру в требования к аналоговому прототипу.

Таблица 6.1

Цифровой фильтр	Граничные “цифровые” частоты	Формула замены	Параметр	Связь “аналоговых” частот с “цифровыми”	Граничные “аналоговые” частоты
Нижних частот
Верхних частот
Полосовой	,				, где
Режекторный	,				, где

Рисунок 6.10

Как рассчитать аналоговый фильтр-прототип? Исходными требованиями для расчета являются требования к НЧ-прототипу (рисунок 6.10,б). По ним, пользуясь любым справочником по расчету аналоговых фильтров, рассчитывают передаточную функцию аналогового фильтра-прототипа.

Пример 6.2 Для ,  дБ,  дБ (параметры ФНЧ-прототипа, взятые из предыдущего примера), пользуясь справочником, находим, что

.

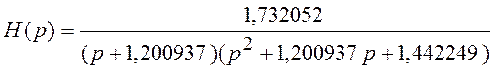Как осуществить переход к дискретному фильтру? Для перехода от  к  воспользуемся билинейным преобразованием

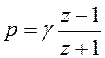
Для рассмотренного выше примера , поэтому 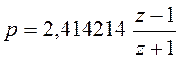. Подставляем это выражение в выражение . Получим

.

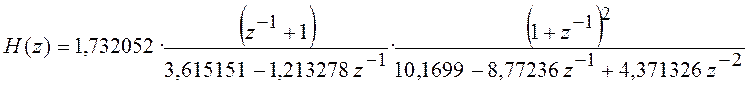Дискретный фильтр с такой передаточной функцией  легко реализовать в виде каскадного соединения типовых звеньев 1-го и 2 порядка. Для этого функцию  перепишем в виде

.

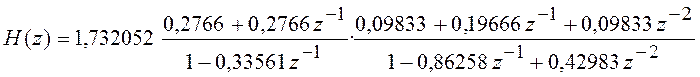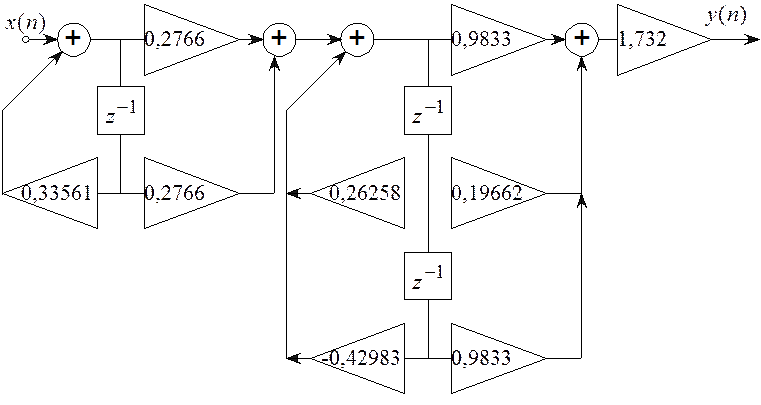
Схема фильтра, имеющего такую передаточную функцию приведена на рисунке 6.11.

Рисунок 6.11

 

7 Эффекты квантования в цифровых системах

7.1 Основные понятия

В разделе “Аналоговые, дискретные и цифровые сигналы” главы 1 мы обсуждали разницу между дискретными и цифровыми сигналами. До сих пор, строго говоря, речь шла о дискретных сигналах и системах, поскольку отсчеты сигналов и коэффициентов фильтров считались представленными точно (без погрешностей). Сигналы на входе  и выходе  ЦФ являются цифровыми, т.е. последовательностями чисел. Каждое из этих чисел представляется в виде двоичного кода, и в ЦФ в соответствии с алгоритмом

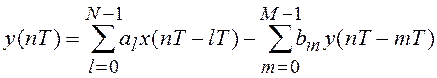
выполняются операции пересылки, сложения и умножения кодов. Представить числа точно конечным числом разрядов кода невозможно. При этом алгоритм функционирования реализуется неточно. Ошибки цифровой фильтрации обусловлены следующими факторами:

-  ошибки квантования входных и выходных сигналов;

-  квантованием коэффициентов фильтра  и ;

-  конечной разрядностью операционных устройств;

-  округлением промежуточных результатов вычислений.