Для описания аналоговых и дискретных
сигналов в частотной области используется аппарат преобразования Фурье.
Спектром ![]() аналогового сигнала
аналогового сигнала ![]() называют прямое преобразование
Фурье
называют прямое преобразование
Фурье
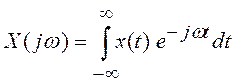 ,
(2.2)
,
(2.2)
где ![]() –
комплексная спектральная плотность.
–
комплексная спектральная плотность.
В свою очередь сигнал ![]() может быть восстановлен по его
спектру (обратное преобразование Фурье):
может быть восстановлен по его
спектру (обратное преобразование Фурье):
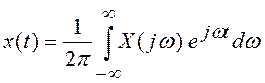 .
(2.3)
.
(2.3)
В соответствии с принципом
неопределенности сигнал ![]() , имеющий ограниченную протяженность во времени (рисунок 2.7,а) имеет
неограниченный по полосе спектр
, имеющий ограниченную протяженность во времени (рисунок 2.7,а) имеет
неограниченный по полосе спектр ![]() (рисунок 2.7,б) и наоборот (рисунок 2.7,в, г).
(рисунок 2.7,б) и наоборот (рисунок 2.7,в, г).
|
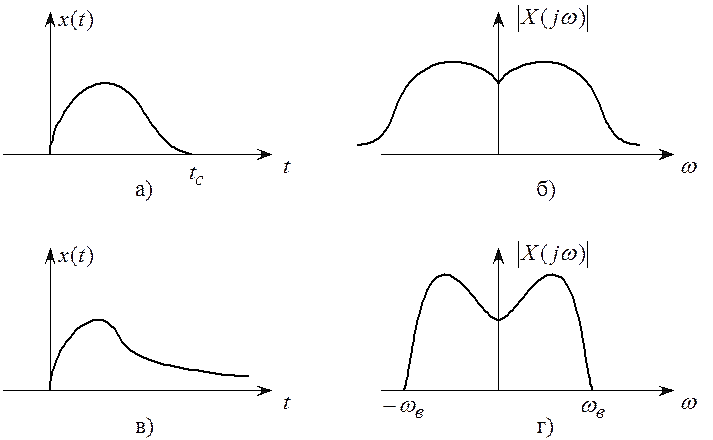
Здесь ![]() –
модуль комплексной спектральной плотности
–
модуль комплексной спектральной плотности ![]() , или спектр амплитуд. Как следует из этих рисунков, непериодический
сигнал бесконечной протяженности во времени имеет сплошной спектр, ограниченный
по частоте.
, или спектр амплитуд. Как следует из этих рисунков, непериодический
сигнал бесконечной протяженности во времени имеет сплошной спектр, ограниченный
по частоте.
Если сигнал ![]() является периодическим с
периодом
является периодическим с
периодом ![]() , равным его длительности
(рисунок 2.8,а), то его спектр будет дискретным (рисунок 2.8,б).
, равным его длительности
(рисунок 2.8,а), то его спектр будет дискретным (рисунок 2.8,б).
Теперь вместо ![]() используют отсчеты
используют отсчеты ![]() . Интервал дискретизации
спектра по частоте F определяется, как известно, периодом сигнала, в
данном случае
. Интервал дискретизации
спектра по частоте F определяется, как известно, периодом сигнала, в
данном случае 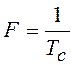 . Формула для прямого
и обратного преобразования Фурье получаются из (2.2) и (2.3) путем замены
непрерывной частоты f на дискретные значения пF.
. Формула для прямого
и обратного преобразования Фурье получаются из (2.2) и (2.3) путем замены
непрерывной частоты f на дискретные значения пF.
Таким образом, спектр ![]() периодического сигнала
вычисляется по формуле
периодического сигнала
вычисляется по формуле
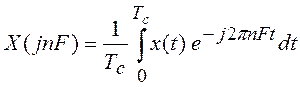 , (2.4)
, (2.4)
|
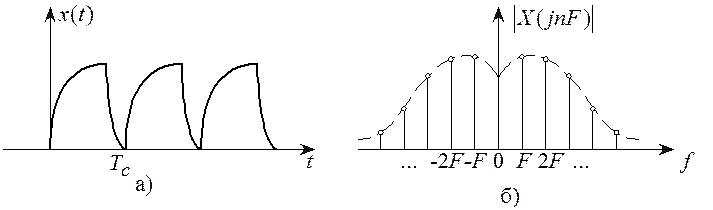
где ![]() -
комплексная амплитуда п-й гармоники.
-
комплексная амплитуда п-й гармоники.
Сигнал ![]() можно
восстановить по его дискретному спектру, воспользовавшись формулой
можно
восстановить по его дискретному спектру, воспользовавшись формулой
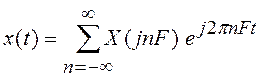 (2.5)
(2.5)
Выражение (2.5) является комплексным представлением ряда Фурье. Из соотношения (2.5) нетрудно увидеть, что спектральное представление периодического сигнала комплексной формой ряда Фурье содержит как положительные, так и отрицательные частоты. Однако, отрицательных частот в природе не существует, и это не реальное понятие, а математическая абстракция. Они появляются как следствие формального представления гармонических колебаний комплексной формой записи.
Легко доказать, что при переходе к тригонометрической форме записи
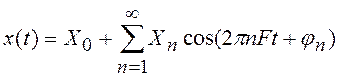 , где
, где 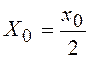 ;
;
![]()
понятие “отрицательная частота” теряет смысл.
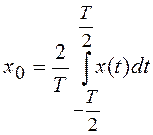 ,
,
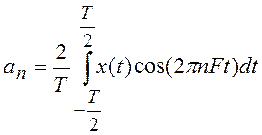 ,
,
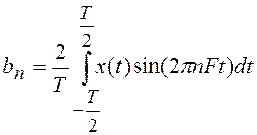 .
.
В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал (рисунок 2.9).
Обозначая период повторения спектра
дискретного сигнала ![]() , получим интервал
дискретизации
, получим интервал
дискретизации 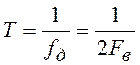 . Формулы прямого и
обратного преобразования Фурье для дискретного сигнала имеют вид:
. Формулы прямого и
обратного преобразования Фурье для дискретного сигнала имеют вид:
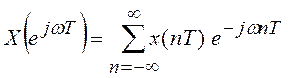 ,
(2.6)
,
(2.6)
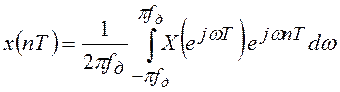 ,
(2.7)
,
(2.7)
Величину ![]() называют
комплексной спектральной плотностью дискретного сигнала.
называют
комплексной спектральной плотностью дискретного сигнала.
Пример 2.1 Рассчитать спектр дискретного сигнала ![]() ,
состоящего из одного отсчета:
,
состоящего из одного отсчета: ![]() .
.
Согласно (2.6) получим:
|
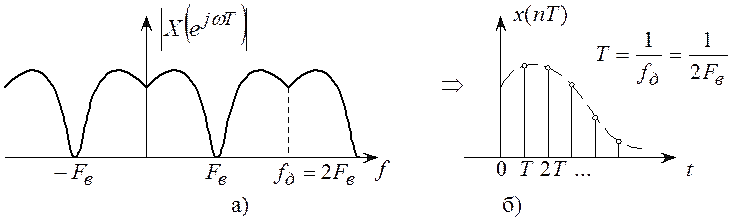
|

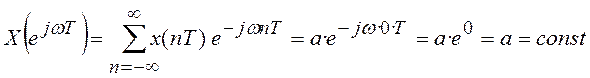
На рисунке 2.10,а приведен дискретный
сигнал, состоящий из одного отсчета ![]() , а на
рисунке 2.10,б соответствующий этому сигналу спектр
, а на
рисунке 2.10,б соответствующий этому сигналу спектр 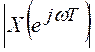 .
.
Отметим ряд свойств спектров дискретных сигналов.
1) Из (2.6) следует, что спектр
непериодического дискретного сигнала является непрерывной периодической
функцией по частоте ![]() с периодом
повторения, равным частоте дискретизации
с периодом
повторения, равным частоте дискретизации 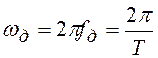 :
:
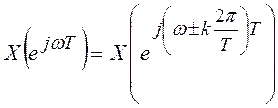 ,
, ![]() (2.8)
(2.8)
Ясно, что также периодическими
являются модуль спектра 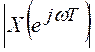 и его фаза -
и его фаза - ![]() . Кроме того, для вещественных последовательностей
. Кроме того, для вещественных последовательностей ![]() справедливо:
справедливо: 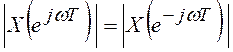 ;
; ![]() , т.е. модуль спектра вещественной
последовательности является четной функцией частоты, а аргумент – нечетной
функцией.
, т.е. модуль спектра вещественной
последовательности является четной функцией частоты, а аргумент – нечетной
функцией.
На рисунке 2.11 показано условное изображение модуля спектра дискретного сигнала.
Основным прямым спектром
![]() называют часть
спектра
называют часть
спектра ![]() ,
расположенную в области нижних частот от
,
расположенную в области нижних частот от ![]() ,
до
,
до 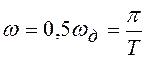 , а основным инверсным спектром
, а основным инверсным спектром
![]() – часть спектра
в области частот
– часть спектра
в области частот 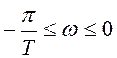 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.