Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 12

Элемент задержки (рисунок 4.3,в) осуществляет задержку цифрового сигнала на один интервал дискретизации.

Рисунок 4.3

 

Рисунок 4.4

 

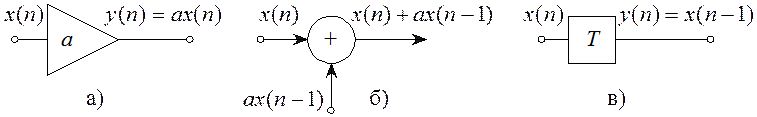
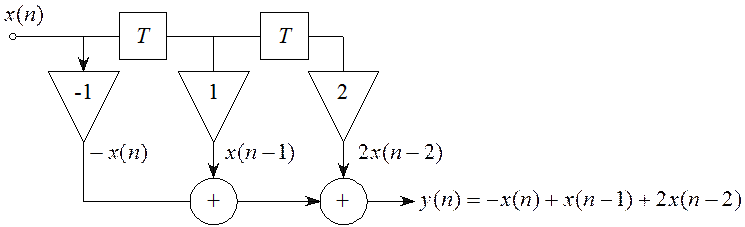
Таким образом, алгоритм вычисления сигнала в рассмотренном выше примере 4.1 будет иметь вид, представленный на рисунке 4.4.

Вывод: В отличие от аналоговых цепей, которые представляют собой соединение элементов , дискретная цепь – это структурная схема вычислений выходной последовательности  по выходной последовательности . Она состоит из элементов задержки, сумматоров и усилителей (умножителей).

Приведенные на рисунке 4.3 операции можно осуществить с помощью элементов цифровой или вычислительной техники. Первые представляют собой выпускаемые промышленностью интегральные микросхемы, позволяющие задерживать, складывать, умножать сигналы. Последние – это серийные макро, микро-ЭВМ, либо микропроцессорные устройства. Характерно, что и те и другие работают с цифровыми сигналами, т.е. с отсчетами, представленными в двоичном коде (0; 1). В этом случае любая конкретная цепь может быть реализована с помощью устройства, собранного на ИМС, либо в виде программы для ЭВМ или микропроцессорного устройства.

Заметим, что представление чисел в двоичном коде из-за ограниченности разрядности цифровых устройств выполняется неточно. Операция умножения отсчетов сигнала на число тоже выполняется неточно из-за округления или усечения результата. Это приводит к ошибкам

Рисунок 4.5

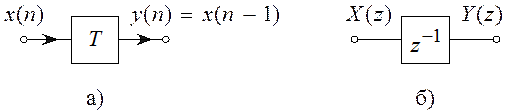
при восстановлении сигнала. Существует только один путь уменьшения этих ошибок – увеличение разрядности устройств обработки.

Вывод: Дискретная цепь – это структурная схема алгоритма вычислений. Цифровая цепь – это воплощение данного алгоритма в виде программных и аппаратных средств.

Рассмотрим один из элементов дискретной цепи – элемента задержки (рисунок 4.5,а). Сигнал на его входе , а на выходе .

Применим Z-преобразование к этим сигналам: ;  – согласно теореме задержки, т.о. .

На рисунке 4.5,б изображено Z-изображение элемента задержки на один интервал дискретизации.

4.3 Передаточная функция дискретной цепи

Передаточной (системной) функцией дискретной цепи  называют отношение Z-преобразований входного и выходного дискретных сигналов

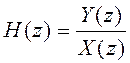                                              (4.3)

Обратимся к теореме свертки, согласно которой свертка дискретных функций  и  соответствует произведение их Z-преобразований, т.е.

Рисунок 4.6                                                               Рисунок 4.7

 

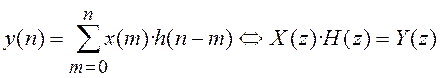
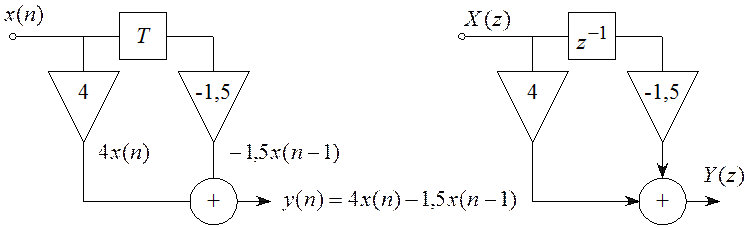
Из последнего выражения видно, что Z-преобразование импульсной характеристики цепи  и есть передаточная функция дискретной цепи

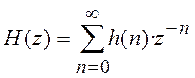                                      (4.4)

Пример 4.2 Найти системную функцию дискретной цепи, имеющей импульсную характеристику .

.

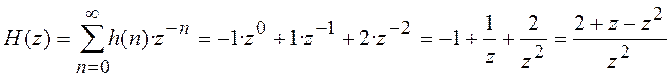Пример 4.3 Найти импульсную характеристику и передаточную функцию дискретной цепи изображенной на рисунке 4.6.

Запишем выражение для выходного сигнала :

Сравним его с выражением, полученным согласно теореме дискретной свертки:

, отсюда ; . Согласно (4.4), передаточная функция

.

Другой способ нахождения  состоит в том, чтобы найти Z-изображение выходного сигнала , а затем найти ;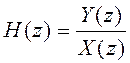

;

.

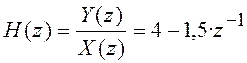Z-изображение дискретной цепи с такой передаточной функцией имеет вид, приведенный на рисунке 4.7.

5 Цифровые фильтры

5.1 Определение и применение цифровых фильтров

Важнейшим примером линейных дискретных систем является линейный цифровой фильтр (ЦФ).

ЦФ называется некоторый алгоритм, который производит определенные операции во временной или частотной области входного дискретного сигнала и формирует выходной дискретный сигнал. Аналогичные действия, но только с непрерывным сигналом, выполняют аналоговые фильтры. При этом ЦФ имеют ряд преимуществ по сравнению с аналоговыми: