Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 27

При обработке сигналов в технике связи возникает ряд задач, связанных с преобразованием спектров сигналов. Некоторые из них решаются с помощью цифровой фильтрации. В отдельную задачу можно выделить задачи, требующие перемещения спектра сигнала по оси частот, например, в многоканальной связи при формировании группового сигнала с частотным разделением каналов или при выделении отдельных канальных сигналов из группового сигнала с ЧРК. При этом амплитудный спектр сигнала практически не меняется. Меняется лишь положение спектра на оси частот. В данной главе рассмотрим цифровые методы переноса спектра сигнала, инверсии спектра и методы формирования спектра с ОБП.

8.2 Перенос и инверсия спектра

Рассмотрим дискретный вещественный сигнал , спектр которого  в полосе нормированных частот  занимает полосу . Модуль спектра сигнала показан на рисунке 8.1,а (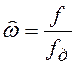 – нормированная частота).

Перенос спектра на оси частот на величину  осуществляется путем умножения отсчетов сигнала  на отсчеты дискретной экспоненты  причем . Действительно, в соответствии с дискретным преобразованием Фурье спектр сигнала  равен

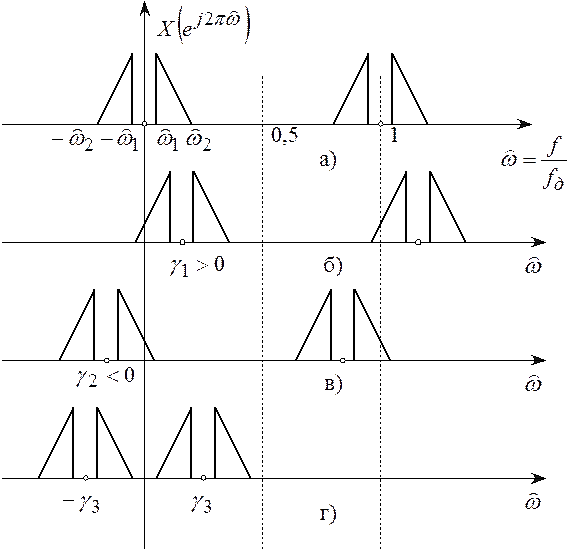
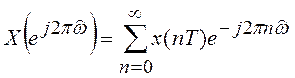                            (8.1)

Умножим сигнал  на дискретную экспоненту . Найдем спектр для сигнала . Он равен

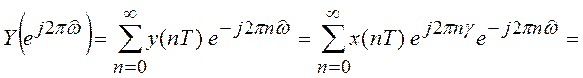
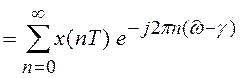                                  (8.2)

Сравнивая (8.1) и (8.2) получим:

                                (8.3)

Из формулы (8.3) видно, что спектр сигнала  представляет собой спектр сигнала , сдвинутый по оси частот на величину .

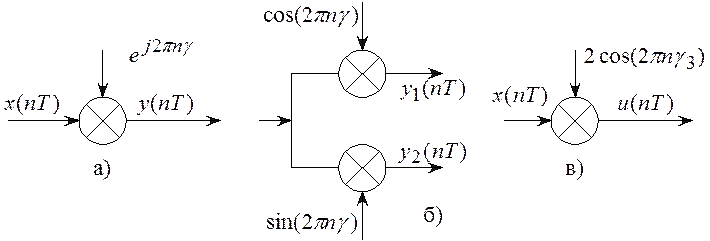
Схема, осуществляющая операцию сдвига, приведена на рисунке 8.2,а. Здесь, правда, нужно не забыть, что умножитель должен выполнять операцию комплексного умножения отсчетов входного сигнала  на отсчеты комплексной экспоненты  и выходной сигнал  в общем случае будет комплексным. Фактически сдвиг спектра осуществляется схемой приведенной на рисунке 8.2,б.

Выходные сигналы  и   представляют собой вещественную и мнимую составляющие комплексного выходного сигнала .

Рассмотрим теперь, как влияют величина и знак параметра  на сдвиг спектра исходного сигнала. Если , спектр сдвигается по оси частот вправо (рисунок 8.1,б). Если , то спектр сдвигается по оси частот влево (8.1,в).

В рассмотренных выше случаях выходной сигнал  является комплексным. Это видно из рисунка модуля спектра (он несимметричен относительно ). Часто возникает задача формирования вещественного сигнала , спектр которого  представляет собой спектр исходного сигнала  с боковыми частотами, расположенными симметрично относительно определенной частоты , . Для получения такого сигнала необходимо умножить отсчеты входного сигнала  на отсчеты дискретной косинусоиды  (схема на рисунке 8.2,в). Действительно,         . В этом случае спектр  сдвинут вправо на , а спектр  влево на  и сигнал  имеет требуемы симметричный относительно нуля спектр 8.1,г, т.е. сигнал  является вещественным.

Важное значение в ряде задач ЦОС играет операция инверсии спектра. Суть операции инверсии состоит в том, что в основной полосе частот спектр как бы “переворачивается”, т.е. определенная частота исходного спектра  оказывается расположенным на частота  (рисунок 8.3,б).

Из рисунка 8.3 хорошо видно, что инверсный спектр получается из исходного сигнала путем сдвига последнего по оси частот на , при этом

.

Для того, чтобы сдвинуть спектр сигнала на величину , нужно умножить отсчеты сигнала  на отсчеты дискретной экспоненты

                 (8.4)

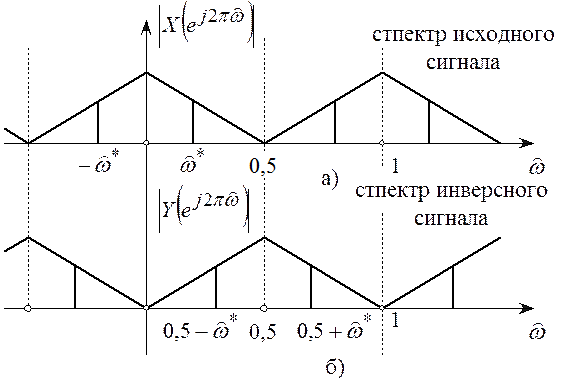
Таким образом, операция инверсии спектра вещественного сигнала  осуществляется путем простого изменения знака каждого его второго отсчета

                      (8.5)

Пример 8.1 Рассмотрим сигнал , где , (например  кГц,  кГц). На рисунке 8.4,а показаны отсчеты сигнала  и для наглядности штриховой линии огибающиеся этого сигнала.