Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 31

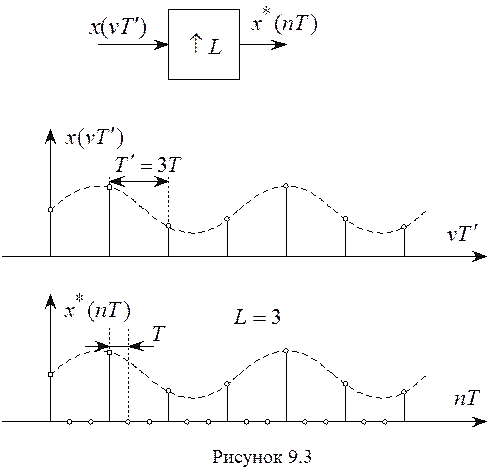
сигнала в нужное число раз L. эту операцию осуществляет эспандер частоты дискретизации (ЭЧД).

Входным сигналом ЭЧД является дискретный сигнал с интервалом дискретизации  (частотой ) , .

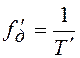Сигнал  преобразуется в сигнал  по алгоритму:

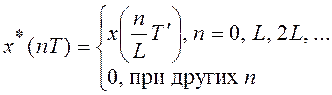
Таким образом формируется выходной дискретный сигнал с интервалом 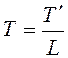дискретизации , который в L раз меньше исходного, или частотой дискретизации 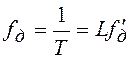 – в L раз больше исходной.

Из рисунка видно, что последовательность  получается из последовательности  путем ввода  нулевых отсчетов между каждой парой отсчетов исходной последовательности. Получим связь между спектром  и . Для этого вначале найдем Z-преобразоваине сигналов  и .

Z-преобразование входной последовательности:

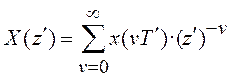,                                     (9.2)

где .

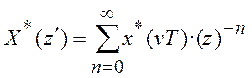,                                     (9.3)

где .

Поскольку , то очевидно, что .

Преобразуем теперь (9.3) учтя, что  для

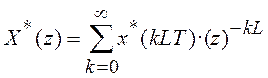.                                  (9.4)

Если учесть, что , а  и, следовательно, , то сравнив (9.4) с (9.2), получим:

                                              (9.5)

Это означает, что Z-преобразование входного и выходного сигналов ЭЧД тождественны.

Соотношения для спектров получим из (9.5), подставив вместо  и

 или

где 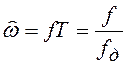 – нормированная частота.

Таким образом, выходной сигнал ЭДЧ , формируемый из входного  по алгоритму (9.1) имеет тот же спектр, что и входной сиг-

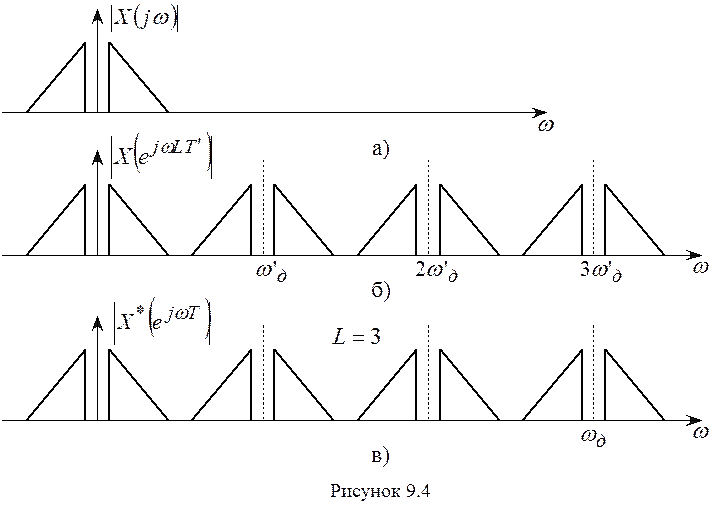
нал.

На рисунке 9.4 показаны спектры модулей входного и выходного сигналов ЭДЧ при .

Внимание: спектр выходного сигнала ЭЧД периодичен со “старой” частотой дискретизации 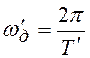, а не с “новой” частотой , как это обычно имеет место для сигналов, интервал дискретизации которых равен Т.

9.4 Простейшая система интерполяции с целочисленным коэффициентом L

Простейшая система повышения частоты дискретизации сигнала в целое число раз L показана на рисунке 9.5,а.

Входным сигналом является сигнал ,  с интервалом дискретизации . Предполагается, что сигнал  с ограниченным спектром занимает полосу частот от . Частота дискретизации

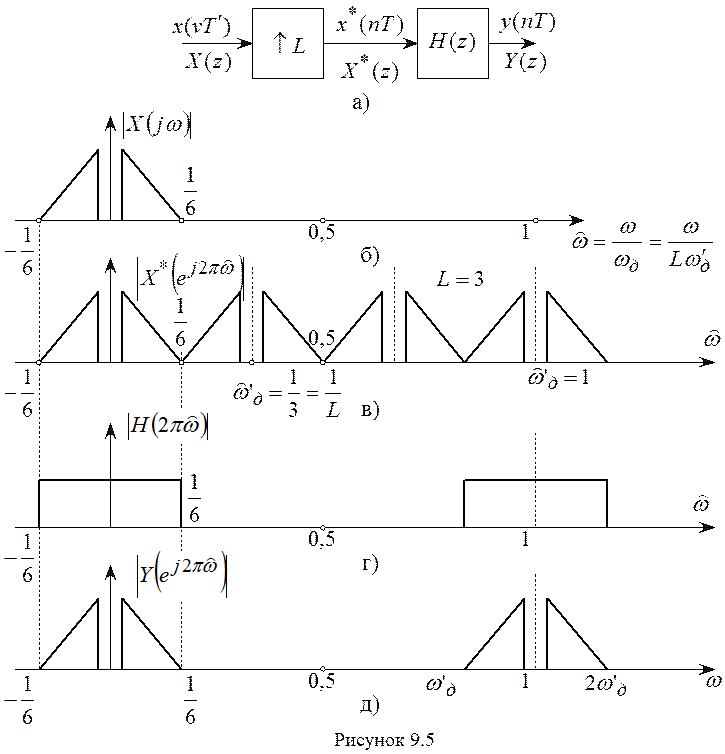
. На рисунке 9.5 показаны модули спектров сигналов  и , на нормированной оси частот 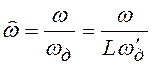 для случая  .

Входной сигнал  поступает на экспандер частоты дискретизации, осуществляющий предварительное увеличение частоты дискретизации в L-раз по алгоритму (9.1):

.

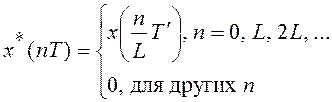Спектры входного и выходного сигналов ЭДЧ равны и периодичны с частотой .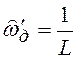

Выходной сигнал ЭДЧ обрабатывается "идеальным" цифровым фильтром НЧ с передаточной функцией  и импульсной характеристикой , задачей которого является подавление “лишних” частотных составляющих спектра , занимающих область частот . Частотные характеристики фильтра должны удовлетворять условию:

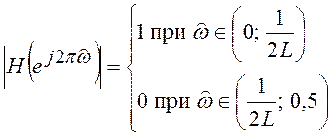                            (9.6)

В качестве ФНЧ могут быть использованы как КИХ так и БИХ-фильтры. КИХ-фильтры позволяют достаточно просто строить эффективные системы преобразования частоты дискретизации сигналов. Как известно, КИХ фильтры имеют передаточную функцию

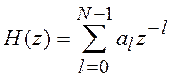                                          (9.7)

и линейную ФЧХ . Они могут иметь нечетное (КИХ-фильтры 1-го вида) и четное (КИХ-фильтры 2-го вида) число отсчетов N импульсной характеристики .

Для фильтров 1-го вида (N – нечетное) 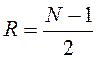 – целое число. Поскольку величина R определяет задержку числа во временной области, вносимую фильтром при обработке сигнала, то задержка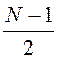 равна целому числу интервалов дискретизации Т. При этом процесс интерполяции по схеме рисунка 9.7 соответствует варианту 1, т.е. увеличение частоты дискретизации осуществляется в соответствии с математическим понятием интерполяции, когда сохраняются отсчеты входного сигнала, модуль спектра и форма огибающей входного сигнала. Для КИХ-фильтров 2-го вида (N – четное) 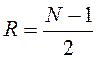 – нецелое число. Процесс интерполяции в этом случае соответствует варианту 2, когда сохраняются и модуль спектра и форма огибающей входного сигнала, но не сохраняются его отсчеты.