Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 26

Если фильтр реализован на специальном микропроцессоре типа DSP, то коэффициенты фильтра фиксируются в виде двоичных кодов с заранее определенным числом  двоичных разрядов. Для DSP . Таким образом, необходимо определить существует ли фильтр, удовлетворяющий условиям задачи, и, если он существует, рассчитать округленные коэффициенты этого фильтра.

Таким образом, на первом этапе определяется фильтр минимального порядка , удовлетворяющий требованиям . На втором этапе рассчитанные коэффициенты округляются до  двоичных разрядов. На третьем этапе рассчитываются минимальные погрешности аппроксимации  и  соответственно в полосе пропускания и полосе задерживания путем вычисления , где  рассчитывается по округленным коэффициентам . На четвертом этапе проверяется условие получения решения.

Если рассчитанные погрешности  и  одновременно не больше заданных допустимых погрешностей  и , то решение определено, и округленные коэффициенты можно использовать для реализации фильтра. Дальнейшие вычисления прекращаются.

Если рассчитанные погрешности превышают допустимую хотя бы в одной полосе, то проверяют условия , где  – неокругленный старший коэффициент передаточной функции. Если условие не выполняется, то можно попытаться увеличить порядок фильтра и тем самым уменьшить погрешность аппроксимации  и . После чего снова решается задача аппроксимации для нового порядка фильтра.

Если же условие  выполняется, то решения нет, т.е. по заданны условиям нельзя построить нерекурсивный фильтр с разрядностью коэффициентов

7.5 Предельные циклы

Ошибки округления при вычислении в ЦФ могут приводить еще к одной серьезной неприятности – появлению так называемых предельных циклов, когда вроде бы устойчивый фильтр начинает демонстрировать неустойчивое поведение. Поясним это явление на простейшем примере. Пусть имеется рекурсивный ЦФ первого порядка, описываемый разностным уравнением

.

Единственный полюс передаточной функции данного фильтра 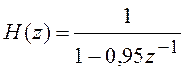 равен 0,95. Он находится внутри единичной окружности, что свидетельствует об устойчивости фильтра. Пусть входной сигнал отсутствует (), а внутреннее состояние фильтра, которое в данном случае представляется единственным числом  равно 13.

При точных вычислениях сигнал на выходе фильтра затухает:

;

;

;

;

;

…

А теперь, будем считать, что в ячейках памяти фильтра значения хранятся в целочисленном формате и после выполнения умножения используется округление. Выходной сигнал радикально изменится

;

;

;

;

;

…

Итак, выходной сигнал “залипает” на значении 10 и далее не меняется. Это и есть простейший случай предельного цикла.

Различают две разновидности предельных циклов:

-  “зернистые” предельные циклы, когда при отсутствии входного сигнала, значение выходного сигнала затухают, но из-за ошибок округления не доходят до нуля. Именно такой цикл наблюдается в приведенном примере;

-  “переполняющиеся” предельные циклы имеют место в том случае, когда из-за вычислительных погрешностей значения выходного сигнала не затухают, а возрастают, вызывая переполнение.

Таким образом, предельные циклы приводят к появлению ложного сигнала на выходе рекурсивного ЦФ. Ложные сигналы в системах передачи недопустимы, поэтому применяют различные способы борьбы с этим явлением. Можно, например, подмешивать к сигналу на входе цепи псевдослучайную последовательность нулей и единиц на уровне младшего разряда кодовых слов. Но при этом необходимо увеличивать на единицу разрядность регистров, чтобы помехозащищенность сигнала осталась на прежнем уровне.

8 некоторые операции над спектрами сигналов в технике связи

8.1 Общие сведения